Файл: Шпоры переделан.docx

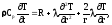(2.6)

где С_р — удельная теплоемкость материала ТВЭЛов; R — удельная ядерная мощность.

8. Типы связей между подсистемами различной физической природы. Ранее были рассмотрены эквивалентные схемы однородных физических подсистем. Но реальный объект представляет собой совокупность разнородных физических подсистем. Согласно основным этапам получения ММС на макроуровне, после составления эквивалентных схем однородных подсистем следует установить связи между ними, т. е. определить их воздействие друг на друга. Можно выделить три типа связей: 1) трансформаторная При трансформаторном типе связи в одной подсистеме включается зависимый источник разности потенциалов. Этот источник зависит от разности потенциалов на зависимом источнике потока, установленном в другой подсистеме, который, в свою очередь, зависит от потока через первый источник. На рис. 10, а показана эквивалентная схема трансформаторной связи, где р и q - подсистемы различной природы. Если же источники в подсистемах поменять местами, то схема будет иметь такой вид, как изображено на рис. 10, б. Подобный вид связи уже встречался в ранее рассмотренных примерах эквивалентных схем однородных физических подсистем (рычаг, зубчатое зацепление колес). Для разнородных физических подсистем рассмотренная выше связь характерна при электромеханическом взаимодействии. 2) гираторная При гираторном типе связи в обеих физических подсистемах включаются зависимые источники одного вида: либо типа разности потенциалов, либо типа тока. Источники разности потенциалов зависят от потока через источник в другой подсистеме (рис. 12, а), источники потока зависят от разности потенциалов на источнике в другой подсистеме (рис. 12, б). Такой вид связи характерен при взаимодействии механической и гидравлической или пневматической подсистем. 3) через зависимые параметры элементов. ^ Связь через зависимые параметры элементов характерна при взаимодействии с тепловой подсистемой. В зависимости от значений температуры меняются параметры элементов взаимодействующей подсистемы, например вязкость жидкости, значение сопротивления резистора. Обратное влияние на тепловую подсистему учитывается введением в эквивалентную схему тепловой подсистемы зависимых источников теплового потока. При отсутствии массопереноса значение источника определяется мощностью, выделяемой элементом; при наличии массопереноса - переносимой массой. В случае моделирования влияния температуры на работу технических объектов без учета обратного воздействия предполагают, как будет изменяться температура во времени, и переносят эту зависимость на параметры элементов объекта, т. е. делают параметры зависимыми от времени. Аналогично моделируют старение элементов объекта при расчетах надежности.

9. Мм на микроуровне

Особенностью ММ на микроуровне является отражение физических процессов, протекающих в непрерывных пространстве и времени. Типичные ММ на микроуровне — дифференциальные уравнения в частных производных (ДУЧП). В них независимыми переменными являются пространственные координаты и время. С помощью этих уравнений рассчитываются поля механических напряжений и деформаций, электрических потенциалов, давлений, температур и т. п. Возможности применения ММ в виде ДУЧП ограничены отдельными деталями, попытки анализировать с их помощью процессы в многокомпонентных средах, сборочных единицах, электронных схемах не могут быть успешными из-за чрезмерного роста затрат машинного времени и памяти.

.10. ММ на макроуровне

На макроуровне используют укрупненную дискретизацию пространства по функциональному признаку, что приводит к представлению ММ на этом уровне в виде систем обыкновенных дифференциальных уравнений (ОДУ). В этих уравнениях независимой переменной является время t, а вектор зависимых переменных V составляют фазовые переменные, характеризующие состояние укрупненных элементов дискретизированного пространства. Такими переменными являются силы и скорости механических систем, напряжения и силы тока электрических систем, давления и расходы гидравлических и пневматических систем и т. п. Системы ОДУ являются универсальными моделями на макроуровне, пригодными для анализа как динамических, так и установившихся состояний объектов. Модели для установившихся режимов можно также представить в виде систем алгебраических уравнений. Порядок системы уравнений зависит от числа выделенных элементов объекта. Если порядок системы приближается к 10³, то оперирование моделью становится затруднительным и поэтому необходимо переходить к представлениям на метауровне.

12. Общие сведения о моделировании на макроуровне

Использование ММ объекта в виде системы дифференциальных уравнений в частных производных воз­можно только для очень простых технических систем, и даже в этом случае порядок аппроксимирующей алгеб­раической системы уравнений при моделировании в трех­мерном пространстве может достигать 10⁶ и более. Поэтому при моделировании на макроуровне в технической системе выделяются достаточно крупные элементы, кото­рые в дальнейшем рассматриваются в виде неделимой единицы. Непрерывной независимой переменной остает­ся (в сравнении с моделированием на микроуровне) только время. Математической моделью технической си­стемы на макроуровне будет система ОДУ.

Поведение большинства технических подсистем мож­но охарактеризовать с помощью фазовых переменных. Фазовые переменные образуют вектор неизвестных в ММ технической системы. Так, в электрической подсистеме фазовыми переменными являются токи и напряжения, в механической поступательной подсистеме - силы и ско­рости.

Математическую модель системы получают объеди­нением компонентных и топологических уравнений.

Законы функционирования элемента подсистемы (в дальнейшем - просто элемента) задаются компонентны­ми уравнениями, связывающими, как правило, разнород­ные фазовые переменные, относящиеся к данному эле­менту, т. е. компонентные уравнения связывают перемен­ные типа потока с переменными типа потенциала.

Компонентные уравнения могут быть линейными или нелинейными, алгебраическими, обыкновенными диффе­ренциальными или интегральными. Эти уравнения по­лучаются на основе знаний о конкретной предметной об­ласти. Для каждого элемента моделируемого техническо­го объекта должны быть получены компонентные урав­нения. Это может оказаться длительной и трудоемкой процедурой. Но эта процедура выполняется однократно с одновременным накоплением библиотеки подпрограмм моделей элементов.

Компонентные уравнения получают либо теоретиче­ски, либо физическим макетированием, либо математиче­ским моделированием на микроуровне.

Связь между однородными фазовыми переменными, относящимися к разным элементам подсистемы, задает­ся топологическими уравнениями, получаемыми на осно­ве сведений о структуре подсистемы. Для формирования топологических уравнений разработаны формальные ме­тоды. Очевидно, что процедура получения то­пологических уравнений выполняется для каждого моде­лируемого объекта, так как структуры объектов раз­личны.

В САПР целесообразно использовать математические и программные средства, обеспечивающие моделирова­ние всей номенклатуры проектируемых объектов и спо­собные адаптироваться к изменяющимся условиям экс­плуатации. Эти свойства достигаются, если применяемые средства имеют высокую степень универсальности. По­лучению универсальных средств способствует использо­вание аналогий между подсистемами различной физиче­ской природы и между моделирующими их компонент­ными и топологическими уравнениями.

13. Методика получения функциональных моделей

Получение моделей элементов (моделирование элементов) в общем случае — процедура неформализованная. Основные решения, касающиеся выбора вида математических соотношений, характера используемых переменных и параметров, принимает проектировщик. В то же время такие операции, как расчет численных значений параметров модели, определение областей адекватности и др., алгоритмизированы и решаются на ЭВМ. Поэтому моделирование элементов обычно выполняется специалистами конкретных технических областей с помощью традиционных средств экспериментальных исследований и средств САПР.

Методы получения функциональных моделей элементов делят на теоретические и экспериментальные. Теоретические методы основаны на изучении физических закономерностей, протекающих в объекте процессов. Далее происходит определение соответствующего этим закономерностям математического описания, обоснование и принятие упрощающих предположений, выполнение необходимых выкладок и приведение результата к принятой форме представления модели. Экспериментальные методы основаны на использовании внешних проявлений свойств объекта, фиксируемых во время эксплуатации однотипных объектов или при проведении целенаправленных экспериментов.

Несмотря на эвристический характер многих операций моделирования, имеется ряд положений и приемов, общих для получения моделей различных объектов. Достаточно общий характер имеют методика макромоделирования, математические методы планирования экспериментов, а также алгоритмы формализуемых операций расчета численных значений параметров и определения областей адекватности.

14. Метод получения топологических уравнений

Метод, основанный на использовании информации, заключенной в М-матрице (в матрице контуров и сече­ний),— наиболее удобный и общий метод получения то­пологических уравнений.

М-матрица строится на основании ориентированного графа эквивалентной схемы и выбранного для этого графа дерева. Количество столбцов матрицы соответст­вует числу ветвей дерева, а количество строк - числу хорд.

Процедура формирования М-матрицы заключается в следующем: каждая хорда графа поочередно вклю­чается в дерево, при этом образуется замкнутый контур; выполняется обход этого контура в направлении, задан­ном направлением хорды; в строке матрицы, соответст­вующей данной хорде, ставится +1, если направление ветви дерева совпадает с направлением обхода контура, -1, если направление ветви дерева противоположно, О, если ветвь не входит в данный контур.