ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.04.2024
Просмотров: 205
Скачиваний: 0
СОДЕРЖАНИЕ
1. Определение математической модели и математического моделирования
2. Основные этапы математического моделирования
3. Свойства математических моделей
4 Требования к математическим моделям
6. Иерархия мм и формы представления
7. Краевые задачи проектирования
13. Методика получения функциональных моделей
14. Метод получения топологических уравнений
18. Аналогии компонентных уравнений
19. Аналогии топологических уравнений
20. Получение эквивалентных схем технических объектов.
21. Аппроксимация табличных данных. Метод наименьших квадратов.
25. Табличный метод получения математических моделей систем
26. Узловой метод получения математических моделей систем.
29. Методы решения систем линейных и нелинейных алгебраических уравнений.
30. Анализ в частотной области.
31. Сравнение методов конечныx элементов и конечных разностей
33. Математические модели дискретных устройств.
35. Основные сведения из теории массового обслуживания
Сечения дерева специально выбирать не надо. Уравнения для сечений получаются из М-матрицы, для построения которой сечения не привлекаются.
Количество топологических уравнений равно количеству ветвей эквивалентной схемы.
15. Метод конечных элементов
В настоящее время метод конечных элементов (МКЭ) является одним из наиболее популярных методов решения краевых задач в САПР. В математическом отношении метод относится к группе вариационно-разностных. Строгое доказательство таких важных свойств, как устойчивость, сходимость и точность метода, проводится в соответствующих разделах математики и часто представляет собой непростую проблему.
Тем не менее МКЭ активно развивается, с его помощью без строгого математического обоснования используемых приемов успешно решаются сложные технические проблемы. Правильность же работы созданных алгоритмов и программ, реализующих МКЭ, проверяют на известных точных решениях. Начав развиваться как метод решения задач строительной механики, МКЭ быстро завоевал такие сферы инженерной деятельности, как проектирование самолетов и автомобилей, космических ракет, тепловых и электродвигателем, турбин, теплообменных аппаратов и др.
К основным преимуществам МКЭ относят доступность и простоту его понимания и применимость метода для задач с произвольной формой области решения, возможность создания на основе метода высококачественных универсальных программ для ЭВМ.
В МКЭ исходная область определения функции разбивается с помощью сетки, в общем случае неравномерной, на отдельные подобласти — конечные элементы. Искомая непрерывная функция аппроксимируется кусочно-непрерывной, определенной на множестве конечных элементов. Аппроксимация может задаваться произвольным образом, но чаще всего для этих целей используются полиномы, которые подбираются так, чтобы Обеспечить непрерывность искомой функции в узлах на границах элементов.
16. Метод конечных разностей
Метод конечных разностей исторически начал развиваться раньше МКЭ и является старейшим методом решения краевых задач.
Алгоритм МКР состоит из этапов, традиционных для метода сеток:
Этап 1. Построение сетки в заданной области. В МКР используется сетка, задаваемая конечным множеством узлов. В узлах сетки определяются приближенные значения φh искомой функции φ. Совокупность узловых значений φh называют сеточной функцией.
Этап
2. Замена дифференциального оператора
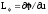 в
исходном дифференциальном уравнении
разностным
аналогом Lh
, построенным по одной из схем рассмотренных
ниже. При этом непрерывная функция φ
аппроксимируется сеточной функцией
φh.
в
исходном дифференциальном уравнении
разностным
аналогом Lh
, построенным по одной из схем рассмотренных
ниже. При этом непрерывная функция φ
аппроксимируется сеточной функцией
φh.
Этап 3. Решение полученной системы алгебраических уравнений.
При кажущейся простоте алгоритма МКР его практическая реализация наталкивается на ряд трудностей. Для выяснения их природы целесообразно рассмотреть основные этапы МКР более подробно.
Построение
сетки в заданной области.
В МКР
используются,
как правило, регулярные сетки, шаг
которых
либо постоянен, либо меняется по
несложному закону.
Примеры построения сеток в МКР даны на
рис.
1.15.
Для
одномерных областей построение сетки
мало
чем отличается от аналогичной процедуры
в МКЭ. Отрезок
длиной L
разбивается
на N
частей
(рис. 1.15, а). Расстояние между двумя
соседними узлами называется шагом
сетки
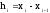 при
i=l,
2, ..., N.
при
i=l,
2, ..., N.
При регулярной сетке шаг hi — постоянная величина, равная 1/(N—1), где N — количество узлов сетки.
17. Метод граничных элементов
Метод Граничных Элементов - это вычислительный метод решения дифференциальных уравнений в частных производных, которые формулируются в виде интегральных уравнениях (граничных интегральных уравнений). Он применяется во многих областях инженерии и науки, включая механику жидкости и газа, акустику, электромагнетизм. МГЭ в определенных случаях оказывается более эффективным в смысле вычислительных ресурсов, чем другие методы, включая Метод Конечных Элементов (МКЭ). В МГЭ рассматривают систему уравнений, включающую только значения переменных на границах области. Схема дискретизации требует разбиения лишь поверхности, а не всей области (отсюда и название метода), так что область становится одним сложным большим “элементом” (в смысле МКЭ). Очевидно, что дискретизация границы порождает меньшую систему общих уравнений задачи, чем дискретизация всего тела. Таким образом, МГЭ уменьшает размерность исходной задачи на единицу, т. е. для трехмерных задач получаются двумерные граничные элементы на поверхности. Применение МГЭ обычно приводит к плотно заполненным матрицам. Это означает, что требования к ресурсам памяти и время вычисления будут расти пропорционально квадрату размера задачи. В то время как, матрицы в МКЭ более разряжены, так как элементы соединены только локально, и требования к ресурсам памяти растут линейно с ростом размера задач. Техники компрессии, например мультипольное разложение (Быстрый Метод Мультиполей, БММ) могут быть использованы для решения этой проблемы, правда ценой повышения сложности программирования. В Центре МГЭ применяется для развития эффективных вычислительных методов и средств для прямого математического моделирования дисперсных систем. Ускорение вычислений МГЭ достигается применением БММ и использованием графических процессоров. Развиваемые программные продукты способны производить прямое моделирование десятков тысяч капель в потоке эмульсии.
18. Аналогии компонентных уравнений
В большинстве технических систем можно выделить три типа простейших элементов:
A. Элемент типа R - элемент диссипации энергии. На этом элементе, как правило, происходит преобразование энергии в тепловую.
Б. Элемент типа С.
B. Элемент типа L.
На элементах типа С и L происходит накопление потенциальной или кинетической энергии.
Сочетанием этих простейших элементов, а также источников фазовых переменных может быть получена ММ технического объекта практически любой сложности.
Рассмотрим основные физические подсистемы с точки зрения аналогий компонентных уравнений.
Для каждой физической подсистемы характерны свои законы, однако для простейших элементов форма выражающих их уравнений оказывается одинаковой.
Электрическая подсистема. Фазовыми переменными электрической подсистемы являются токи I и напряжения U. Запишем уравнения трех типов простейших элементов:
A. Уравнение сопротивления (закон Ома) I=U/R, где R - электрическое сопротивление.
Б. Уравнение емкости I=C(dU/dt), где С - электрическая емкость.
B. Уравнение индуктивности U=L(dI/dt), где L - электрическая индуктивность.
Механическая поступательная подсистема. Фазовые переменные механической поступательной подсистемы - силы F и скорости V - соответственно аналоги токов и напряжений.
Механическая вращательная подсистема. Фазовые переменные этой подсистемы - моменты сил М и угловые скорости ω- соответственно аналоги токов и напряжений.
Гидравлическая (пневматическая) подсистема. Фазовые переменные гидравлической подсистемы - массовые расходы Qm и давления Р - соответственно аналоги токов и напряжений
Тепловая подсистема. Фазовые переменные этой подсистемы - тепловые потоки Ф и температура Т - соответственно аналоги токов и напряжений.
19. Аналогии топологических уравнений
Топологические уравнения в большинстве физических подсистем базируются на уравнениях равновесия и уравнениях непрерывности.
Рассмотрим аналогии топологических уравнений в различных физических подсистемах по отношению к электрической подсистеме.
Электрическая подсистема. Связи между отдельными элементами этой подсистемы устанавливаются на основе законов Кирхгофа.
Уравнение
первого закона Кирхгофа устанавливает
равенство нулю суммы токов в узлах
схемы, т. е.
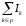 = 0 (уравнение равновесия), гдеIk
–
ток k-й
ветви; р - множество номеров ветвей,
инцидентных рассматриваемому узлу.
= 0 (уравнение равновесия), гдеIk
–
ток k-й
ветви; р - множество номеров ветвей,
инцидентных рассматриваемому узлу.
Из
уравнения второго закона Кирхгофа
видно, что сумма падений напряжений на
элементах схемы при их обходе по
произвольному контуру равна нулю, т. е.
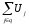 =
0 (уравнение непрерывности), гдеj
- номер ветви; Uj
-
падение напряжения на j-й
ветви схемы, входящей в контур; q
здесь
и далее - множество номеров ветвей,
входящих в рассматриваемый контур.
=
0 (уравнение непрерывности), гдеj
- номер ветви; Uj
-
падение напряжения на j-й
ветви схемы, входящей в контур; q
здесь
и далее - множество номеров ветвей,
входящих в рассматриваемый контур.
Механическая
поступательная подсистема. Аналогом
уравнения первого закона Кирхгофа
является уравнение принципа Даламбера:
сумма сил, действующих на тело, включая
инерционные, равна нулю, т. е.
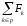 =
0, где Fk
-
сила, приложенная к телу.
=
0, где Fk
-
сила, приложенная к телу.
Аналогом
уравнения второго закона Кирхгофа будет
уравнение принципа сложения скоростей:
абсолютная скорость является суммой
относительной и переносных скоростей,
или же сумма этих трех скоростей равна
нулю (переносных скоростей может быть
несколько: с первого тела на второе, со
второго на третье и т. д.), т. е.
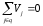
Для механических плоскостных и пространственных систем рассмотренные принципы применимы, если Fk и Vj представить в виде векторных величин, когда приведенные выше уравнения справедливы для каждой координатной оси, например для пространственных систем
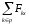 =0;
=0;
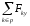 =0;
=0;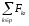 =0;
=0;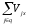 =0;
=0;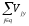 =0;
=0;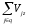 =0;
=0;
где Fkx, Fky, Fkz - соответственно проекции сил на оси х, у, z; Vjx, Vjy, Vjz - соответственно проекции скорости на оси х, у, z.
Механическая
вращательная подсистема. Аналогом
уравнения первого закона Кирхгофа
является уравнение принципа Даламбера
для вращательных подсистем, т. е.
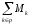 =
0,
где Мk
-
момент
силы,
действующий относительно оси вращения,
включая момент, вызванный моментом
инерции.
=
0,
где Мk
-
момент
силы,
действующий относительно оси вращения,
включая момент, вызванный моментом
инерции.