ВУЗ: Новосибирский государственный технический университет
Категория: Учебное пособие
Дисциплина: Основы теории управления
Добавлен: 15.02.2019
Просмотров: 1438
Скачиваний: 4
2. Для каждой -й трапеции находится коэффициент
i
χ
ω
ω
i
di
Пi
=
(в примере
).
i
= 1 2 3
, ,
3. По таблице h-функций для определенного значения
χ
i
, задаваясь временем
τ
от 0 до
τ
i
(установившееся значение) определяются
h
i
i
( )
τ
, (в примере
i
= 1 2 3
, ,
).
4. По теореме об изменении масштаба по оси ординат, от единичной трапеции переходят к
реальным.
x
h
P
i
i
i
i
( )
( )
( )
τ
τ
=
⋅
0
, (в примере
i
= 1 2 3
, ,
)
5. По теореме об изменении масштаба по оси абсцисс, переходят к реальному времени
.
t
=
Пi
i
i
i
x
t
x
ω
τ
)
(
, (в примере
i
= 1 2 3
, ,
)
6. Результирующий ПП равен алгебраической сумме ПП для отдельных трапеций
x t
x t
i
i
( )
( )
=
=
∑
1
, (в примере
i
= 1 2 3
, ,
)
Кроме рассмотренного метода трапеций применяется ещё метод треугольников. Он отличается от
рассмотренного тем, что разбиение ВЧХ производится не на трапеции, а на треугольники, т.е.
исключается еще один параметр
χ
. Таблицы h-функций для треугольников несколько проще, однако он
широко не распространён из-за большого количества треугольников, аппроксимирующих кривую ВЧХ.
Связь ВЧХ замкнутой системы с амплитудно-фазовой характеристикой
разомкнутой системы (круговые диаграммы)
Установим связь между кривой АФХ разомкнутой системы и
ВЧХ замкнутой. С этой целью на график АФХ разомкнутой
системы наносят сетку кривых одинаковых значений
P( )
ω
,
называемую вещественной круговой диаграммой.
X(p)
G(p)
W
p
(p)
рис. 103
E(p)
Если имеем САУ (рис.103)
W j
M
jN
p
(
)
( )
( )
ω
ω
ω
=
+
,
(1)
W j
W j
W j
P
jQ
з
p
p
(
)
(
)
(
)
( )
( )
ω
ω
ω
ω
ω
=
+
=
+
1
.
(2)
Подставим (1) в (2), получим
.
)
(
)]
(
1
[
)]
(
)
(
)
(
1
)][
(
[
)
(
)]
(
1
[
)
(
)
(
)
(
1
)
(
)
(
)
(
)
(
2
2
2
)]
(
)
(
1
[
)]
(
)
(
1
[
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
N
M
N
M
M
N
j
N
M
M
jN
M
jN
M
jQ
P
jN
M
jN
M
+
+
−
+
+
+
+
⋅
=
=
+
+
+
=
+
−
+
⋅
−
+
⋅
(3)
Приравниваем в (3) вещественные части, получим
P
M
M
N
M
N
M
M
N
M
N
( )
( )[
( )]
( )
[
( )]
( )
( )
( )
( )
[
( )]
( )
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
=
+
+
+
+
=
+
+
+
+
1
1
1
2
2
2
2
2
2
2
ω
.
(4)
Уравнение (4) при
P
const
( )
ω
=
в координатной системе
[ ( ), ( )]
M
N
ω
ω
является уравнением
окружности. Покажем это: Из (4) получаем
P
P
M
P
M
P
N
M
M
N
( )
( ) ( )
( )
( )
( )
( )
( )
( )
( )
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
+
+
+
−
−
−
2
0
2
2
2
2
=
(5)
или
M
P
M
P
N
P
P
2
2
1
2
1
1
( )[ ( )
]
( )[
( )
]
( )[ ( )
]
( )
ω
ω
ω
ω
ω
ω
ω
− +
− +
− = −
.
(6)
Разделим левую и правую части (6) на
[ ( )
]
P
ω
− 1
M
M
P
P
N
P
P
2
2
2
1
1
1
( )
( )
( )
( )
( )
( )
( )
ω
ω
ω
ω
ω
ω
ω
+
−
−
+
= −
−
.
(7)
65
Добавим к левой и правой частям (7) многочлен
[
( )
]
[ ( )
]
2
1
4
1
2
2
P
P
ω
ω
−
−
2
2
2
2
2
2
]
1
)
(
[
4
]
1
)
(
2
[
1
)
(
)
(
)
(
]
1
)
(
[
4
]
1
)
(
2
[
1
)
(
1
)
(
2
)
(
)
(
−
−
+
−
−
=
+
−
−
+
−
−
+
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
P
P
P
P
N
P
P
P
P
M
M
,
M
P
P
N
P
P
P
P
( )
( )
[ ( )
]
( )
( )
( )
[
( )
]
[ ( )
]
ω
ω
ω
ω
ω
ω
ω
ω
+
−
−
+
= −
−
+
−
−
2
1
2
1
1
2
1
4
1
2
2
2
2
.
(8)
Уравнение (8) в координатах
[ ( ), ( )]
M
N
ω
ω
при
P
const
( )
ω
=
представляет собой окружность с
радиусом
2
2
2
2
2
2
2
2
2
]
1
)
(
[
4
1
]
1
)
(
[
4
1
)
(
4
)
(
4
)
(
4
)
(
4
]
1
)
(
[
4
]
1
)
(
2
[
]
1
)
(
2
)[
(
4
]
1
)
(
[
4
]
1
)
(
2
[
1
)
(
)
(
−
=
−
+
−
+
+
−
=
=
−
−
+
−
−
=
−
−
+
−
−
=
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
P
P
P
P
P
P
P
P
P
P
P
P
P
P
R
(9)
или
R
P
=
−
1
2
1
[ ( )
]
ω
.
(10)
Центр окружности расположен на вещественной оси M на расстоянии
l
P
P
= −
−
−
2
1
2
1
( )
[ ( )
]
ω
ω
от начала
координат.
ω
1
ω=0
Рис.104
N( )
ω
Im
Im
M( )
ω
-1,j0
-0
,5
-1,0
-0
,2
0,2
0,3
0,4
0,5
0,6
0,65
0,7
0,75
0,8
0,9
0,8
5
0,0
0,1
ω
2
ω
3
ω
4
ω
5
ω
6
ω
7
ω
8
-5
-4
-3
-2
0
-1
1
2
3
4
-2
-3
-4
1
2
3
4
5
1,1
1,0
1,15
1,2
1,25
1,3
1,35
1,4
1,5
1,6
1,7
1,8
1,9
2,
0
2,
2
2,
5
3,
0
P
R
l
( )
;
, ;
, .
ω
=
=
= −
0
0 5
0
P
R
l
( )
, ;
;
.
ω
=
=
= −
1 5
1
2
5
P
R
( )
, ;
;
.
l
ω
=
=
0 5
1
0
=
P
R
l
( )
, ;
, ;
, .
ω
=
=
= −
2 0
0 5
1 5
P
R
l
п я
( )
, ;
;
( р
)
мая .
ω
=
= ∞
= ∞
1 0
66

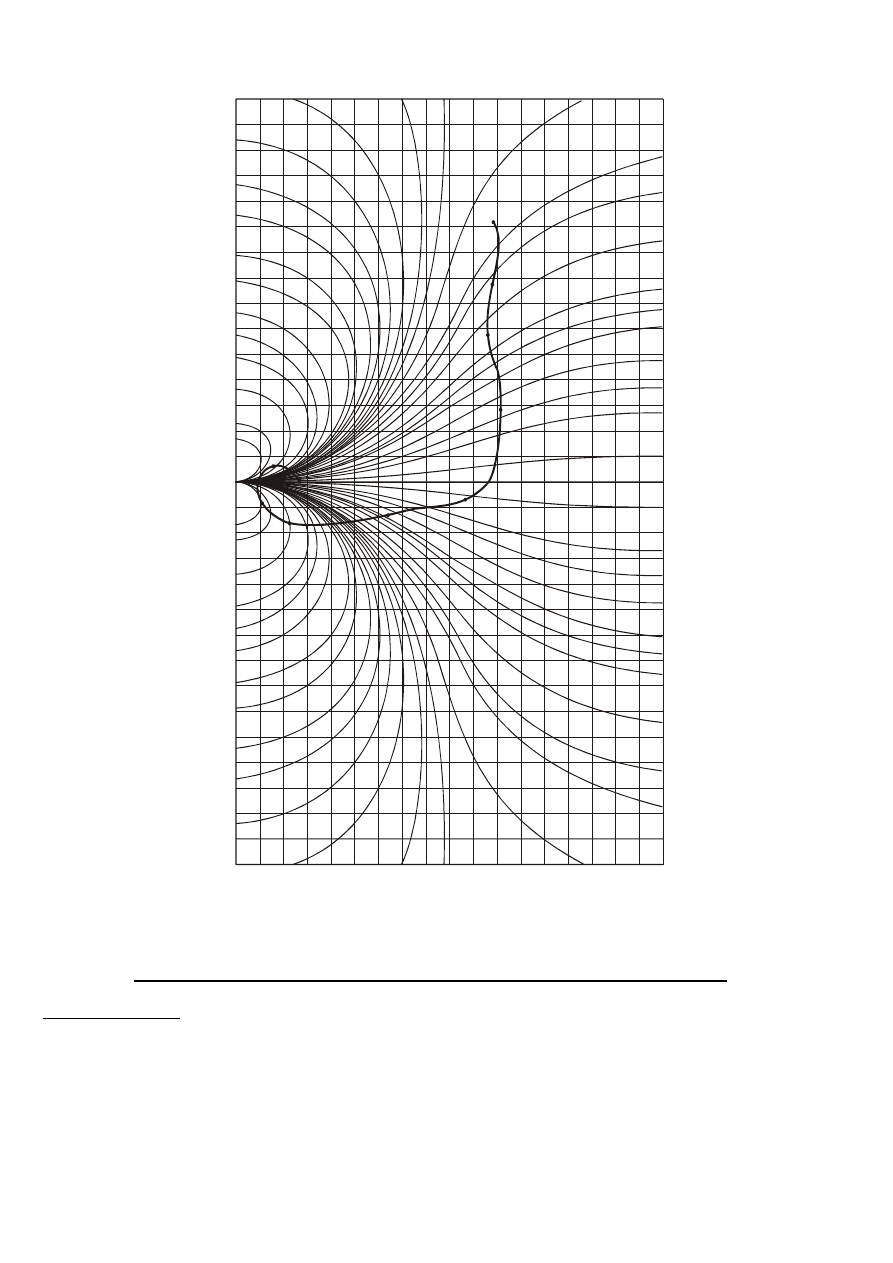
Для определения графика
P( )
ω
замкнутой
системы, на круговую диаграмму, взятую из
литературы (рис.104), необходимо наложить
АФХ разомкнутой системы, вычерченную на
кальке в том же масштабе. Точки пересечения
АФХ
с
окружностями
P const
=
будут
определять
ординаты
P( )
ω
при
ω
,
соответствующих точкам пересечения (рис.105).
P
ω
ω
1
ω
2
ω
3
ω
4
ω
5
ω
6
ω
7
ω
8
0,5
0,4
0,3
0,2
0,1
-0,1
-0,2
-0,3
-0,4
-0,5
0,6
0,7
0,8
Рис.105
Аналогичным образом может быть построена мнимая круговая диаграмма для
.
Q const
=
Отметим, что круговыми диаграммами для построения ВЧХ замкнутой системы по АЧХ
разомкнутой системы можно пользоваться только для систем с единичной обратной связью.
Определение ВЧХ замкнутой системы по ЛЧХ разомкнутой системы
Если расчет устойчивости САУ производился по ЛЧХ, то аналогично выше рассмотренному, на
плоскости ЛАФЧХ разомкнутой системы можно построить диаграммы с линиями равных
P
(или
) и
определить ВЧХ (или МЧХ) замкнутой системы.
Q
Если
W j
A
e
A
jA
p
j
(
)
( )
( ) cos ( )
( ) sin ( )
( )
ω
ω
ω
ϕ ω
ω
ϕ
ϕ ω
=
=
+
ω
,
(1)
то
W j
W j
W j
A
jA
A
jA
з
p
p
(
)
(
)
(
)
( ) cos ( )
( ) sin ( )
( ) cos ( )
( ) sin ( )
ω
ω
ω
ω
ϕ ω
ω
ϕ ω
ω
ϕ ω
ω
ϕ ω
=
+
=
+
+
+
1
1
.
(2)
Выделив из (2) вещественную и мнимую части, получим
P
A
A
A
A
( )
( )
( ) cos ( )
( )
( ) cos ( )
ω
ω
ω
ϕ ω
ω
ω
ϕ
=
+
+
+
2
2
1
2
ω
(3)
и
Q
A
A
A
( )
( ) sin ( )
( )
( ) cos ( )
ω
ω
ϕ ω
ω
ω
ϕ
=
+
+
1
2
2
ω
.
(4)
По уравнениям (3) [или (4)] при
P const
=
(или
Q const
=
) построены диаграммы (номограммы)
(рис. 106).
По известным ЛАХ и ЛФХ разомкнутой системы, для
ω
i
строится на номограмме (на кальке в
масштабе номограммы АФХ) характеристика разомкнутой системы, указывая частоты на ней
ω
i
. По
точкам пересечения этой характеристики с кривыми номограммы определяется вещественная (или
мнимая) частотная характеристика замкнутой системы.
Аналогично предыдущему, номограммами для построения ВЧХ замкнутой системы по ЛЧХ
разомкнутой можно пользоваться только для единичной обратной связи. При неединичной обратной
связи, если есть возможность, то необходимо привести ОС к единичной. Если это не удается, то
круговыми диаграммами и номограммами пользоваться нельзя. В этом случае ВЧХ можно построить по
аналитической зависимости
P( )
ω
замкнутой системы при изменении
ω
от 0 до
∞
.
67
ϕ°(ω)
Рис.106
2
2
0
0
-2
-2
-4
-4
-6
-6
-8
-8
-10
-10
-12
-12
-14
-14
-16
-16
-18
-18
-20
-20
-22
-22
-24
-26
-28
-24
-26
-28
4
4
6
6
8
8
10
10
12
12
14
14
16
16
18
18
20
2
22
22
24
24
26
26
28
28
0
0
20
°
-20
°
40
°
-40
°
60
°
-60
°
80
°
-80
°
100
°
-100
°
120
°
-120
°
140
°
-140
°
160
°
-160
°
180
°
дб
дб
-180
°
0
2,5
3,0
1,8
1,5
1,4
1,3
1,2
1,15
1,10
1,075
1,05
1,03
1,0
1
1,
00
0,9
8
0,95
0,93
0,90
0,85
0,82
0,80
0,75
0,70
0,65
0,59
0,50
0,41
ω
1
ω
2
ω
3
ω
4
ω
5
ω
6
ω
7
ω
8
ω
9
0,35
0,30
0,25
0,20
0,18
0,15
0,10
0,07
0,05
0,02
0,0
-0
,0
1
-0,
03
-0,05
-0,07
5
-0,10
-0,15
-0,20
-0,3
-0,4
-0,5
-0,8
-1,5
-2,0
СИНТЕЗ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Постановка задачи:
Как мы уже говорили, при исследовании САУ приходиться иметь дело с двумя задачами:
1. Задача анализа, когда при заданной САУ требуется определить её устойчивость и построить
переходные процессы, т.е. имеем дело, в основном, с математической задачей.
2. Задача синтеза САУ, когда по заданным показателям качества необходимо определить
параметры САУ.
Обе задачи имеют много общего и связаны между собой. Однако задача синтеза значительно
сложнее задачи анализа, её решение не является однозначным, т.к. одни и те же качественные
показатели можно удовлетворить различными путями.
Рассмотрим структуру САУ.
68
x(t)
g(t)
Регулятор
ε
(t)
Объект
управления
u(t)
f(t)
Рис.107
Синтезировать всю САУ почти невозможно. Поэтому обычно (что практически оправдано) часть
проектируемой системы задано. Обычно задана и выбирается по техническим параметрам силовая часть
системы (объект управления). Кроме того, заданы качественные показатели переходного процесса.
Пэотому необходимо определить параметры регулятора, которые удовлетворяют выше названным
требованиям.
Нередко задача синтеза суживается ещё больше, а именно, при заданном ОУ и регуляторе,
требуемые показатели качества обеспечиваются включением так называемых корректирующих
устройств.
Формулировка задачи синтеза
Правильно поставленная задача синтеза должна содержать три элемента:
1. Задание математической модели объекта.
2. Задание требований к статическим и динамическим свойствам системы.
3. Задание класса регуляторов.
1. Математическая модель объекта, как известно, может быть представлена в виде:
1.1. Системы дифференциальных уравнений. Тогда математическая модель будет описываться
тройкой матриц
{
}
A B C
, ,
;
1.2. Передаточных функций (матриц)
W p
( )
;
1.3. Частотных характеристик системы
W j
P
jQ
(
)
( )
( )
ω
ω
ω
=
+
.
2. В зависимости от выбранной формы описания объекта, требования к статике и динамике системы
могут быть также сформулированы в виде:
2.1. Желаемых матриц
, задающих поведение замкнутой системы;
{
A
B C
*
*
*
,
,
}
2.2. Желаемых передаточных функций (матриц) замкнутой САУ
W p
*
( )
;
2.3. Желаемых частотных характеристик замкнутой системы
W
j
.
*
(
)
ω
Желаемые характеристики во всех трёх случаях определяются исходя из требуемых показателей
качества переходного процесса, т.е.
ε
σ
µ
,
, %,
t
p
.
3. Класс регуляторов задаётся также в зависимости от выбора описания объекта.
Сочетание всех трёх элементов обуславливает выбор метода синтеза системы. В настоящее время
для синтеза линейных систем разработано
≈ 15 методов. Однако наибольшее распространение из них
получили 5 - 6.
При синтезе современных сложных систем управления необходимо проводить анализ с точки
зрения их управляемости, а предъявляемых требований с точки зрения их реализуемости.
Управляемость динамических систем
Это понятие было сформулировано в начале 60-х годов в США Р.Калманом и в настоящее время
является одним из фундаментальных понятий в теории управления.
69