Файл: Конспект лекций СанктПетербург 2011.doc

Анализируя рис. 2.10 можно сделать следующие практически важные выводы:

1. АКФ пачки импульсов существует только на дискретных интервалах времени 2t_и, а в остальной области равна нулю.

2. Огибающая первичных АКФ соответствует АКФ одиночного импульса.

3. Огибающая вторичной АКФ (показана пунктиром) соответствует АКФ прямоугольного импульса длительностью, равной длительности всей пачки.

4. Максимальное значение АКФ в три раза больше, чем максимум АКФ одиночного импульса.

В заключение заметим, что АКФ существуют как для детерминированных, так и для случайных сигналов. Физический смысл АКФ заключается в том, что она дает представление об интегральной скорости изменения сигнала: чем быстрее меняется сигнал, тем ýже АКФ и наоборот.

Большое значение при анализе сигналов имеет взаимная корреляционная функция (ВКФ):
K₁₂() = s₁(t)  s₂(t) = ; (2.8)

K₂₁() = s₂(t)  s₁(t) = . (2.8а)

Здесь s₁(t) и s₂(t) – два различных сигнала.

В отличие от АКФ, взаимная корреляционная функция двух сигналов может не обладать симметрией и иметь максимум при ненулевом сдвиге. Максимальное значение ВКФ численно равно взаимной энергии сигналов.

Физический смысл ВКФ – мера сходства двух сигналов. Чем больше один сигнал похож на другой, тем больше максимум ВКФ.

Таким образом, АКФ является частным случаем ВКФ при s₁(t) = s₂(t).

Характеристики сигналов в области частот – спектральные характеристики – подробно рассматриваются далее.

---

Лекция 3. Сигналы и их спектры

Основы спектрального анализа детерминированных сигналов. Спектральный анализ периодических и непериодических сигналов. Ряд Фурье. Примеры спектров простейших сигналов.
Спектральный анализ радиосигналов основан на разложении по базису ортогональных функций.

В математике понятие ортогональности функций y(x) в общем виде формулируется следующим образом:
при m  n ;

при m = n . (3.1)

Применительно к радиотехнике с физической точки зрения это означает, что некоторые два сигнала обладают ненулевой собственной энергией, но их взаимная энергия равна нулю. Таким образом, при спектральном разложении соблюдается закон сохранения энергии: энергия исходного сигнала равна совокупности энергии спектральных составляющих.

Самый распространенный в радиоэлектронике базис – базис тригонометрических функций (разложение по гармоническим сигналам).

Основные свойства гармонических сигналов, которые обусловливают их применимость:

• 
  условие ортогональности выполняется на интервале, кратном периоду;
  
• 
  форма гармонических сигналов сохраняется при линейных преобразованиях (изменяется только амплитуда и фаза);
  
• 
  возможно использование методов анализа и синтеза, разработанных в электротехнике применительно к синусоидальным колебаниям.
  

В случае периодического исходного сигнала при разложении в спектр получаем бесконечную сумму ряда
s(t) = a₀/2 + [a_ncos(2nf₀t) + b_nsin(2nf₀t)], (3.2)

где a_n и b_n – коэффициенты разложения (спектральные коэффициенты), n – номер гармоники, f₀ – частота первой гармоники.

Выражение (3.2) известно как тригонометрический ряд Фурье. Коэффициент a₀/2 называют постоянной составляющей сигнала.

---

На практике формула (3.2) неудобна, поскольку коэффициенты разложения a_n и b_n не имеют подходящей физической интерпретации.

Учитывая, что любую тригонометрическую функцию можно привести к виду A₀cos(2f₀ + ₀) приведем альтернативную запись тригонометрического ряда Фурье:

s(t) = А₀/2 + [А_ncos(2nf₀t) + _n]. (3.3)

Связь коэффициентов в формулах (3.2) и (3.3):
A_n = , _n = – arctg (b_n /a_n). (3.4)
Физически коэффициенты A_n– это амплитуда, а _n – фаза гармоники. Совокупность спектральных коэффициентов называют спектром сигнала в выбранном базисе.

Коэффициенты спектрального разложения вычисляют по следующим формулам:
a_n = ;

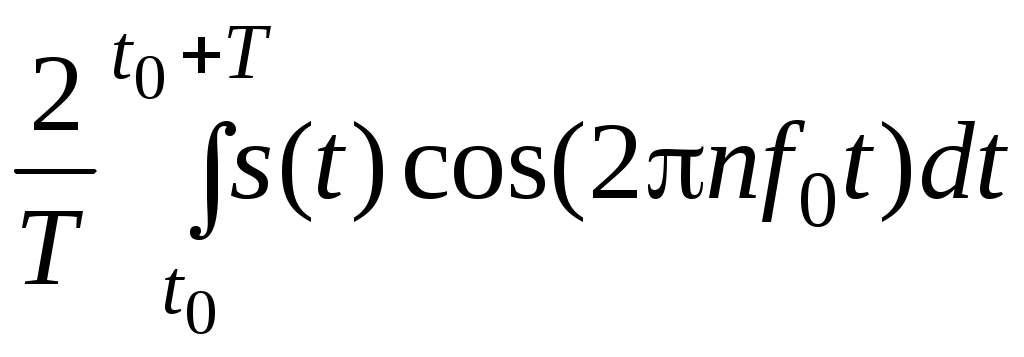b_n = 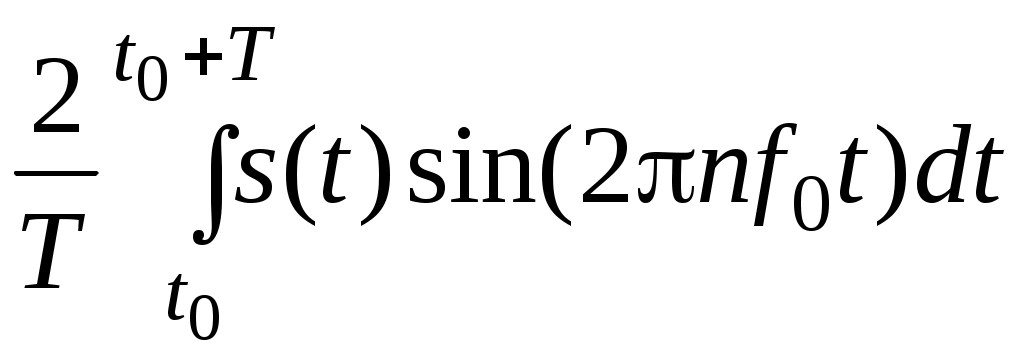, (3.5)
Рассмотрим примеры разложения наиболее часто встречающихся сигналов по гармоникам.

Пример 3.1. Пусть задан исходный периодический сигнал s_п(t) в виде бесконечной последовательности униполярных прямоугольных импульсов (рис. 3.1).

Воспользовавшись формулами (3.4), (3.5) и проведя несложные преобразования, получим

A_n = (2U_mt_и/T_и) ;

_n = 0, , 2 и т.д.
Здесь использована функция sinc (x) = sin(x)/x (рис. 3.2).




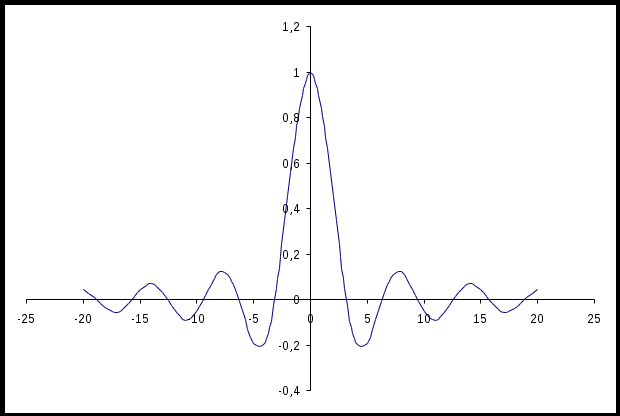
Рис. 3.2
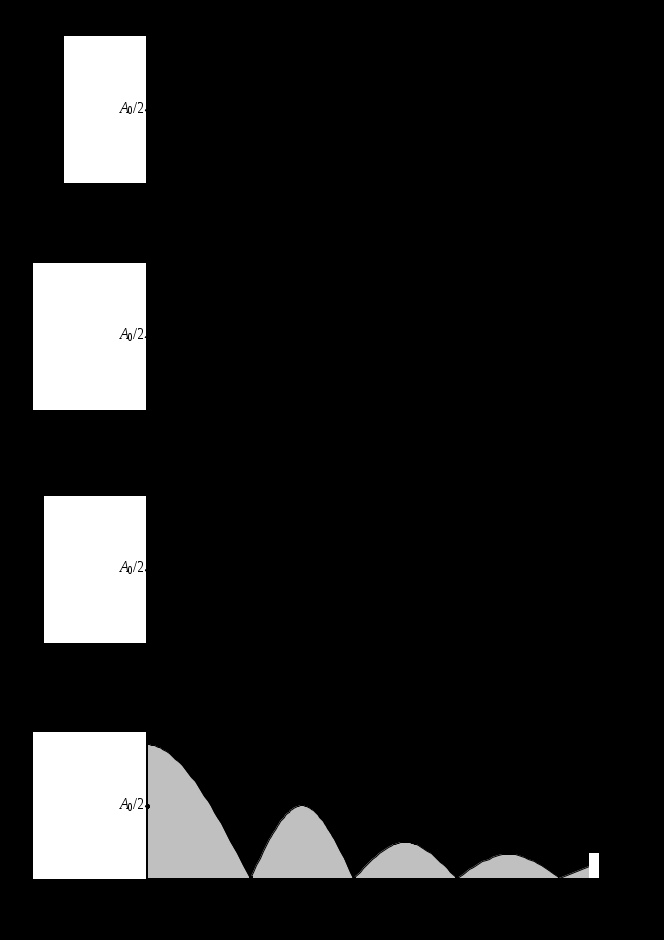
На рис. 3.3 приведено графическое представление спектра амплитуд и фаз рассмотренной последовательности прямоугольных импульсов.


Анализируя рис. 3.3, можно сделать следующие основные выводы:
1. Спектр бесконечной последовательности прямоугольных импульсов бесконечен.
2. При f = 0 имеем амплитуду постоянной составляющей A₀/2.
3. Спектральные составляющие существуют только при определенных дискретных значениях частоты, кратных

---

f₀.
4. Амплитуда спектральных составляющих убывает с ростом частоты по закону функции sinc.
5. При частотах, кратных 1/t_и амплитуда равна нулю.
6. Фаза принимает значения 0, .
Рассмотрим как влияет изменение длительности импульсов и периода их следования на результирующий спектр.
1. Пусть T_и = const, t_и  var. Частоты гармоник не зависят от t_и и остаются постоянными. При увеличении длительности импульсов величина 1/t_и уменьшается, спектр сжимается (рис. 3.4); при уменьшении длительности импульсов спектр растягивается (рис. 3.5). Для наглядности фазы _n не показаны.
2. Пусть t_и= const, T_и  var. Очевидно, что ширина спектра не зависит от T_и и будет неизменной. Изменяется число спектральных составляющих.

Примем для определенности, что период уменьшается, тогда величина 1/T_и растет, а число гармоник уменьшается (рис. 3.6). С ростом T_и насыщенность гармониками возрастает и в пределе при T_и   расстояние между соседними спектральными составляющими стремится к нулю и спектр становится сплошным (рис. 3.7). Попутно заметим, что при T_и   периодическая последовательность превращается в одиночный импульс (непериодический сигнал). Непериодические сигналы и их характеристики будут подробнее рассмотрены в лекции 4.




Пример 3.2. Пусть задан сигнал в виде бесконечной синусоиды с постоянной амплитудой и нулевой начальной фазой (рис. 3.8):
s(t) = U_m sin (2f₀t). (3.6)


Формально сигнал вида (3.6) представить в виде разложения на элементарные математические функции невозможно, поскольку для него не выполняется условие абсолютной интегрируемости. Не вдаваясь в подробности, получим спектральное представление на основе эмпирических соображений.

Сравнивая (3.2) и (3.6) , замечаем, что бесконечная сумма ряда вырождается в единственное слагаемое b₁ sin (2f₀t), следовательно а₀ = а₁ = ... а_n = 0, b₂ = b₃ = = ... b_n = 0, лишь при n = 1, b₁ = U_m.

На оси частот имеем единственную точку с ненулевой амплитудой A₁ при f = f₀ (рис. 3.9).

---

В таком случае считается, что спектр бесконечного синусоидального сигнала с постоянной амплитудой и мгновенной частотой представляет собой одну бесконечно узкую составляющую (единственную гармонику).
Примечание. На самом деле энергия сигнала, рассмотренного в примере 3.2, будет бесконечно велика, поэтому согласно закону сохранения такой же должна быть и энергия спектра. С другой стороны при бесконечной длительности синусоидального сигнала его спектральная составляющая должна иметь бесконечно малую ширину. Это невозможно для элементарных математических функций. Чтобы обойти данное противоречие в радиоэлектронике прибегают к физической абстракции – сигналу в виде -функции Дирака, обладающей бесконечной малой длительностью и бесконечно большой энергией. На рис. 3.9 приведено ее обозначение в виде стрелки с символом .

Пример 3.3. Сигнал представляет собой бесконечную последовательность гауссовых импульсов длительностью t_и, следующих с интервалом Т_и (рис. 3.10).



При построении спектральной диаграммы учтем то обстоятельство, что гауссовому сигналу вида ₁exp(–₁t ²) в частотной области соответствует тоже гауссова функция, но отличающаяся масштабом: ₂exp(–₂ f ²).

Второе эмпирическое правило, помогающее получить спектр данного сигнала, состоит в том, что при переходе от времени к частоте огибающей исходного сигнала будет соответствовать заполнение спектральной диаграммы, а заполнению сигнала – огибающая спектра.

Третье важное правило, сформулированное в примере 3.1, связывает масштаб сигнала и спектра: коротким сигналам соответствуют протяженные спектры и наоборот спектры сигналов с большой длительностью имеют малую ширину.

Таким образом, на оси частот относительно короткому гауссовому импульсу будет соответствовать относительно протяженная гауссова огибающая, а равномерной бесконечной огибающей соответствуют бесконечно короткие -функции заполнения, следующие с интервалом f₀=1/Т_и. Постоянная составляющая будет равна средней мощности сигнала.

В результате амплитудный спектр будет выглядеть так, как показано на рис. 3.11.

---