ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 281
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Лекция 1. Введение в радиоэлектронику
Лекция 2. Сигналы и их временные модели
Лекция 3. Сигналы и их спектры
Лекция 4. Дискретизация сигнала и спектра
Лекция 5. Амплитудно-модулированные колебания
Лекция 6. Колебания с угловой и импульсной модуляцией
Примечание. Знак "+" означает возможность применения данного сигнала
Лекция 7. Линейные радиотехнические цепи
Рассмотрим односторонний экспоненциальный импульс (рис. 4.4).
Вычисление спектральной плотности осуществляем аналогично предыдущему примеру:
= 
=
= 
=
=
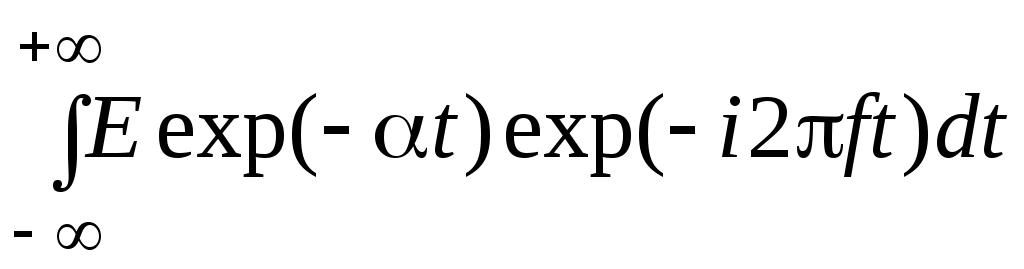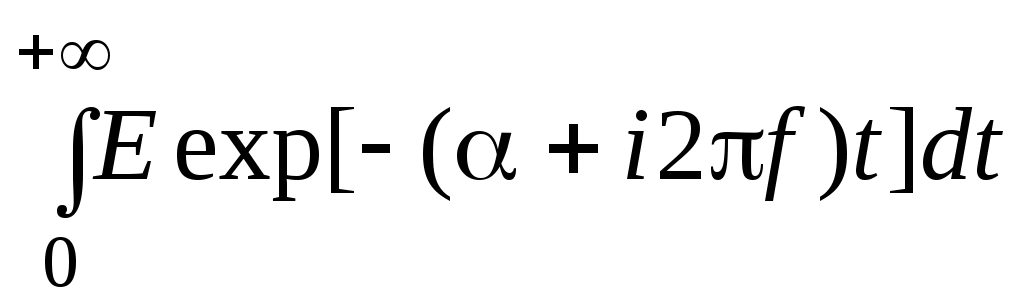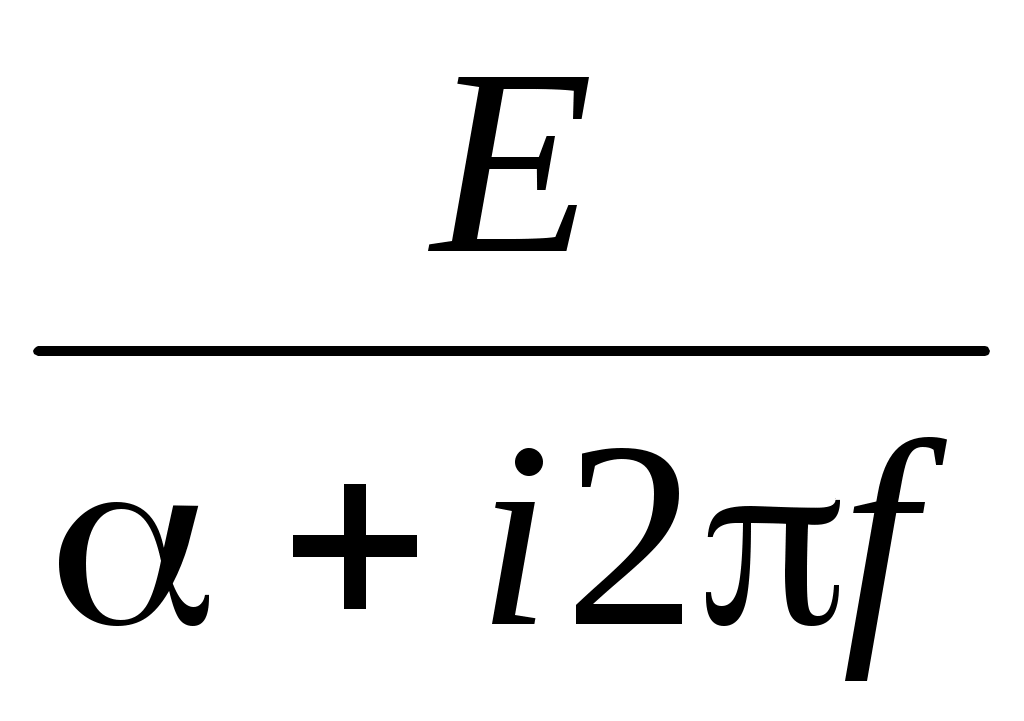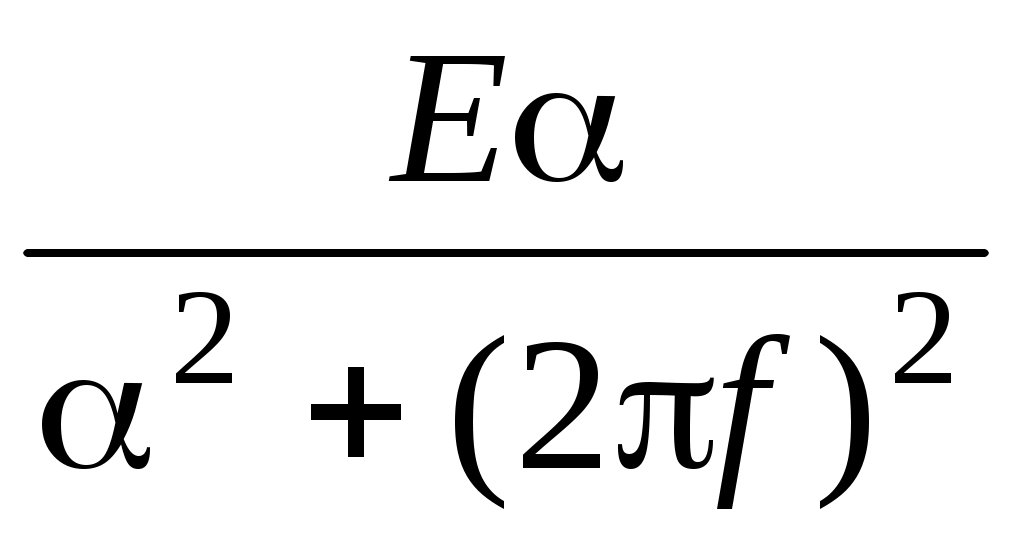– i
.
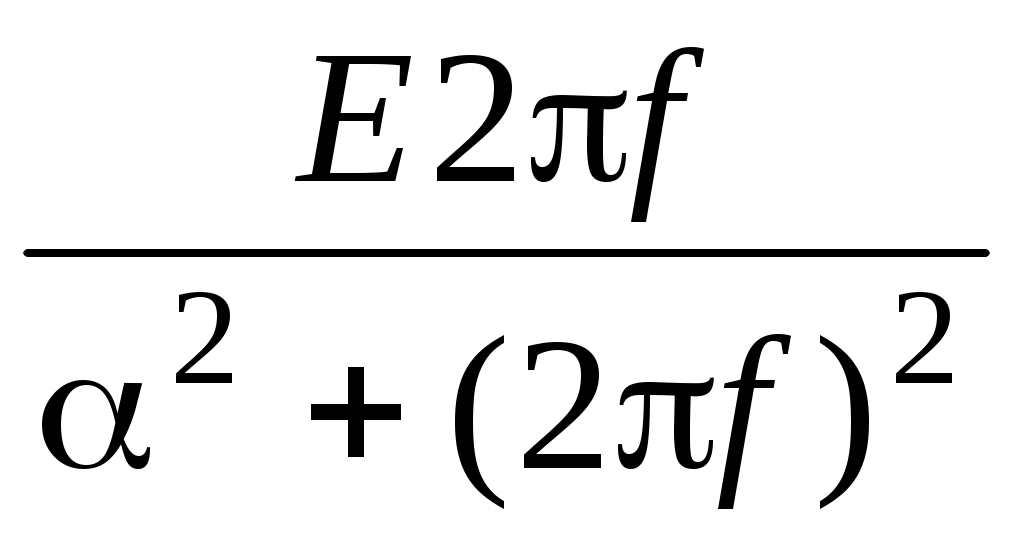Таким образом, несимметричный сигнал имеет комплексную спектральную плотность, состоящую из вещественной и мнимой частей.
Поскольку спектральная плотность комплексная, то для ее графического представления следует выделить модуль и аргумент:
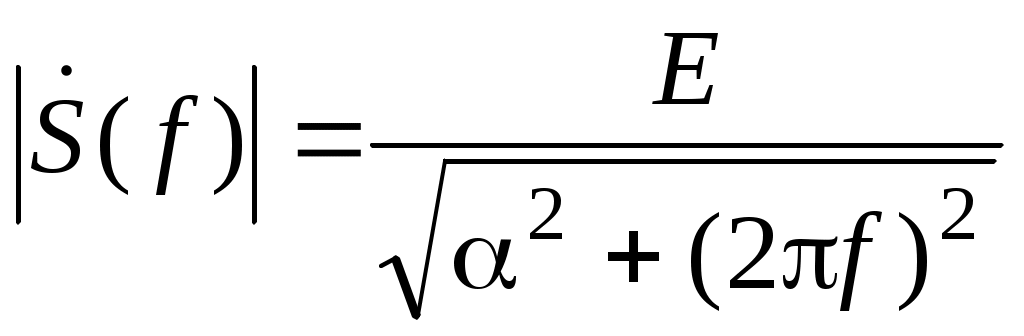= A(f) – спектр амплитуд;
arg{ } = –arctg(2f/) = (f) – спектр фаз.
Графики амплитудного и фазового спектров приведены на рис. 4.5.
Пример 4.3. Сигнал представляет собой одиночную пачку с прямоугольной огибающей длительностью tп, состоящую из трех гауссовых импульсов длительностью tи, следующих с интервалом Ти (рис. 4.6).
При построении спектральной диаграммы учтем то обстоятельство, что гауссовому сигналу вида 1exp(–1t2) в частотной области соответствует тоже гауссова функция, но отличающаяся масштабом: 2exp(–2 f2).
Второе эмпирическое правило, помогающее получить спектр данного сигнала, состоит в том, что при переходе от времени к частоте огибающей исходного сигнала будет соответствовать заполнение спектральной диаграммы, а заполнению сигнала – огибающая спектра.
Огибающая сигнала – прямоугольная функция длительностью tп. Ее спектральная плотность была получена в примере 4.1 – это функция sinc. Поскольку интервал tп велик, то согласно свойству 5, ширина функции sinc будет мала.
Заполнение – гауссовы импульсы – порождает такую же функцию в области частот. Длительность гауссовых импульсов мала, следовательно, ширина гауссовой огибающей будет большой.
Окончательно, амплитудный спектр будет выглядеть так, как показано на рис. 4.7.
Операции дискретизации и квантования уже упоминались в лекции 2. Рассмотрим их подробнее.
Упрощенная структурная схема аналого-цифрового преобразователя, осуществляющего дискретизацию и квантование, приведена на рис. 4.8.
Входной аналоговый сигнал поступает на коммутатор (К) управляемый от тактового генератора (ТГ), выборка сигнала запоминается в ячейке памяти (ЯП) и поступает на устройство сравнения (УС), сюда же подается эталонное напряжение от источника опорных напряжений (ИОН). В зависимости от результата сравнения соответствующий разряд устанавливается в логический ноль или логическую единицу. Далее цифровой код поступает в кодирующее и запоминающее устройство (КЗУ) и на выход АЦП в виде цифрового потока данных.
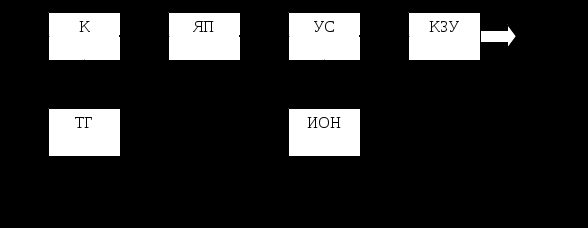
В дальнейшем цифровой поток может быть обработан в соответствии с необходимыми алгоритмами в цифровом процессоре.
Подобная схема позволяет выполнять преобразование сигналов и спектров по специально разработанным алгоритмам дискретного и быстрого преобразования Фурье (ДПФ и БПФ), а также дискретной свертки (ДС) подробнее см. в [2].
Не вдаваясь в детали, отметим, что указанные алгоритмы позволяют существенно уменьшить необходимый объем вычислений и тем самым повысить быстродействие систем обработки сигналов.
Характерной особенностью цифровых методов обработки сигналов является их дискретный характер.
Анализ дискретных сигналов и спектров базируется на фундаментальной теореме отсчетов, сформулированной в разное время независимо друг от друга Е. Уитеккером, Х. Найквистом и В.А. Котельниковым и обобщенной К. Шенноном.
Приведем формулировку теоремы, данную В.А. Котельниковым.
Пусть имеется сигнал s(t), спектр которого ограничен максимальной частотой fmax. Тогда при дискретизации этого сигнала последовательностью бесконечно коротких импульсов с интервалом
t = 1/2fmax (4.15)
потерь информации при восстановлении дискретизированного сигнала на приемной стороне не происходит.
Для иллюстрации этого рассмотрим дискретизированный сигнал и его спектр. Для упрощения спектральных преобразований в качестве огибающих сигнала (и соответственно спектра) примем гауссовы функции.
На рис. 4.9 слева показан идеальный случай дискретизации бесконечно короткими -функциями. На рис. 4.10 – реальный случай, сигнал, дискретизированный последовательностью коротких прямоугольных импульсов.
Анализируя рис. 4.9 и 4.10 можно сделать следующие выводы:
1. Спектр дискретизированного сигнала состоит из клонированных спектров исходного сигнала, он периодичен, причем период повторения по частоте равен величине, обратной интервалу дискретизации по времени.
2. В идеальном случае амплитуда клонированных спектров остается неизменной, в действительности она уменьшается с ростом частоты.
3. При точном выполнении условия теоремы Котельникова, точки смыкания первичных и вторичных спектров на частотной оси совпадают, поэтому при восстановлении сигнала с помощью идеального ФНЧ потерь информации не происходит.
4. На практике возможно перекрытие спектров и приходится нарушать т. Котельникова (4.15), вводя защитный интервал по частоте (уменьшая период следования дискретизирующих импульсов): tд =
.
5. Восстановление дискретизированного сигнала целесообразно проводить в области, близкой к нулю частот, где сосредоточена бóльшая часть его энергии.
Иногда теорему отсчетов рассматривают как интерполяционную формулу. В этом случае говорят о разложении некоторой функции по ортогональному базису функций sinc.
В области времени получим разложение вида
s(t) = s(nt) sinc[ fmax(t – nt)].
В такой интерпретации теорема отсчетов справедлива и для дискретизированных спектров:
S(f) = S(nf) sinc [ tmax(f – nf)].
Попутно заметим, что дискретному сигналу соответствует периодический спектр (см. рис. 4.9 и 4.10), а дискретному спектру будет соответствовать периодический сигнал (см. рис. 3.9, 3.10). Таким образом, при переходе от временного представления к частотному дискретизация всегда порождает периодичность.
Еще одну взаимосвязь временных и спектральных характеристик сигналов иллюстрирует теорема Винера – Хинчина:
K() =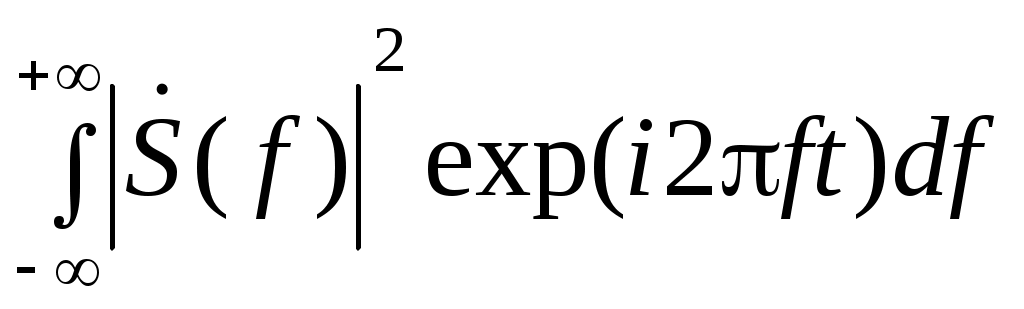
= F–1[W(f)];
W(f)=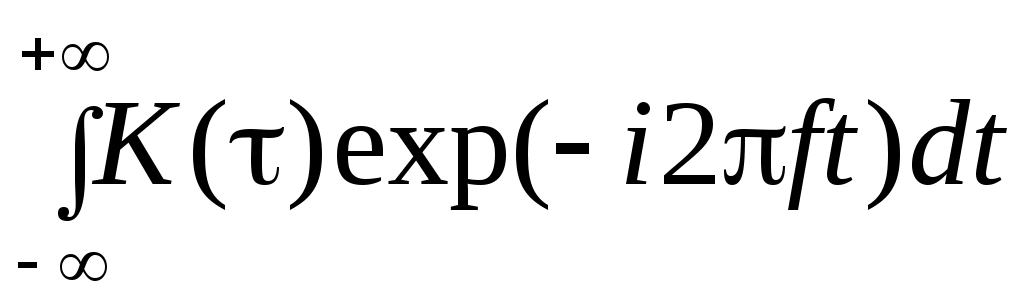
= F[K()]. (4.16)
Здесь K() – АКФ сигнала, W(f) – его энергетический спектр.
Теорема справедлива не только для детерминированных, но и для случайных сигналов.
Радиосигналы с амплитудной модуляцией. Временное и спектральное и векторное представление АМК. Энергетические характеристики АМК. Сигналы с балансной, однополосной и полярной модуляцией. Достоинства, недостатки и применение сигналов с амплитудной модуляцией.
Как уже упоминалось в лекции 2, модуляция служит для повышения эффективности передачи информации с помощью радиоволн. Амплитудно-модулированные колебания появились исторически одними из самых первых. Уже к середине 30-х годов ХХ века была предложена теория амплитудной модуляции и первые практические реализации передатчиков и приемников с АМК. В дальнейшем появились усовершенствованные способы амплитудной модуляции: балансная и однополосная АМ, а к середине ХХ века разработаны многочисленные виды модуляции для стереофонического вещания, наиболее распространенными из которых являются полярная амплитудная модуляция и модуляция с пилот-тоном.
При АМ гармоническим сигналом мгновенная частота и начальная фаза колебания неизменны, а амплитуда изменяется прямо пропорционально модулирующему сигналу:
U(t) = U0 + kАМSmcos (F0t + 0), (5.1)
где U0 – амплитуда несущей (при отсутствии модуляции) kАМ – коэффициент пропорциональности, Sm – амплитуда модулирующего сигнала, F0, 0 – мгновенная частота и начальная фаза модулирующего сигнала.
Произведение kАМSm = U представляет собой изменение амплитуды сигнала.
Величину равную M = U/ U0 называют коэффициентом амплитудной модуляции.
С учетом этого выражение (5.1) можно записать в виде
U(t) = U0 [1+ Mcos (F0t + 0)]. (5.2)
Окончательно АМК запишется в виде
uАМ(t) = U(t)cos(f0t+0) = U0 [1+ Mcos (F0t + 0)] cos(f0t+0), (5.3)
где f0, 0 – мгновенная частота и начальная фаза несущей.
Выражение (5.3) называют канонической формой записи АМК.
На рис. 5.1 проиллюстрирован процесс модуляции так называемым "чистым" тоном (гармоническим сигналом с частотой F0). Сверху изображен низкочастотный синусоидальный модулирующий сигнал U(t
Вычисление спектральной плотности осуществляем аналогично предыдущему примеру:
= = = ==
– i .Таким образом, несимметричный сигнал имеет комплексную спектральную плотность, состоящую из вещественной и мнимой частей.
Поскольку спектральная плотность комплексная, то для ее графического представления следует выделить модуль и аргумент:
= A(f) – спектр амплитуд;arg{
} = –arctg(2f/) = (f) – спектр фаз.Графики амплитудного и фазового спектров приведены на рис. 4.5.
Пример 4.3. Сигнал представляет собой одиночную пачку с прямоугольной огибающей длительностью tп, состоящую из трех гауссовых импульсов длительностью tи, следующих с интервалом Ти (рис. 4.6).
При построении спектральной диаграммы учтем то обстоятельство, что гауссовому сигналу вида 1exp(–1t2) в частотной области соответствует тоже гауссова функция, но отличающаяся масштабом: 2exp(–2 f2).
Второе эмпирическое правило, помогающее получить спектр данного сигнала, состоит в том, что при переходе от времени к частоте огибающей исходного сигнала будет соответствовать заполнение спектральной диаграммы, а заполнению сигнала – огибающая спектра.
Огибающая сигнала – прямоугольная функция длительностью tп. Ее спектральная плотность была получена в примере 4.1 – это функция sinc. Поскольку интервал tп велик, то согласно свойству 5, ширина функции sinc будет мала.
Заполнение – гауссовы импульсы – порождает такую же функцию в области частот. Длительность гауссовых импульсов мала, следовательно, ширина гауссовой огибающей будет большой.
Окончательно, амплитудный спектр будет выглядеть так, как показано на рис. 4.7.
Операции дискретизации и квантования уже упоминались в лекции 2. Рассмотрим их подробнее.
Упрощенная структурная схема аналого-цифрового преобразователя, осуществляющего дискретизацию и квантование, приведена на рис. 4.8.
Входной аналоговый сигнал поступает на коммутатор (К) управляемый от тактового генератора (ТГ), выборка сигнала запоминается в ячейке памяти (ЯП) и поступает на устройство сравнения (УС), сюда же подается эталонное напряжение от источника опорных напряжений (ИОН). В зависимости от результата сравнения соответствующий разряд устанавливается в логический ноль или логическую единицу. Далее цифровой код поступает в кодирующее и запоминающее устройство (КЗУ) и на выход АЦП в виде цифрового потока данных.
В дальнейшем цифровой поток может быть обработан в соответствии с необходимыми алгоритмами в цифровом процессоре.
Подобная схема позволяет выполнять преобразование сигналов и спектров по специально разработанным алгоритмам дискретного и быстрого преобразования Фурье (ДПФ и БПФ), а также дискретной свертки (ДС) подробнее см. в [2].
Не вдаваясь в детали, отметим, что указанные алгоритмы позволяют существенно уменьшить необходимый объем вычислений и тем самым повысить быстродействие систем обработки сигналов.
Характерной особенностью цифровых методов обработки сигналов является их дискретный характер.
Анализ дискретных сигналов и спектров базируется на фундаментальной теореме отсчетов, сформулированной в разное время независимо друг от друга Е. Уитеккером, Х. Найквистом и В.А. Котельниковым и обобщенной К. Шенноном.
Приведем формулировку теоремы, данную В.А. Котельниковым.
Пусть имеется сигнал s(t), спектр которого ограничен максимальной частотой fmax. Тогда при дискретизации этого сигнала последовательностью бесконечно коротких импульсов с интервалом
t = 1/2fmax (4.15)
потерь информации при восстановлении дискретизированного сигнала на приемной стороне не происходит.
Для иллюстрации этого рассмотрим дискретизированный сигнал и его спектр. Для упрощения спектральных преобразований в качестве огибающих сигнала (и соответственно спектра) примем гауссовы функции.
На рис. 4.9 слева показан идеальный случай дискретизации бесконечно короткими -функциями. На рис. 4.10 – реальный случай, сигнал, дискретизированный последовательностью коротких прямоугольных импульсов.
Анализируя рис. 4.9 и 4.10 можно сделать следующие выводы:
1. Спектр дискретизированного сигнала состоит из клонированных спектров исходного сигнала, он периодичен, причем период повторения по частоте равен величине, обратной интервалу дискретизации по времени.
2. В идеальном случае амплитуда клонированных спектров остается неизменной, в действительности она уменьшается с ростом частоты.
3. При точном выполнении условия теоремы Котельникова, точки смыкания первичных и вторичных спектров на частотной оси совпадают, поэтому при восстановлении сигнала с помощью идеального ФНЧ потерь информации не происходит.
4. На практике возможно перекрытие спектров и приходится нарушать т. Котельникова (4.15), вводя защитный интервал по частоте (уменьшая период следования дискретизирующих импульсов): tд =
.5. Восстановление дискретизированного сигнала целесообразно проводить в области, близкой к нулю частот, где сосредоточена бóльшая часть его энергии.
Иногда теорему отсчетов рассматривают как интерполяционную формулу. В этом случае говорят о разложении некоторой функции по ортогональному базису функций sinc.
В области времени получим разложение вида
s(t) = s(nt) sinc[ fmax(t – nt)].
В такой интерпретации теорема отсчетов справедлива и для дискретизированных спектров:
S(f) = S(nf) sinc [ tmax(f – nf)].
Попутно заметим, что дискретному сигналу соответствует периодический спектр (см. рис. 4.9 и 4.10), а дискретному спектру будет соответствовать периодический сигнал (см. рис. 3.9, 3.10). Таким образом, при переходе от временного представления к частотному дискретизация всегда порождает периодичность.
Еще одну взаимосвязь временных и спектральных характеристик сигналов иллюстрирует теорема Винера – Хинчина:
K() =
= F–1[W(f)]; W(f)=
= F[K()]. (4.16)Здесь K() – АКФ сигнала, W(f) – его энергетический спектр.
Теорема справедлива не только для детерминированных, но и для случайных сигналов.
Лекция 5. Амплитудно-модулированные колебания
Радиосигналы с амплитудной модуляцией. Временное и спектральное и векторное представление АМК. Энергетические характеристики АМК. Сигналы с балансной, однополосной и полярной модуляцией. Достоинства, недостатки и применение сигналов с амплитудной модуляцией.
Как уже упоминалось в лекции 2, модуляция служит для повышения эффективности передачи информации с помощью радиоволн. Амплитудно-модулированные колебания появились исторически одними из самых первых. Уже к середине 30-х годов ХХ века была предложена теория амплитудной модуляции и первые практические реализации передатчиков и приемников с АМК. В дальнейшем появились усовершенствованные способы амплитудной модуляции: балансная и однополосная АМ, а к середине ХХ века разработаны многочисленные виды модуляции для стереофонического вещания, наиболее распространенными из которых являются полярная амплитудная модуляция и модуляция с пилот-тоном.
При АМ гармоническим сигналом мгновенная частота и начальная фаза колебания неизменны, а амплитуда изменяется прямо пропорционально модулирующему сигналу:
U(t) = U0 + kАМSmcos (F0t + 0), (5.1)
где U0 – амплитуда несущей (при отсутствии модуляции) kАМ – коэффициент пропорциональности, Sm – амплитуда модулирующего сигнала, F0, 0 – мгновенная частота и начальная фаза модулирующего сигнала.
Произведение kАМSm = U представляет собой изменение амплитуды сигнала.
Величину равную M = U/ U0 называют коэффициентом амплитудной модуляции.
С учетом этого выражение (5.1) можно записать в виде
U(t) = U0 [1+ Mcos (F0t + 0)]. (5.2)
Окончательно АМК запишется в виде
uАМ(t) = U(t)cos(f0t+0) = U0 [1+ Mcos (F0t + 0)] cos(f0t+0), (5.3)
где f0, 0 – мгновенная частота и начальная фаза несущей.
Выражение (5.3) называют канонической формой записи АМК.
На рис. 5.1 проиллюстрирован процесс модуляции так называемым "чистым" тоном (гармоническим сигналом с частотой F0). Сверху изображен низкочастотный синусоидальный модулирующий сигнал U(t