Файл: Конспект лекций СанктПетербург 2011.doc

На рис. 7.3, а изображен RC-фильтр низких частот, очевидно, что это линейная схема. При прохождении входного сигнала через такой фильтр постоянная составляющая передается без изменений, а далее с ростом частоты амплитуда гармоник уменьшается. Для определенности подадим на вход цепи синусоидальный сигнал с некоторой частотой f₀, лежащей в середине диапазона пропускания фильтра. Форма сигнала на выходе сохранится (это тоже будет гармонический процесс), изменятся только параметры: амплитуда и фаза сигнала.

Если в схему добавить полупроводниковый диод VD (рис. 7.3, б), то характер процессов существенно изменится. Предположим, что емкость С отсутствует, тогда при подаче на вход непрерывного гармонического сигнала выходной сигнал будет представлять собой прерывистую последовательность косинусоидальных импульсов, обладающую сложным спектральным составом. Добавление емкости C приведет к сглаживанию сигнала (RС-фильтр подавляет высшие частоты и на выходе получаем постоянную составляющую (которой не было в спектре входного сигнала), т.е. постоянный ток: схема работает как однополупериодный выпрямитель.


Стационарной называют такую цепь или систему, все параметры и характеристики которой остаются неизменными на интервале наблюдения, в противном случае система будет нестационарной.

В отличие от активной, пассивная цепь не содержит в своем составе источников ЭДС или тока.

Для широкополосной цепи выполняется соотношение

f/f₀ >> 1, (7.2)

где f – рабочая полоса частот, f₀ – центральная частота.

Если соотношение (7.2) не справедливо, то цепь узкополосная. Узкополосные цепи инерционны, а широкополосные – быстродействующие.

Цепь с обратной связью состоит из основного звена с коэффициентом передачи амплитуды K и фазовым сдвигом  и звена обратной связи с коэффициентом передачи амплитуды  и фазовым сдвигом  (рис. 7.4). Характер цепи с обратной связью зависит от соотношения амплитуд и фаз входного воздействия и сигнала обратной связи.

Суммарный коэффициент передачи определяется по формуле

. (7.3)

---

Точки в (7.3) над и означают комплексный характер этих величин, знак "плюс" соответствует отрицательной ОС, "минус" – положительной.

При ПОС знаменатель (7.3) может обращаться в ноль:

1 –  0.

Отсюда получаем так называемые условия баланса амплитуд и фаз:

(т.е. суммарное усиление в петле ОС равно единице),

(т.е. суммарный сдвиг фаз в петле ОС кратен 360).

При выполнении этих условий в системе возникают автоколебания (система становится генератором незатухающих колебаний).


При подаче импульсного сигнала на вход апериодической цепи отклик изменяется монотонно, для резонансной цепи сигнал на выходе имеет несколько локальных экстремумов.

Определить является ли цепь аналоговой или цифровой можно, выделив центральный обрабатывающий элемент (процессор). Если основная обработка сигнала осуществляется аналоговым процессором, то вся цепь аналоговая, если процессор цифровой, то цепь цифровая, независимо от наличия каких-либо вспомогательных (аналоговых или цифровых) цепей.

Элементы в цепях с сосредоточенными параметрами представляют собой отдельные конструктивы (конденсаторы, обладающие емкостью, резисторы, имеющие определенное сопротивление и т.п.). Цепи с распределенными параметрами (иначе их называют длинными линиями) характеризуются погонными величинами (на пример емкость на единицу длины), выделить емкость в виде отдельного элемента – конденсатора – в таких цепях нельзя.

Реакция безынерционной цепи на входное воздействие наступает мгновенно и независимо от предыдущего состояния. Цепи с последействием обладают "памятью": сигнал на выходе определяется не только мгновенным, но и предыдущими значениями входного сигнала. Как правило, сложную цепь при анализе разделяют на безынерционные нелинейные элементы и линейные (инерционные) каскады.

---

На практике часто пользуются упрощенной классификацией цепей по их назначению. Так разделяют силовые и управляющие (сигнальные) цепи, цепи постоянного и переменного тока и т.п.
Основные характеристики линейных цепей:

1. Импульсная h(t) – реакция цепи на входное воздействие в виде -функции (см. примечание к рис. 3.9).

2. Переходная g(t) – реакция цепи на входное воздействие в виде ступенчатой -функции (единичного скачка).

3. Передаточная – реакция цепи на входное воздействие в виде гармонического сигнала.

Все эти характеристики взаимосвязаны друг с другом:
h(t) = g(t);

g(t) = ; (7.4)

= F[h(t)] = .
Комплексный характер передаточной характеристики означает учет изменения не только амплитуды, но и фазы сигнала. Модуль – это амплитудно-частотная характеристика цепи (АЧХ), аргумент – фазо-частотная характеристика (ФЧХ).

Рассмотрим практически важный пример.

Пример 7.1.

Необходимо найти передаточную характеристику неискажающей цепи.

Решение.

Сигнал на выходе неискажающей цепи описывается следующим выражением:

s_вых(t) = K₀ s_вх(t – t₀),

где K₀ – постоянный масштабирующий множитель, t₀ – постоянный временной сдвиг (запаздывание сигнала).

Таким образом, сигнал на выходе представляет собой копию входного сигнала с амплитудой, измененной в K₀ раз, смещенную вправо по оси времени на величину t₀ .

Найдем спектральную плотность выходного сигнала:

= F[s_вых(t)] = F[K₀ s_вх(t – t₀)] = K₀ F[s_вх(t – t₀)].

Воспользуемся теоремой запаздывания (см. формулу (4.8)), получим:

---

= K₀ exp(–i2f t₀).

Произведение K₀ exp(–i2f t₀) здесь не что иное, как комплекснозначная передаточная функция неискажающей цепи:

= K₀ exp(–i2f t₀). (7.5)

Отсюда получим выражения для АЧХ и ФЧХ неискажающей цепи (рис. 7.5):
АЧХ = K₀ = const – равномерная во всем диапазоне частот входного сигнала;

ФЧХ = –2t₀ f – линейная во всем диапазоне частот.

Теперь можно определить импульсную характеристику неискажающей цепи:

Согласно (7.4) h_ни(t) = F^–1[ ] = F^–1[K₀ exp(–i2f t₀)]. Воспользовавшись теоремой двойственности (4.6), окончательно получим

h_ни(t) = K₀ (t–t₀). (7.6)

Существует два основных метода анализа цепей:

1. Временнóй – с использованием импульсной характеристики.

2. Частотный – с помощью передаточной характеристики.

В основе указанных методов лежит принцип суперпозиции (4.5), который можно сформулировать так: "результат суммы есть сумма результатов".
При временнóм методе сигнал в области времени разбивают на короткие интервалы, т.е. представляют в виде суммы коротких импульсов (рис. 7.6). Импульсная характеристика выступает в роли весовой функции. Сигнал на выходе цепи вычисляют с помощью интеграла Дюамеля:
s_вых(t) = 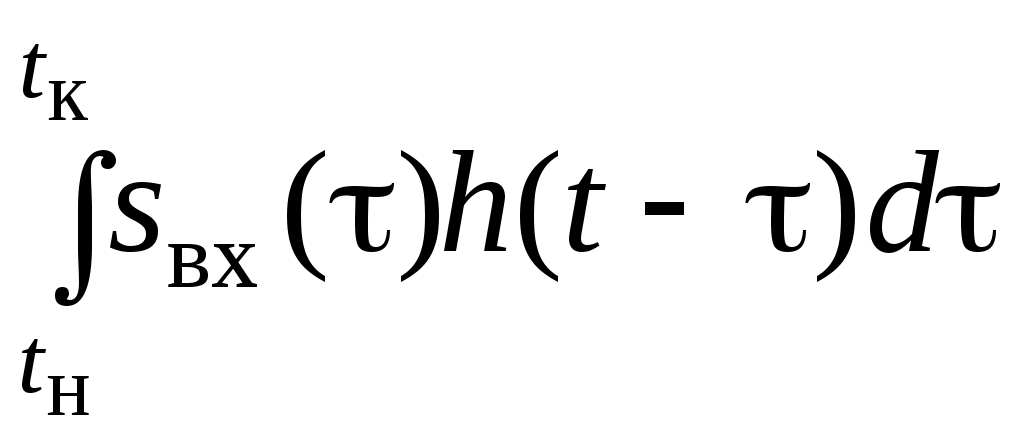. (7.7)

Сравнивая (7.7) и (2.6), можно сделать вывод, что отклик представляет собой свертку входного сигнала с импульсной характеристикой цепи:
s_вых(t) = s_вх(t) * h(t). (7.8)


Суть временного метода можно пояснить так: сложный входной сигнал представлен в виде совокупности элементарных воздействий – бесконечно коротких импульсов (-функций). Отклик цепи на каждую такую -функцию – это импульсная характеристика

---

h(t). Параметр  соответствует смещению импульсной характеристики от момента начала t_н до окончания t_к входного воздействия. Далее согласно принципу суперпозиции в результате интегрирования получаем выходной отклик цепи.

Таким образом, алгоритм временнóго метода заключается в вычислении свертки (при вычислении на компьютере используют алгоритмы дискретной свертки)
Спектральный метод расчета включает три этапа.
1. Преобразование исходного сигнала во входной спектр:

s_вх(t)  .
2. Вычисление спектра на выходе цепи:

= . (7.9)
3. Преобразование выходного спектра в сигнал на выходе.

 s_вых(t) .
Таким образом, в качестве весовой функции здесь выступает передаточная характеристика цепи.
На первом этапе по формуле, аналогичной (4.3) вычисляют Фурье-образ входного сигнала.

На втором этапе находят произведение спектральной плотности и передаточной характеристики.

Третий этап заключается в обратном преобразовании Фурье по формуле, аналогичной (4.4).

Окончательно формула для расчета выходного сигнала спектральным методом получается такой

s_вых(t) = . (7.10)

При аналитическом расчете спектральным методом часто применяют преобразование Лапласа:
s_вых(t) = , (7.11)

где р = i2f.

Взаимосвязь временнóго и спектрального метода можно проиллюстрировать так. Возьмем выражение (7.8) и выполним преобразование Фурье:

F [s_вых(t) ] = F [s_вх(t) * h(t)].

По теореме о свертке (4.13) получим

= F [s_вх(t)] F [h(t)] = ,

что эквивалентно выражению (7.9).

---