Файл: Конспект лекций СанктПетербург 2011.doc

При расчетах на компьютере используют алгоритмы дискретного и быстрого преобразования Фурье (ДПФ и БПФ).

Сравнивая вычислительную реализацию спектрального и временнóго метода, можно сделать вывод об отсутствии преимуществ одного метода перед другим. Выбор того или иного метода расчета определяется разработчиком исходя их условий конкретной практической задачи. Например, если по условию имеется спектр сигнала на входе, то целесообразнее воспользоваться спектральным методом расчета.

Рассмотрим примеры прохождения радиосигналов через линейные цепи.

Пример. 7.2. Прохождение прямоугольного импульса через идеальную и реальную дифференцирующую цепь.

Пусть на вход цепи подан одиночный прямоугольный импульс амплитудой U_m и длительностью t_и (см. рис. 2.5). Цепь осуществляет дифференцирование по времени. Определить АЧХ и ФЧХ цепи и найти сигнал на выходе.

Решение.

Сигнал на выходе идеальной дифференцирующей цепи равен
s_вых(t) = K₀ds_вх(t)/dt.

Перейдем в область частот, согласно теореме о дифференцировании (4.10) получим

= F[s_вых(t)] = i2f K₀ .

Сравнивая полученное выражение с (7.9), можно сделать вывод, что передаточная характеристика идеальной дифференцирующей цепи

= i2f K₀.

Отсюда АЧХ  = K₀ f , а ФЧХ _идц(f) = /2 (рис. 7.7).


Простейшая цепь, осуществляющая операцию дифференцирования (ФВЧ), изображена на рис. 7.8, а, а выходные сигналы, соответствующие прямоугольному импульсу, продифференцированному идеальной и реальной цепями – на рис. 7.8, б и в соответственно. Чтобы реальная цепь приближалась по свойствам к идеальной, необходимо уменьшать значение

---

RC.



Пример 7.3. Прохождение прямоугольного импульса через идеальную и реальную интегрирующую цепь.

Пусть на вход цепи подан одиночный прямоугольный импульс амплитудой U₀ и длительностью t_и (см. рис. 2.5). Цепь осуществляет интегрирование по времени. Определить АЧХ и ФЧХ цепи и найти сигнал на выходе.

Решение.

Сигнал на выходе идеальной интегрирующей цепи равен
s_вых(t) = K₀ .

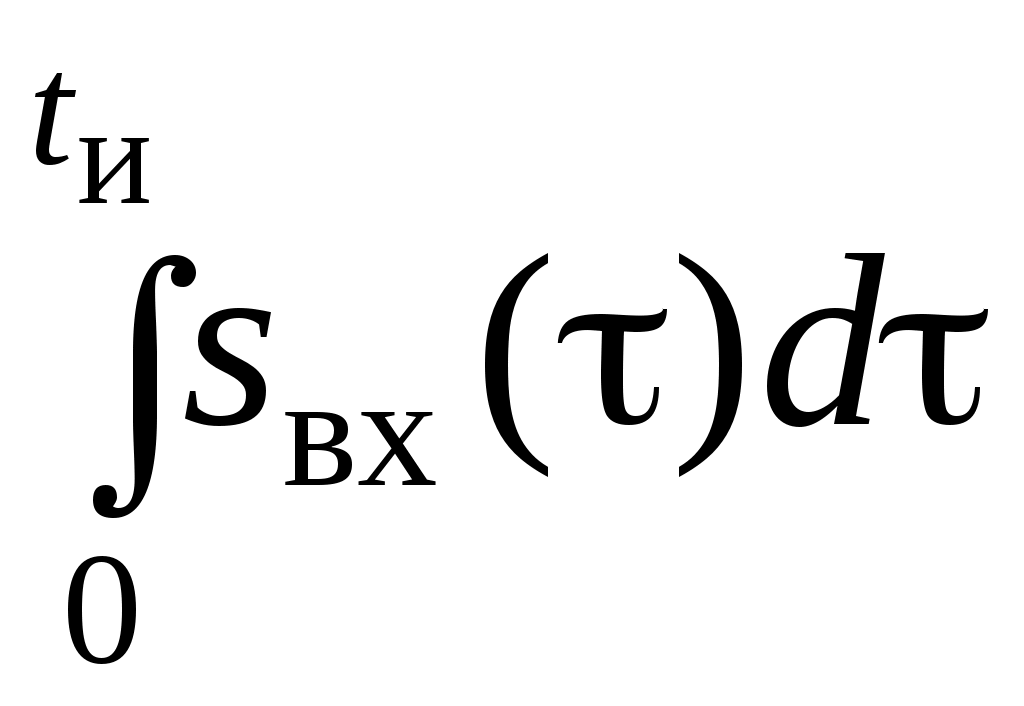Перейдем в область частот, согласно теореме об интегрировании (4.11) получим

= F[s_вых(t)] = (1/i2f) K₀ .

Сравнивая полученное выражение с (7.9), можно сделать вывод, что передаточная характеристика идеальной интегрирующей цепи

= K₀/i2f.

Отсюда АЧХ  = K₀ /f , а ФЧХ _ииц(f) = –/2 (рис. 7.9).



Простейшая цепь, осуществляющая операцию интегрирования (ФНЧ), изображена на рис. 7.10, а, а выходные сигналы, соответствующие прямоугольному импульсу, проинтегрированному идеальной и реальной цепями – на рис. 7.10, б и в соответственно. Чтобы реальная цепь приближалась по свойствам к идеальной, необходимо увеличивать значение RC.



Пример 7.4. Прохождение АМК через избирательную цепь.

Пусть на вход цепи подан амплитудно-модулированный сигнал. Амплитуда несущей равна U₀ , частота – f₀. Модуляция осуществляется чистым тоном, частота модулирующего сигнала равна F₀ (см. рис. 5.1). Положим, что начальные фазы несущей и боковых равны нулю.

АЧХ и ФЧХ избирательной цепи описывается выражениями

K(f) = , (f) = arctg (Qf/f_ц).

Найти сигнал на выходе.

---

Решение.

Поскольку по условию задачи известны АЧХ и ФЧХ цепи, воспользуемся спектральным методом.

Спектр АМК при модуляции чистым тоном был получен в лекции 5 (см. рис. 5.2).

Графики АЧХ и ФЧХ избирательной цепи приведены на рис. 7.11.

Проанализируем процесс прохождения сигнала через цепь в двух случаях:

1. При f_ц = f₀ , так называемая точная настройка.

2. При расстройке f_ц  f₀ .

Совместим спектральную диаграмму АМК и графики АЧХ и ФЧХ избирательной цепи и выполним графическое перемножение.

Полученные результаты для точной настройки иллюстрирует рис. 7.12, для расстройки – рис. 7.13.

Очевидно, что при точной настройке изменяются амплитуды несущей и боковых колебаний, кроме того боковые спектральные составляющие приобретают дополнительные равные по величине и противоположные по знаку фазовые сдвиги. В целом симметрия спектральной диаграммы выходного сигнала сохраняется.

В случае расстройки изменяются амплитуды несущей и боковых, причем эти изменения различны для спектральных составляющих ВБК и НБК. Спектральные составляющие несущей НБК и ВБК приобретают различные по величине фазовые сдвиги. В результате спектральная диаграмма выходного сигнала теряет симметрию, следовательно, форма выходного сигнала искажается.

---

Лекция 8. Нелинейные радиотехнические цепи

Понятие безынерционного нелинейного элемента. Аппроксимация вольт-амперных характеристик нелинейных элементов. Нелинейные цепи и особенности их применения в радиоэлектронике. Основы цифровой обработки сигналов. Цифровые фильтры.
Как уже упоминалось ранее, наличие в составе цепи хотя бы одного элемента с нелинейной ВАХ делает нелинейной всю цепь. Нелинейные цепи описываются системами нелинейных дифференциальных уравнений, их решение значительно сложнее, чем линейных. Поэтому для упрощения вычислений часто используют различные виды аппроксимации нелинейных ВАХ.

Нелинейный элемент считается безынерционным, если сигнал на его выходе определяется только текущим мгновенным значением входного сигнала и не зависит от предыдущего состояния. Реальные нелинейные элементы (например, диоды или транзисторы) можно считать безынерционными, если их паразитные емкости и индуктивности пренебрежимо малы. На практике это зависит от рабочей частоты цепи. При малых частотах паразитные реактивности не сказываются на работе нелинейного элемента, но с ростом частоты их влияние становится все заметнее.

Рассмотрим основные способы аппроксимации ВАХ.

1. Кусочно-линейная аппроксимация (линеаризация).

В этом случае реальная ВАХ заменяется отрезками прямых, т.е. на каждом отдельном участке нелинейный элемент заменяют линейным, определяемым так называемым дифференциальным сопротивлением.

Простейший вариант – наличие двух участков кусочно-линейной ВАХ (рис. 8.1). До некоторого напряжения U_н ток равен нулю, а после этого линейно возрастает с некоторой крутизной S:
i(u) = 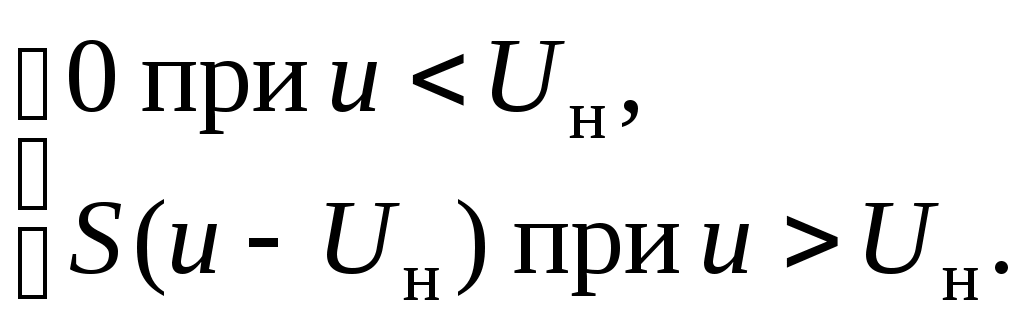(8.1)


2. Полиномиальная аппроксимация.

Кусочно-линейная аппроксимация пригодна лишь при больших амплитудах сигнала. При незначительных изменениях амплитуды используют степенную аппроксимацию в окрестности рабочей точки A при напряжении U₀ (рис. 8.2).

---

Нелинейную функцию i = f(u) в окрестности точки А можно представить в виде ряда Тейлора:
i(u) = a₀ + a₁(u – U₀) + a₂(u – U₀)² + a₃(u – U₀)³ + ... (8.2)
Коэффициенты a_n = .

Погрешность аппроксимации уменьшается с ростом числа слагаемых ряда.

Очевидно, что кусочно-линейную аппроксимацию можно рассматривать как частный случай степенной при n = 1.

3. Показательная и логарифмическая аппроксимация.

В ряде случаев используют показательную и логарифмическую функции.

Обобщенная формула для показательной аппроксимации

i(u) = i₀ u^a.

Логарифмическая аппроксимация описывается обобщенным выражением

i(u) = i₀ log_a(u).

4. Экспоненциальная аппроксимация.

Часто встречается на практике, например, ВАХ полупроводникового диода описывают выражением

i(u) = I₀[exp (u/_т) – 1],

где _т = 25 мВ – так называемый тепловой потенциал.

5. Специальные виды аппроксимации.

При необходимости применяют специальные виды аппроксимирующих функций, например многочлены Чебышева, функции Уолша и др.

Пример 8.1. Рассмотрим преобразование спектра сигнала безынерционным нелинейным элементом с кусочно-линейной ВАХ.

Пусть характеристика нелинейного элемента описывается выражением (8.1)

i(u) =

На вход подан сигнал вида

u_вх(t) = U₀ + U_mcos(f₀t+₀).

Найти спектральный состав выходного тока.

Решение.

Представим для наглядности вольт-амперную характеристику нелинейного элемента и соответствующие эпюры входного и выходного сигналов (рис. 8.3).


Из рис. 8.3 видно, что выходной сигнал представляет собой периодическую последовательность косинусоидальных импульсов длительностью t₀. период следования импульсов совпадает с периодом входного сигнала Т₀

---