Файл: Конспект лекций СанктПетербург 2011.doc

Пример 3.4. Рассмотрим практически важный случай бесконечной периодической последовательности прямоугольных импульсов с синусоидальным заполнением (рис. 3.12).


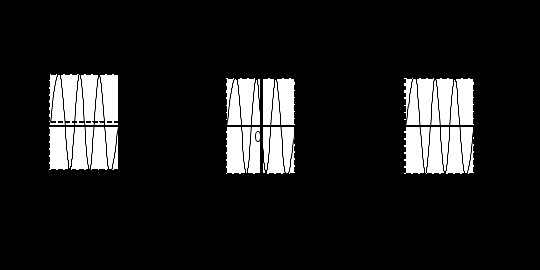
При построении спектральной диаграммы воспользуемся примерами 3.1, 3.2 и 3.3.

Из изложенного ранее можно сделать ряд выводов.

1. Поскольку последовательность бесконечная и периодическая, то спектральные составляющие будут представлять собой бесконечно короткие -функции следующие с интервалом по частоте равным 1/Т_и.

2. Так как импульсы прямоугольные, огибающая спектра является функцией sinc(ft_и).

3. Нули функции sinc(ft_и) находятся в точках с координатами кратными 1/t_и.

4. Поскольку заполнение синусоидальное и Т_и >> T₀, постоянная составляющая равна нулю.

5. И самое важное: центральная частота спектра не ноль, как во всех предыдущих примерах, а f_ц = 1/T₀, т.е. определяется частотой синусоидального заполнения (частотой несущей).

Полный амплитудный спектр приведен на рис. 3.13.


Анализируя рис. 3.13 можно понять механизм переноса спектра в ВЧ-область, реализуемый в процессе модуляции.

Исходный спектр НЧ-сигнала (см. пример 3.1) располагается в окрестности нуля частот.

Гармоническое заполнение приводит к смещению спектральных составляющих на величину f_ц, соответствующую частоте несущей. Структура спектра (амплитуды и фазы составляющих) при таком линейном переносе по частоте полностью сохраняется.

На этом основано использование ВЧ-несущей в радиосвязи: полезная информация, заложенная в структуру НЧ-сигнала (а следовательно и в структуру спектра) сохраняется, а сам сигнал является высокочастотным (его спектр располагается симметрично относительно частоты несущей f_ц) и будучи передан в антенну, порождает электромагнитные волны эффективно распространяющиеся в пространстве.

В заключение рассмотрим еще один пример, иллюстрирующий важное свойство спектров, – их суперпозицию.

Пример 3.5. Пусть сигнал представляет собой последовательность импульсов сложной формы (рис. 3.14). Требуется построить его спектральную диаграмму.

Для решения задачи сначала представим исходный сигнал в виде суммы двух вспомогательных сигналов (рис. 3.15):

---

s_п(t) = s₁(t) + s₂(t).
Поскольку вспомогательные сигналы представляют собой последовательности прямоугольных импульсов, то их спектральные диаграммы легко получить по аналогии с примером 3.1, учитывая, изменение амплитуды и длительности.

Теперь по принципу суперпозиции получим результирующую спектральную диаграмму (рис. 3.16) как сумму спектров вспомогательных сигналов.
Примечание. Для упрощения приведен только спектр амплитуд, изменение фазовых соотношений из-за смещения импульсов не учитываем.


Рис. 3.15


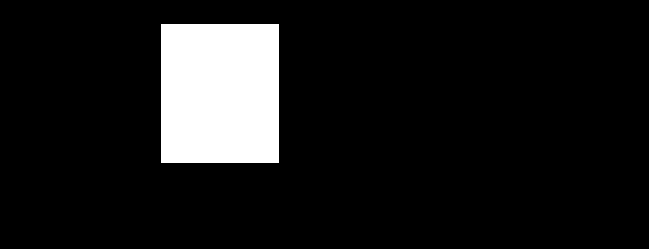
Р ис. 3.16
На рис. 3.16 огибающая спектра сигнала s₁ показана штрихпунктирной линией, огибающая спектра сигнала s₂ – пунктирной линией; спектральные составляющие (гармоники) сигнала s₂ изображены сплошной линией, гармоники сигнала s₁ – утолщенной линией.

---

Лекция 4. Дискретизация сигнала и спектра

Преобразование Фурье и его свойства. Спектральная плотность. Дискретизация и квантование. Алгоритмы ДПФ и БПФ. Теорема Котельникова. Дискретизированный сигнал и его спектр.
Пусть имеется произвольный периодический сигнал s_п(t) причем время задано в пределах от – до + (рис. 4.1).


Рассмотрим предельный переход
= s(t).

Преобразовав выражения (3.5), учитывая, что при Т_и   , nf₀  f ,    получим
A(f) = ,

B(f) = . (4.1)

Введем комплексную функцию
= A(f) –i B(f) = . (4.2)

Величина носит название спектральной плотности одиночного сигнала s(t).

Воспользовавшись теоремой Эйлера
e^–i = cos  – i sin ,

преобразуем (4.1) и (4.2) так
= = F[s(t)]. (4.3)
Непериодический сигнал при этом будет равен
s(t) = = F^–1[ ]. (4.4)

Выражения (4.3) и (4.4) носят название "прямое и обратное преобразование Фурье" (в литературе встречается также термин интеграл Фурье).

Физический смысл спектральной плотности состоит в распределении энергии сигнала вдоль частотной оси: на каких-то интервалах плотность энергии больше, а где-то меньше. Размерность модуля спектральной плотности – Вс, т.е. В/Гц.

Перечислим основные свойства преобразования Фурье.

---

1. Свойство линейности (теорема наложения, принцип суперпозиции):
F[as₁(t) + bs₂(t)] = aF[s₁(t)] + bF[s₂(t)]. (4.5)
Иными словами спектральная плотность суммы равна сумме спектральных плотностей слагаемых. С проявлением этого свойства мы уже встречались, рассматривая пример 3.5.

2. Свойство симметрии (теорема двойственности, дуальность времени и частоты):

= , (4.6)
т.е. для вещественного сигнала спектральная плотность является четной функцией.

3. Теорема о центральной ординате
S(f=0) = . (4.7)

Значение ординаты спектральной плотности на нулевой частоте численно равно "площади" сигнала.

4. Свойство инвариантности к смещению (теорема запаздывания):
F[s(t–t₀)] = S(f)exp (–i2f t₀). (4.8)
Следствие: при изменении начала отсчета времени амплитудный спектр сигнала остается неизменным, изменяется только фазовый спектр.

5. Свойство неинвариантности к масштабированию (теорема об изменении масштаба):

F[s(t)] = S( ). (4.9)

При "сжатии" сигнала (>1) спектр расширяется, амплитуда составляющих уменьшается. При "растяжении" сигнала (<1) спектр сужается, амплитуда спектральных составляющих увеличивается.

6. Теорема о дифференцировании:

F[ ] = i2f . (4.10)

7. Теорема об интегрировании
F[ ] = /( i2f). (4.11)

8. Теорема о произведении:
F[s₁(t)s₂(t)] = F[as₁(t) + bs₂(t)] = F[s₁(t)] * F[s₂(t)], (4.12)
где значком "*" обозначена операция свертки функций (см. формулу (2.6)).

---

Преобразование Фурье от произведения двух сигналов равно свертке спектральных плотностей.
9. Теорема о свертке
F[s(t) * h(t)] = F[s(t)] F[h(t)]. (4.13)
Преобразование Фурье от свертки двух функций равно произведению их Фурье-образов.
10. Теорема Парсеваля
= . (4.14)
Другими словами энергия сигнала равна энергии спектра.
Перечисленные свойства позволяют существенно упростить спектральный анализ сигналов.

Рассмотрим несколько примеров.

Пример 4.1. Пусть имеется сигнал в виде одиночного импульса прямоугольной формы, причем начало отсчета времени соответствует середине импульса (рис. 4.2). Найдем его спектральную плотность.

Поставим выражение для сигнала в формулу (4.3):

= = = =

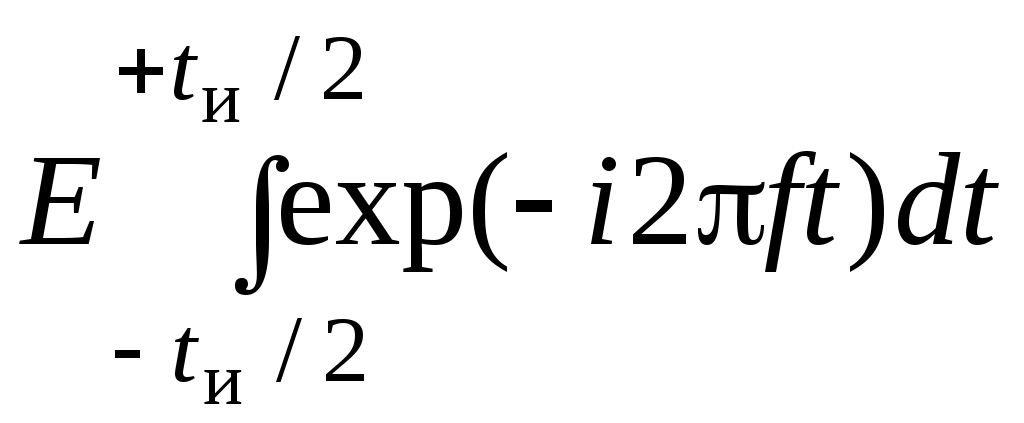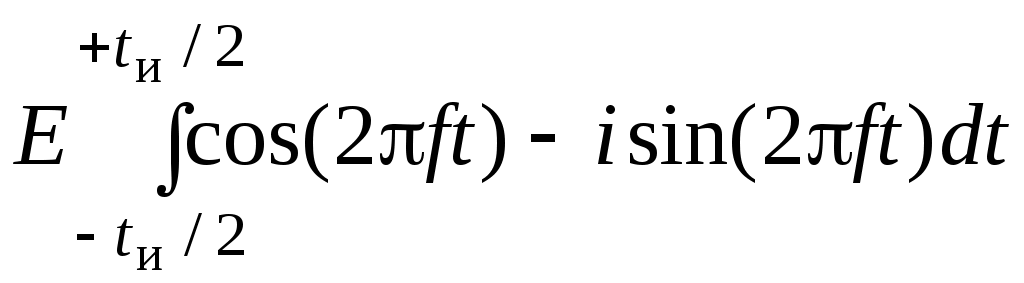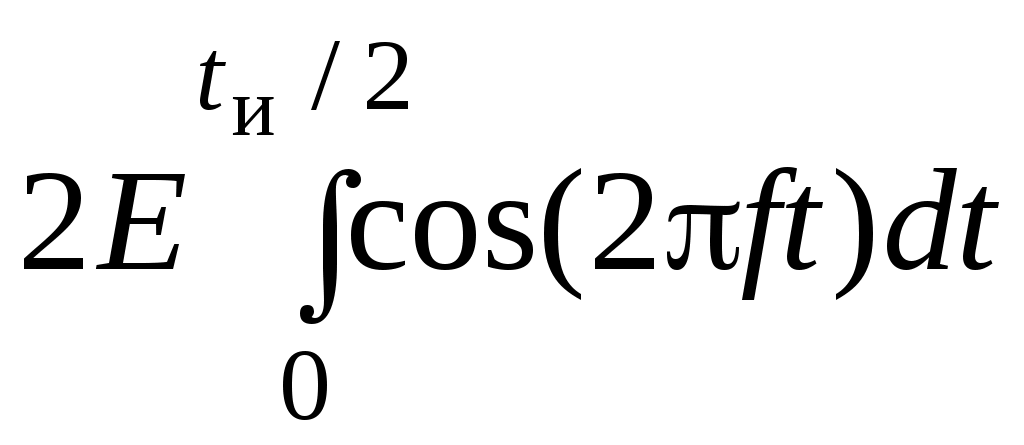= = = E/f sin (ft_и) =

= Et_и sinс (ft_и).

График спектральной плотности приведен на рис. 4.3. Как видим для четной функции получился чисто вещественный спектр, что соответствует свойству 2.



Примечание. График спектральной плотности на рис. 4.3 симметричен относительно оси ординат (слева находится область отрицательных частот). Отрицательные частоты не имеют физического смысла, их появление – следствие комплексного характера спектральной плотности. При переходе от комплекснозначной функции к вещественной компоненты, располагающиеся в левой полуплоскости, суммируются с компонентами в правой полуплоскости.
Пример 4.2.

---