Файл: Конспект лекций СанктПетербург 2011.doc

4. Теоретически спектр бесконечен, поэтому на практике его приходится ограничивать.

5. При n > m+1 J_n(m) < 0,01, поэтому практическая ширина спектра широкополосного УМК равна 2(m+1) F₀, что существенно превышает ширину спектра узкополосного УМК и АМК (2F₀).

Общий вывод – при угловой модуляции произвольным сигналом порождается бесконечное число составляющих с частотами kf₀ lF₀, где k и l = {0, 1, 2 ...}.
Рассмотрим влияние амплитуды и частоты модулирующего сигнала на спектр ЧМК и ФМК (табл. 6.1).
Таблица 6.1
Зависимость ширины спектра ЧМ и ФМ от параметров модулирующего сигнала

ЧМК	ФМК
Несущая частота f Частота модулирующего сигнала F Амплитуда модулирующего сигнала Sm
Ширина спектра 2f = 2F(m+1) Девиация частоты fд = kчмSm Индекс m = fд/F	Ширина спектра 2f = 2F(m+1) Индекс m = kфмSm Девиация частоты fд = mF
Sm  F = const
fд  m  2f 	m  fд  2f 
Sm = const F 
fд = const m  2f  const	m = const fд  2f 

Из табл. 6.1 видно, что с увеличением динамического диапазона модулирующего сигнала ширина спектра как ЧМ, так и ФМ сигнала возрастает. Расширение частотного диапазона приводит к увеличению ширины спектра ФМ колебания.
Энергетические соотношения УМК легко получить.

Поскольку амплитуда сигнала с угловой модуляцией остается постоянной и равна U₀ , то средняя мощность тоже неизменна
Р_{ср ум} = Р₀ = U₀²/2.
Это означает, что выходные каскады радиопередатчиков с УМ могут работать в режиме "В" или "С" с наибольшим КПД. В процессе модуляции мощность перераспределяется между спектральными составляющими.

---

Отсюда преимущества УМК:
1. Хорошие энергетические характеристики.

2. Высокая помехоустойчивость.

3. Потенциально широкий частотный и динамический диапазон модулирующего сигнала.

4. Простота технической реализации.

5. Отсутствие ограничений на режимы работы выходных каскадов радиопередатчика.
Основной недостаток – большая полоса частот, занимаемая УМ-сигналом при больших индексах модуляции.

Отметим две разновидности УМК, принадлежащие к группе сложных сигналов (с большой базой): линейно-частотно-модулированный сигнал (ЛЧМ-сигнал) и сигнал с относительной фазовой манипуляцией (ОФМн-сигнал). Оба этих сигнала широко применяются в радиолокационных, телеметрических системах и системах телеуправления. Увеличение базы достигается введением сложных законов модуляции несущей: с переменной мгновенной частотой или фазой. База таких сигналов достигает значений 100 и более. Подробнее о ЛЧМ- и ФМ-сигналах см. в [2, 9].
Переходя к импульсной модуляции, рассмотрим сначала основные параметры импульсных сигналов. Пусть имеется периодическая последовательность, состоящая из импульсов s_и(t), следующих с периодом Т_п (рис. 6.8).


Основные параметры импульсной последовательности:

 амплитуда импульса U_max;

 активная длительность импульса t_и;

 время задержки t_з;

 скважность q = Т_п/ t_и;

 число импульсов на определенном временном (тактовом) интервале N.

Собственно отдельный импульс имеет дополнительные параметры: длительности фронта, вершины, спада и "хвоста" (t_ф, t_в, t_с, t_х).

Основные виды импульсной модуляции:

1. Амплитудно-импульсная модуляция (АИМ): U_max  var.

2. Фазово-импульсная модуляция (ФИМ): t_з  var.

3. Широтно-импульсная модуляция (ШИМ): q  var.

4. Кодово-импульсная модуляция (КИМ): N  var.

Рассмотрим несколько примеров.

Пример 6.2. Пусть имеется кодовая последовательность 2-4-7-5-2-2-1. Необходимо передать ее по каналу связи с использованием импульсно-модулированных сигналов.

Решение.

Представим последовательность в двоичном виде (для этого достаточно трехразрядных кодовых слов):

010 100 111 101 010 010 001

В случае АИМ каждому значению будут соответствовать некоторое значение амплитуды равное nU_max, где n – кратный множитель (рис. 6.9).

---

При ФИМ временное кодовому слову соответствует определенное временное смещение импульса в пределах тактового интервала nt_з (рис. 6.10).

Простейшая реализация КИМ для BNC-кодирования была приведена на рис. 2.4.




При АИМ в простейшем случае весь динамический диапазон амплитуд делится на равные интервалы, соответствующие разрядности кодового слова (в нашем случае 7 интервалов). Амплитуда импульса на каждом тактовом интервале кратна значению кодового слова.

При простейшей реализации ФИМ амплитуда и длительность импульса остаются неизменными, а задержка относительно начала тактового интервала кратна значению кодового слова.

Для КИМ характерна взаимосвязь между числом импульсов на тактовом интервале и значением кодового слова.

Помимо рассмотренных простейших реализаций создано множество более сложных для специальных применений.

В табл. 6.2 приведено сравнение параметров различных видов импульсной модуляции при условии, что уровни исходного модулирующего сигнала равновероятны. Видно, что наилучшими свойствами обладает КИМ.
Таблица 6.2

Сравнение простейших сигналов с импульсной модуляцией

Параметр сигнала	Вид модуляции
	АИМ	ФИМ	КИМ
Ширина спектра	1/3Тт	8/3Тт	1/Тт
Средняя мощность	0,36U 2max	0,125U 2max	0,5U 2max

1>

---

Преимущества сигналов с импульсной модуляцией:

1. Высокая помехоустойчивость и точность передачи информации.

2. Возможность использования различных кодов, в том числе корректирующих и исправляющих ошибки.

3. Возможность шифрования передаваемых сообщений.

4. Возможность временного и частотного уплотнения каналов связи.

Среди недостатков следует отметить сложность аппаратуры синхронизации, кодирования и декодирования.

Одним из частных случаев является тональная КИМ, при которой лог. 0" кодируется одной частотой, а лог. "1" – другой. Подобные разновидности импульсной модуляции используются, например, в системах радиолюбительского телетайпа (RTTY), при факсимильной телетайпной и др. видах связи.
В настоящее время получают все большее распространение такие сложные виды модуляции, как OFDM (Orthogonal Frequency Divide Multiplexing), QAM (Quadrature Amplitude Modulation) и QPSK (Quadrature Phase Shift Key) и др.

Некоторые области применения модулированных сигналов приведены в табл. 6.3.
Таблица 6.3
Области применения модулированных сигналов

Область применения	Вид модуляции
	Нет	АМ	БАМ	ОБП	УМ m<1	УМ m>1	ЛЧМ	ФМн	ИМ	QAM	QPSK
Радиосвязь телеграфом	+	+
Телефонная радиосвязь		+	+	+
Профессиональная связь			+	+	+
Любительская радиосвязь	+			+	+
Радиовещание		+				+
Передача сигнала изображения в аналоговом ТВ				+
Передача сигнала звука в аналоговом ТВ						+
Передача сигнала цветности в аналоговом ТВ						+				+
Цифровое радио- и ТВ-вещание								+	+		+
Радиолокация					+		+	+	+
Радионавигация	+							+
Телексная, факсимильная и т.п. связь								+	+		+
Компьютерные сети								+	+		+
Телеметрия и телеуправление								+	+		+

---

Примечание. Знак "+" означает возможность применения данного сигнала

Лекция 7. Линейные радиотехнические цепи

Классификация радиотехнических цепей. Параметры и характеристики линейных цепей. Методы анализа линейных цепей. Прохождение радиосигналов через линейные цепи.
Классификация радиотехнических цепей (систем) приведена на рис. 7.1.



Любая цепь как система описывается совокупностью дифференциальных уравнений n-го порядка. Максимальный порядок дифференциальных уравнений, описывающих радиотехническую цепь, определяется числом независимых реактивных элементов (емкостей и индуктивностей). Так цепь на рис. 7.2, а первого порядка, а на рис. 7.2, б – второго.


Число полюсов определяется количеством независимых контуров цепи. Как правило, рассматривают многополюсники с четным числом полюсов. Самые распространенные из них – четырехполюсники, имеющие один вход и один выход (рис. 7.2). Для теоретического описания четырехполюсников разработаны системы Y-, Z-, H- и G-параметров. Пример – описание транзистора как четырехполюсника системой H-параметров:
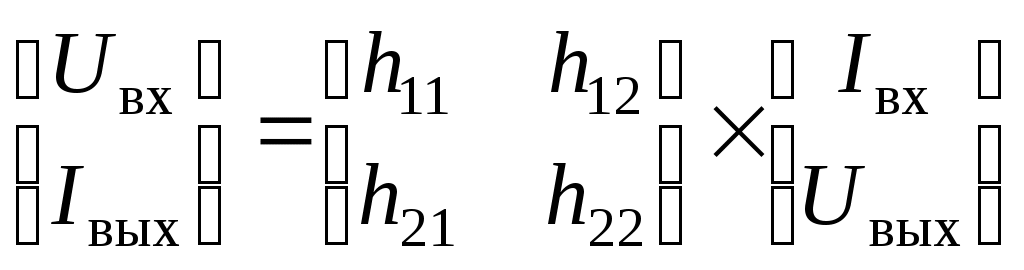. (7.1)
Здесь h₁₁ – входное сопротивление, h₁₂ – коэффициент обратной связи по напряжению, h₂₁ – коэффициент передачи по току, h₂₂ – выходная проводимость.

Подразделение цепей (систем) на линейные и нелинейные – одно из фундаментальных.

В теории систем рассматривают две основные задачи: анализ и синтез.

С точки зрения анализа цепь считают линейной, если она состоит только из линейных элементов (сопротивлений, емкостей, индуктивностей без сердечника, источников напряжения и тока). Для таких элементов выполняется закон Ома: линейная связь между падением напряжения на элементе и током через него. Добавление хотя бы одного нелинейного элемента (например, вентильного диода) превращает всю цепь в нелинейную.

С точки зрения синтеза ставят вопрос о назначении цепи. Некоторые задачи хорошо выполняют линейные цепи, а в других случаях без нелинейных элементов не обойтись. В самом общем случае можно считать, что линейные цепи выполняют фильтрацию сигнала, т.е. пропускание одних спектральных составляющих и подавление других. В процессе фильтрации происходит обеднение спектра сигнала. Нелинейные цепи способны порождать новые спектральные составляющие, которые отсутствовали в спектре исходного сигнала. Различия между линей ной и нелинейной цепью иллюстрирует рис. 7.3.

---