Файл: Курсовая работа по дисциплине моделирование систем и процессов на тему Построение математической модели абсорбера.docx
Добавлен: 25.10.2023
Просмотров: 107
Скачиваний: 7
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Таблица 2.6 – Результаты вычислений статической характеристики
| Хар-ки | №1 | №2 | №3 |
| ymax | 335755 | 112256 | 79746 |
| ymin | 146013 | 53724 | 40239 |
| yср | 244604,5833 | 89668,54545 | 62583,2 |
| S2 | 4176365576 | 480067482,9 | 240087216,6 |
| σ | 64624,8062 | 21910,44232 | 15494,74803 |
2.2 Проверка результатов измерений по критерию грубой ошибки
Для оценки выборочных данных по критерию наличия грубой ошибки (R критерий) для каждой выборки, полученной в результате проведения параллельных опытов, вычисляются величины:
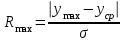 и
и 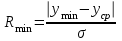 .
.Таблица 2.7 – Расчетные значения Rmax,Rmin,Rкр
| | №1 (12) | №2 (11) | №3 (10) |
| Rmax | 1,410455551 | 1,030899067 | 1,107652733 |
| Rmin | 1,525599675 | 1,640521215 | 1,44204991 |
| Rкр | 1,8 | 1,81 | 1,83 |
Расчетные значение Rmax и Rmin сравниваются с Rкр.Приведены в таблице 2.7 Табличное значение Rкр выбирают для уровня значимости α и числа степеней свободы
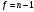 , где
, где 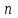 - объем выборки.. Если
- объем выборки.. Если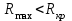 (или
(или 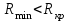 )
)принимают, что отклонение
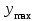 (или
(или 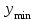
) определяется случайными явлениями и принадлежит данной генеральной совокупности, в противном случае результат отбрасывается как грубый промах и оценку по R-критерию повторяют для следующего
 (или
(или  ) с пересчитанными значениями основных статистических характеристик.
) с пересчитанными значениями основных статистических характеристик.| Rmax< Rкр | Rmin< Rкр |
| 1,410455551<1,8 | 1,525599675<1,8 |
| 1,030899067<1,81 | 1,640521215<1,81 |
| 1,107652733<1,83 | 1,44204991<1,83 |
2.3 Определение дисперсии воспроизводимости по критерию Бартлета
Дисперсию воспроизводимости (
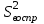 ) определяют путём сравнения выборочных дисперсий для параллельных опытов. При одинаковом числе опытов во всех выборках для сравнения дисперсий пользуются критерием Кохрена, а при различном числе - критерием Бартлета.
) определяют путём сравнения выборочных дисперсий для параллельных опытов. При одинаковом числе опытов во всех выборках для сравнения дисперсий пользуются критерием Кохрена, а при различном числе - критерием Бартлета.Рассчитывается средневзвешанное значение дисперсии:
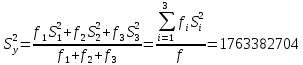
и величины
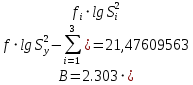
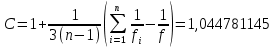
где n - число сравниваемых дисперсий.
Если выполняется равенство
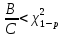
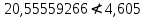
где
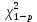 - табличное значение для
- табличное значение для 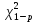 с
с 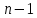 степенями свободы.
степенями свободы. Если при сравнении дисперсий по критерию Кохрена или по критерию Бартлета принято решение о значимом различии между дисперсиями, то в качестве дисперсии воспроизводимости выбирают наименьшую из сравниваемых дисперсий.
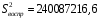
Значение
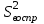 , определённое на этом этапе, в последующем используется для оценки адекватности построенной математической модели.
, определённое на этом этапе, в последующем используется для оценки адекватности построенной математической модели.
-
Построение математической модели
-
Определение порядка и расчет коэффициентов модели
-
Построение графика зависимости между выходной переменной моделируемого процесса и входными переменными по экспериментальным данным.
Исходя из таблицы 2.4 активных экспериментов, берем переменные значения и составляем таблицу 3.1 для построения графика:
Таблица 3.1 – Результаты экспериментов переменных значений
| | 5 | 10 | 15 | 20 | 25 | 30 |
| 30 | 25956 | 16625 | 17446 | 31729 | 31581 | 22028 |
| 40 | 18930 | 24979 | 21621 | 14700 | 16933 | 31344 |
| 50 | 29387 | 29196 | 23612 | 16145 | 24276 | 19590 |
| 60 | 17479 | 27566 | 22178 | 29585 | 26377 | 25416 |
| 70 | 15313 | 24661 | 22435 | 20309 | 20409 | 29804 |
В результате у нас получился график (приложение А) описывающий зависимость выходной переменной моделируемого процесса от двух входных переменных.
Процесс создания модели начинается с выбора типа модели и, как правило, на первом этапе останавливаются на линейном варианте в форме алгебраического многочлена:
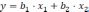 | |
где,
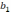
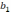 ,
, 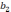
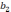 - неизвестные коэффициенты модели,
- неизвестные коэффициенты модели,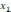
 ,
, 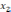
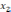 - варьируемые входные параметры объекта.
- варьируемые входные параметры объекта.Поиск неизвестных коэффициентов осуществляют с помощью регрессии по методу наименьших квадратов. При выполнении курсовой работы для расчета коэффициентов модели используем пакет прикладной программы - Microsoft Excel [5].
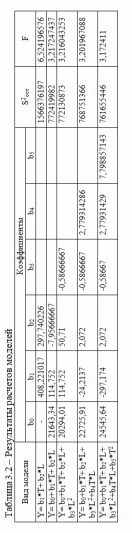
Результаты расчетов неизвестных коэффициентов приведены в таблице 3.2
-
Проверка модели на адекватность
Значения коэффициентов в уравнении регрессии, полученные по методу наименьших квадратов, являются оптимальными для выбранной математической модели, однако не всегда корректно останавливаться на этом. Процесс создания модели должен заканчиваться объективной оценкой, насколько точно построенная модель описывает идентифицируемый объект.
Проверка модели на адекватность производится путём сравнения суммы квадратов отклонений экспериментальных данных от рассчитанных по модели (остаточная дисперсия
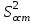 ) с показателем точности проводимых измерений (дисперсия воспроизводимости
) с показателем точности проводимых измерений (дисперсия воспроизводимости  ). Подобная процедура известна в теории регрессионного анализа под названием "критерий Фишера" (F -критерий). С помощью этого критерия производят сравнение двух дисперсий, рассчитывая отношение большей дисперсии к меньшей и сравнивая полученный результат с табличным значением.
). Подобная процедура известна в теории регрессионного анализа под названием "критерий Фишера" (F -критерий). С помощью этого критерия производят сравнение двух дисперсий, рассчитывая отношение большей дисперсии к меньшей и сравнивая полученный результат с табличным значением. 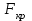 , выбранным для уровня значимости
, выбранным для уровня значимости 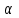 и чисел степеней свободы
и чисел степеней свободы 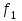 и
и 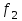 для
для 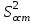 и
и  соответственно (
соответственно (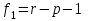 ,
,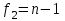 ).
).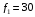
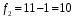
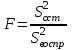
,
Если
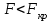 ., то с достоверностью в (1 - )*100% считают модель адекватной объекту, если нет - с той же достоверностью вероятно противоположное утверждение.
., то с достоверностью в (1 - )*100% считают модель адекватной объекту, если нет - с той же достоверностью вероятно противоположное утверждение. | F |
| 6,524196576>2,16 |
| 3,217247437>2,16 |
| 3,216043253>2,16 |
| 3,201967088>2,16 |
| 3,172411>2,16 |
В данном случае адекватную модель по критерию Фишера найти не удалось, но из всех рассчитанных наиболее подходящая модель является
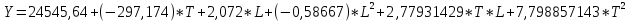
На рисунке 2 (приложение А) показан график зависимости входных переменных построенный по модели.
Заключение
В ходе работы был изучен абсорбционный метод осушки газа. Были найдены и обработаны результаты активного эксперимента расхода осушенного газа при изменении его температуры и расхода абсорбента, состоящего из 30 опытов.
Было проведено 3 параллельных эксперимента и определены статические характеристики: максимальное, минимальное и среднее значения, а так же дисперсия и среднеквадратичное отклонение.
На основании полученных данных для каждого опыта была проведена проверка по критерию грубой ошибки.
На основе полученных данных строится математическая модель абсорбера. Неизвестные коэффициенты находятся с помощью регрессии по методу наименьших квадратов на основе данных активного эксперимента. Затем была рассчитана остаточная дисперсия.
Для данной модели была проведена проверка на адекватность по критерию Фишера. Она проводилась путем сравнения рассчитанного значения F с табличным значением и по итогу сравнения модель оказалась не адекватна.
Список использованных источников
-
Пащенко Ф.Ф. Введение в состоятельные методы моделирования систем: Учебное пособие: В 2-х частях Часть 1. Математические основы моделирования систем.- М.: Финансы и статистика, 2006.-328 стр.: ил. -
Ашихмин В.Н., Гитман М.Б., Келлер И.Э., Наймарк О.Б., Столбов В.Ю., Трусов П.В., Фрик П.Г. Введение в математическое моделирование: Учебное пособие / Под редакцией П.В. Трусова. – М.: Университетская книга, Логос,2007. – 440стр. -
Закгейм А.Ю. Введение в моделирование химико-технологических процессов .- М. Химия, 1982г.- 287с.- ил. -
Кафаров В.В. Математическое моделирование основных процессов химических производств .- М. Высшая школа, 1991г.- 400с.- ил. -
Справочник функций Excel [Электронный ресурс]. URL: http://www.scribd.com/doc/126328/-Excel. Дата обращения 20.01.2023. -
https://works.doklad.ru/view/VBpbPYIJ_ww/all.html -
https://ru.wikipedia.org/wiki/Абсорбция