Файл: Преобразование Фурье (оно нам надо для памяти) Преобразование Фурье.docx

SP-сеть - разновидность блочного шифра(симметричное шифрование), использующая совместно принципы рассеивания и перемешивания и обеспечивающая за счет этого высокую криптографическую стойкость для закрытия данных.

В простейшем варианте SP-сеть представляет собой составную «двухслойную» шифрующую структуру, используемую многократно. Итерационная шифрующая сеть объединяет S-блоки (substitution box, S-box - подстановка или замена) и P-блоки (permutation box, P-box - перестановка) в единую конструкцию.

P-блоки и S-блоки могут иметь в общем случае произвольное количество входов. P-блоки переставляют разряды двоичных чисел (изменяют веса разрядов), что обеспечивает перемешивание. S-блоки предусматривают замены значений чисел (подстановки), что дает эффект рассеивания. S-блоки могут увеличивать число единиц на выходе блока по сравнению с его входом, то есть одним из свойств S-блока является «лавинный эффект»: изменение одного бита на входе приводит к изменению многих бит на выходе. P-блоки только взаимно переставляют значения разрядов (0 и 1) внутри слова данных, не изменяя их общего количества. В SP-сети процедура шифрования со­стоит в последовательном выполнении ряда чередующихся операций перестановок и подстановок.

Продемонстрируем работу SP-сети и проявление “лавинного эффекта” в ней. Сеть состоит из двух раундов - одна перестановка(одна таблица), одна подстановка(три таблицы). На вход подается 9 бит.

Используемая таблица для подстановки:



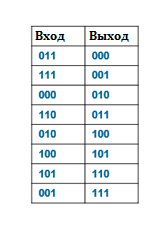
Шифруем:



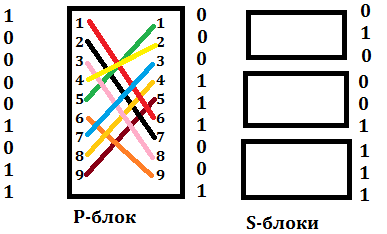
Меняем последний бит на входе и шифруем новую последовательность.



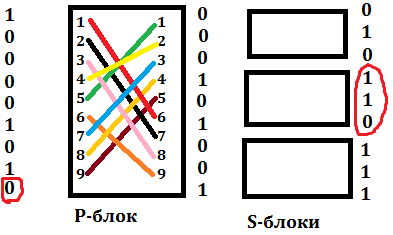
Видим, что при замене одного бита на входе на выходе поменялись три бита - проявление “лавинного эффекта” S-блока.
9. Построение таблиц прямой и обратной подстановки (для SP-сетей); требования, предъявляемые к этим таблицам. Основные правила и требования для заполнения таблиц подстановки, а также рекомендации по выбору общего числа таблиц подстановки на каждом раунде шифрования.
В простейшем случае таблица подстановки (замены) содержит две строки: в верхней строке в порядке возрастания расположены числа от 0 до N – 1, а в нижней строке – те же числа из верхнего ряда, но расставленные в другом порядке. В результате этого каждому входному числу таблицы (из верхней строки) ставится в соответствие единственный вариант замены для него (из нижней строки). Это –

---

таблица прямой подстановки, или S-блок.

Однако для расшифрования сообщения на приемном конце должна иметься парная ей таблица обратной подстановки. Таблицу обратной подстановки нетрудно получить из таблицы прямой подстановки. Для этого в таблице прямой подстановки надо упорядочить по возрастанию числа в нижней строке, при этом соответствующим образом будут переставлены и числа верхней строки. Затем верхнюю и нижнюю строки надо поменять местами.

Правила и требования для создания и заполнения таблиц подстановки:

1. 
   S-блоки предусматривают замены значений чисел (подстановки), что дает эффект рассеивания. Такой блок SP-сети должен давать максимальное рассеивание для обеспечения высокой криптостойкости. Это возможно, если в результате замены каждый выходной бит отличается от парного ему входного.
   
2. 
   Необходимо определить количество таблиц подстановки и их заполнение. Количество раундов перестановки в SP-сети будет равно количеству таких таблиц (подстановки). Здесь есть 2 варианта реализации этих таблиц(зависит от размера входного блока).
   

А) Одна таблица в одном раунде: размер входного блока равен размеру блока, подаваемого на вход SP-сети. Число возможных вариантов подстановки в этом случае равно n!, где n - число бит, подаваемых на вход SP-сети.

Б) Несколько таблиц в одном раунде: Разбить входной блок размером n бит на несколько частей - каждую из них подавать на вход своего S-блока. Тогда количество вариантов подстановки для одного S-блока равно (n/m)!, где m - количество S-блоков, n - размер блока, подаваемого на вход SP-сети.

Совокупное количество вариантов подстановки для такого раунда равно 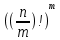, где m - количество S-блоков.

Сравним количество вариантов подстановки для случаев А и Б:

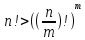- для первого случая количество вариантов подстановки больше. Значит, может быть обеспечено большее рассеяние в случае А по сравнению с Б. Чтобы при использовании нескольких таблиц в одном раунде(вариант Б) добиться такого же рассеяния, нужно включать в структуру SP-сети больше аналогичных раундов подстановки.

Конкретный пример из лекции:

Входной блок=256 бит

А) Одна таблица подстановки, подаем 256 бит: кол-во вариантов=256!

Б) Делим на части по 16 бит, 16 таблиц подстановки - общее количество вариантов подстановки для всего раунда=

---

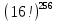
Более элементарный вычислимый пример: на вход 4 бита, случай А: кол-во вариантов=4!=24, случай Б: 2 таблицы принимают по 2 бита: 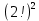= =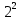4

Таким образом, использование одного S-блока в раунде подстановки обеспечивает более высокую степень рассеивания, нежели использование нескольких S-блоков меньшего размера. Для достижения безопасности на каждом раунде шифрования достаточно установить только один S-блок, но такой S-блок (в зависимости от размера шифруемого блока данных) может потребовать сравнительно большого объёма памяти. Поэтому на практике на каждом раунде часто используются S-блоки меньшего размера. Поскольку S-блок замещает блок входных бит на блок выходных бит, эта замена должна быть взаимно однозначной, чтобы гарантировать обратимость шифрующего преобразования.

В современных алгоритмах реализации SP-сетей в качестве S-блоков часто используют двоичную логическую функцию.

10. Построение блоков перестановки (для SP-сетей), их назначение, свойства и реализация.

С помощью перестановки реализуется принцип перемешивания. Блок перестановки(P-блок) изменяет лишь положение единиц и нулей в зашифрованном слове (но не их общее количество!).

P-блок (англ. permutation box or P-box) — перестановка всех бит: блок получает на вход последовательность бит, меняет местами все биты и подает результат S-блоку следующего раунда.

Важным качеством P-блока является возможность распределить вывод одного S-блока между входами как можно больших S-блоков за счет перестановки.

В SP-сети используются прямые P-блоки с n входами и n выходами. Такой блок – это перестановка с n! возможными отображениями.

Прямой P-блок обычно задают с помощью таблицы перестановок из двух строк и n столбцов. Первая строка - номера битов входящего блока, а вторая строка - номера новых битов(куда будет поставлен старый бит).

P-блок - обратимый, т.е. его можно использовать для шифрования и дешифрования. Таблицу обратной перестановки можно получить из таблицы прямой перестановки. Для этого в таблице прямой перестановки надо упорядочить по возрастанию числа в нижней строке, при этом соответствующим образом будут переставлены и числа верхней строки. Затем верхнюю и нижнюю строки надо поменять местами.

---

В современных алгоритмах реализации SP-сетей в качестве P-блоков часто используют различные математические или логические функции. Например, к P-блоку сводится циклический сдвиг, а сам P-блок фактически является частным случаем S-блока. Такие функции, как правило, легко реализуются аппаратно, обеспечивая при этом высокую скорость обработки и хорошую криптостойкость.
11. Методы анализа качества зашифрованных сообщений (на примере цифровых фотографий). Цель и смысл непосредственного визуального контроля цифрового изображения. Тест «на решетчатость»; его назначение, важнейшие свойства, реализация, примеры. Тест-гистограмма: его назначение, реализация, важнейшие свойства, примеры.
При шифровании сообщений надо правильно оценивать качество их закрытия от посторонних. Для этой цели используется ряд тестов: визуальный контроль, тест на решетчатость и тест-гистограмма. Объясним их на примере цифровых фотографий.

Визуальный контроль - самый простой метод анализа качества зашифрованных сообщений. Визуальный контроль позволяет нам определить, шумоподобно зашифрованное изображение или нет. Если на зашифрованном изображении просматриваются основные контуры исходного, значит, изображение было зашифровано неудовлетворительно. Этот простейший тест – наглядный и информативный, но все-таки он недостаточно объективен. Решение о качестве закрытия информации от посторонних принимается оператором только «на глаз», что не исключает возможность вынесения оператором ошибочных решений. Для получения объективной оценки «степени случайности» зашифрованных сообщений в дополнение к этому тесту широко применяются другие тесты(для примера с цифровой фотографией - мы вытягиваем ее в вектор числовой и анализируем уже его).

Графический тест оценки распределения чисел на плоскости - "диаграмма рассеяния", или тест "на решетчатость" предназначен для выявления зависимостей между соседними элементами в исследуемой числовой последовательности. Для этого на плоскости строится распределение чисел (элементов) последовательности B, то есть на плоскость наносятся точки с координатами (B_i; B_i+1), гдеB_i - i-й элемент последовательности B,при этом i = 0, ... , N - 1, где N - длина исследуемой последовательности

---

B. Иными словами: исследуемая последовательность B длиной N отсчетов разбивается на две последовательности X и Y (длиной N – 1 отсчетов каждая) по следующему правилу:

X = B₀, B₁, … , B_N-2; Y = B₁, B₂, … , B_N-1.

Результат теста на решетчатость - график.

Если между соседними элементами последовательности B отсутствуют функциональные зависимости, то точки на графике расположены хаотично. Если же между элементами последовательности B существуют функциональные связи, то на плоскости графика наблюдаются характерные (неслучайные) "скопления точек", образующие те или иные "линии", "фигуры" или "узоры".

А сейчас будут картинки

Пример графика результата теста "на решётчатость", выполненный для некоторой последовательности десятичных чисел, приведен ниже.



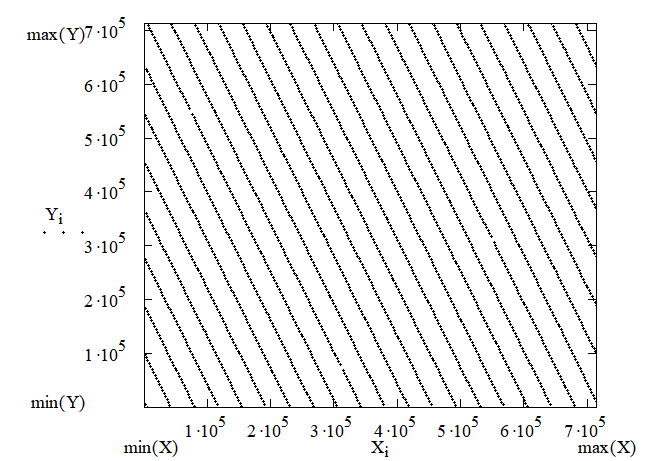
На графике видим «набор» строго периодически повторяющихся наклонных линий. Это означает, что между соседними элементами исследуемой последовательности существуют жесткие функциональные связи. Поэтому ее никак нельзя признать случайной.

Ниже приведены два примера диаграмм рассеяния для последовательностей также с заметными внутренними закономерностями. На одном из графиков просматривается характерная «решётка», а на другом видна существенная неравномерность распределения значений в виде «креста» и еще двух прямых линий.



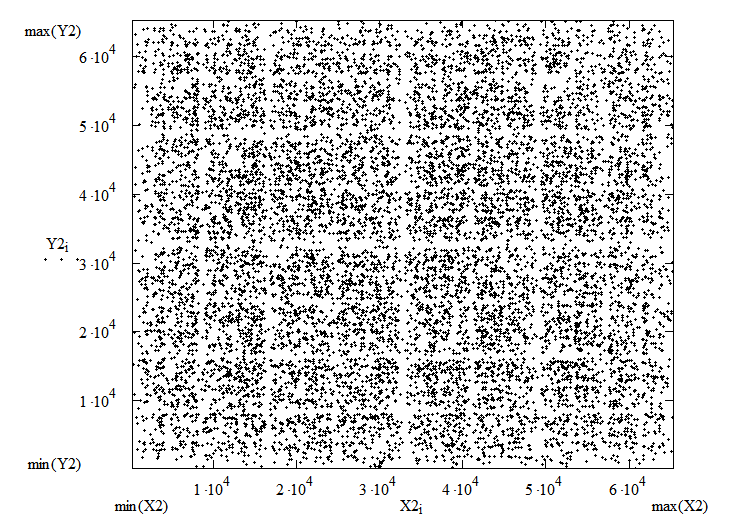
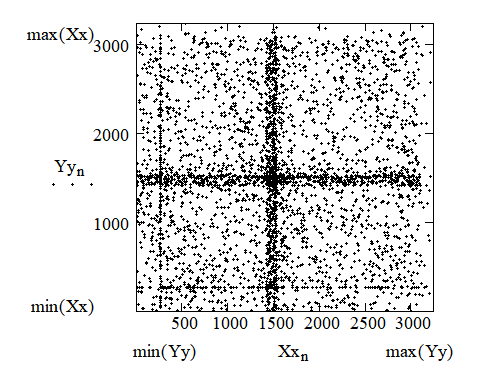
На графике теста последовательности чисел на решетчатость, представленном ниже, хорошо заметны как существенная неравномерность распределения, так и полное отсутствие в анализируемой последовательности большого ряда значений.



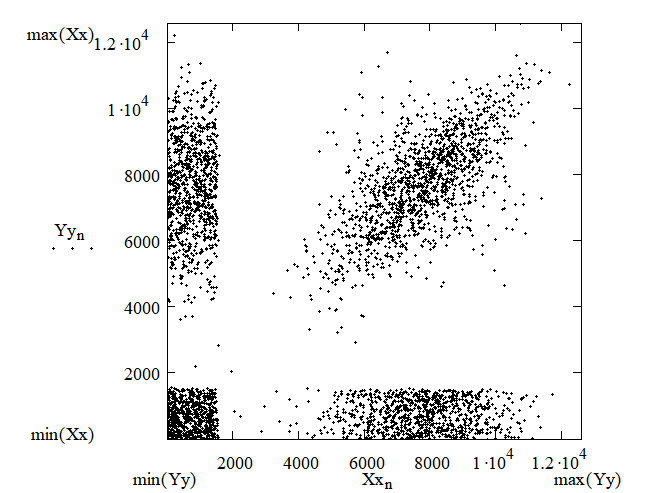
На представленном ниже графике тест на решётчатость показывает, что значения исследуемой числовой последовательности сконцентрированы относительно прямой y = x, что также свидетельствует о сильной взаимозависимости соседних отсчетов (исследуемая последовательность явно неслучайна).



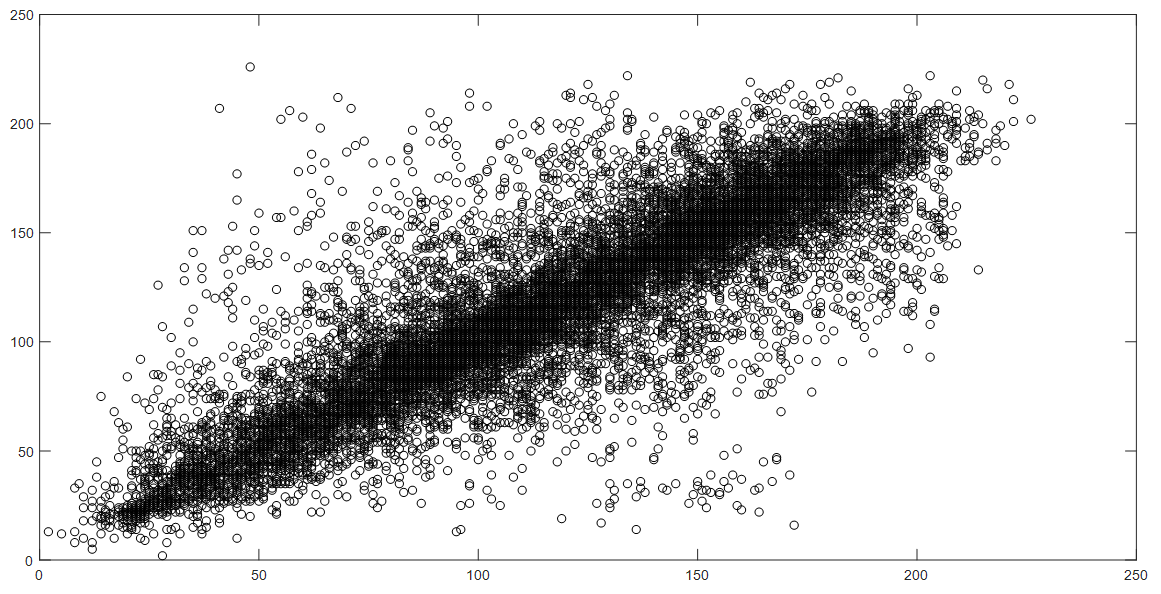
А на этом графике функциональные связи и закономерности между элементами исходной последовательности

---