ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 340
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
МОДУЛЬ 1. Предметная область метрологии
МОДУЛЬ 2. ШКАЛЫ И ПРИМЕНЕНИЕ ИХ В МЕТРОЛОГИИ
МОДУЛЬ 3. Физические величины, системы единиц физических величин
МОДУЛЬ 4. КЛАССИФИКАЦИЯ ИЗМЕРЕНИЙ. ПОНЯТИЕ О КАЧЕСТВЕ ИЗМЕРЕНИЙ
МОДУЛЬ 5. КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ
МОДУЛЬ 6. МЕТОДЫ ВЫЯВЛЕНИЯ И ИСКЛЮЧЕНИЯ ПОГРЕШНОСТЕЙ
МОДУЛЬ 7. АНАЛИЗ ТОЧЕЧНЫХ ДИАГРАММ
МОДУЛЬ 8. МАТЕМАТИЧЕСКАЯ ОБРАБОТКА И ФОРМЫ ПРЕДСТАВЛЕНИЯ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
МОДУЛЬ 13. СРЕДСТВА ИЗМЕРЕНИЙ. МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ СРЕДСТВ ИЗМЕРЕНИЙ
МОДУЛЬ 14. ЭТАЛОНЫ ЕДИНИЦ ФИЗИЧЕСКИХ ВЕЛИЧИН И ПЕРЕДАЧА ЕДИНИЦ ОТ ЭТАЛОНОВ
ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕТРОЛОГИИ
© Б.В. Цитович
МОДУЛЬ 1. Предметная область метрологии 2
МОДУЛЬ 2. ШКАЛЫ И ПРИМЕНЕНИЕ ИХ В МЕТРОЛОГИИ 12
МОДУЛЬ 3. Физические величины, системы единиц физических величин 28
МОДУЛЬ 4. КЛАССИФИКАЦИЯ ИЗМЕРЕНИЙ. ПОНЯТИЕ О КАЧЕСТВЕ ИЗМЕРЕНИЙ 45
МОДУЛЬ 5. КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ 60
МОДУЛЬ 6. МЕТОДЫ ВЫЯВЛЕНИЯ И ИСКЛЮЧЕНИЯ ПОГРЕШНОСТЕЙ 80
МОДУЛЬ 7. АНАЛИЗ ТОЧЕЧНЫХ ДИАГРАММ 89
МОДУЛЬ 8. МАТЕМАТИЧЕСКАЯ ОБРАБОТКА И ФОРМЫ ПРЕДСТАВЛЕНИЯ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ 98
МОДУЛЬ 13. СРЕДСТВА ИЗМЕРЕНИЙ. МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ СРЕДСТВ ИЗМЕРЕНИЙ 107
МОДУЛЬ 14. ЭТАЛОНЫ ЕДИНИЦ ФИЗИЧЕСКИХ ВЕЛИЧИН И ПЕРЕДАЧА ЕДИНИЦ ОТ ЭТАЛОНОВ 125
МОДУЛЬ 1. Предметная область метрологии
Метрология – наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности (РМГ 29 – 99).
Буквальная расшифровка термина метрология базируется на двух древнегреческих корнях этого слова (μέτρον – мера, размер или μέτρεω – измеряю, и λόγος – слово, учение, понятие, а также мысль, разум), и его перевод вполне соответствует термину «наука об измерениях».
В физическом плане все величины принято делить на «измеримые» и «неизмеримые». Однако, поскольку фактически измерять можно все – физические величины, уровень интеллекта, глубину художественного впечатления от некоторого зрелища, степень женской красоты и многое другое, измерения трактуют по-разному – от аппаратурной количественной оценки физических величин до приписывания чисел субъективно оцениваемым свойствам.
Неоднозначная трактовка измерений позволяет сторонникам самого широкого подхода к измерениям распространять область интересов «науки об измерениях» за пределы «чистой» метрологии. В результате метрология смешивается с квалиметрией – областью науки, занимающейся количественной оценкой качества объектов и их частных свойств.
Анализ позволяет раскрыть взаимные связи метрологии и ряда других научных и практических сфер деятельности. Такие связи можно представить в виде общих областей пересекающихся множеств. Фактические связи метрологии со стандартизацией, квалиметрией и сертификацией показаны в виде схемы на рисунке 1.1.
В каждой из представленных областей деятельности важное место занимает контроль: нормоконтроль в стандартизации, измерительный контроль в метрологии, контроль уровня качества в квалиметрии и контроль соответствия установленным требованиям в сертификации. При этом чаще всего контролируют соответствие объекта требованиям, установленным нормативными документами по стандартизации.
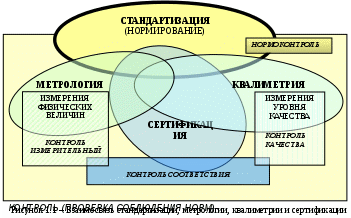
Из рисунка 1.1 следует, что при контроле соответствия в сертификации применяют
как экспертные методы, так и заимствованные у метрологии аппаратурные средства. Измерительный контроль (контроль с использованием средств измерений) и органолептический контроль (контроль с использованием органов чувств эксперта) более подробно рассмотрены в приложении А к настоящему модулю.
Наиболее тесные связи метрологии со стандартизацией можно наблюдать в следующих областях:
-
установление единиц физических величин и их воспроизведения техническими средствами (средствами измерений); -
передача единиц от государственного эталона ко всем рабочим средствам измерений (вплоть до наименее точных); -
получение результатов измерений и формы их представления.
Все эти вопросы являются объектами рассмотрения так называемой «законодательной метрологии» – специальной области метрологии, имеющей свою международную организацию МОЗМ (Международная организация законодательной метрологии).
Даже поверхностный анализ деятельности человека показывает, насколько важную роль играют измерения. Без измерений невозможны производство, торговля, спорт, деловые и бытовые отношения.
Измерения определенных однотипных («измеримых») свойств можно рассматривать как однозначное отображение элементов эмпирической реляционной системы {Q} на некоторую числовую реляционную систему {N} (рисунок 1.2), причем отображение {Q} на {N} должно быть изоморфным. Изоморфизм в математике – свойство одинаковости строения каких-либо совокупностей элементов, безразличное к природе этих элементов.
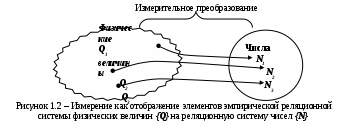
Измерительное преобразование в условиях единственности уравнения измерения и возможности существования его решения можно формально описать основным уравнением измерения:
Q = Nq,
где Q – измеряемая величина;
q – единица измеряемой величины;
N – числовое значение, определяющее соотношение между Q и q.
Следует заметить, что данное теоретическое положение идеализированно, поскольку в нем не учитываются погрешности измерений, которыми специально занимается метрология. Метрология в нашей трактовке занимается исключительно измерениями физических величин на макроуровне.
В соответствии с РМГ 29 – 99 измерение физической величины(измерение величины; измерение) – совокупность операций по применению технического средства, хранящего единицу физической величины, обеспечивающих нахождение соотношения (в явном или неявном виде) измеряемой величины с ее единицей и получение значения этой величины. В ранее действовавшем нормативном документе (ГОСТ 16263 – 70) измерение трактовали как нахождение значения физической величины опытным путем с помощью специальных технических средств.
Принципиальных отличий в приведенных определениях не наблюдается, хотя «нахождение соотношения в неявном виде» вызывает некоторые сомнения, поскольку противоречит смыслу основного уравнения измерения. Тем не менее, в РМГ 29 – 99 говорится, что приведенное в нем определение понятия «измерение» соответствует общему уравнению измерений, поскольку в нем учтена техническая сторона (совокупность операций), раскрыта метрологическая суть измерений (сравнение с единицей) и показан гносеологический аспект (получение значения величины).
От термина «измерение» происходит термин «измерять», наряду с которым нередко применяются такие термины, как «мерить», «обмерять», «замерять», «промерять», а также «обмер», «замеры» и ряд других. Это нестандартные термины и применять их не следует.
Физическая величина (величина; ФВ) – одно из свойств физического объекта (физической системы, явления или процесса), общее в качественном отношении для многих физических объектов, но в количественном отношении индивидуальное для каждого из них.
Определение не отвечает требованиям конкретности и однозначности, например, ему соответствует число конфет в коробке или бутылок минеральной воды в ящике. Приведенные примеры относятся скорее к «счетным величинам», чем к физическим. Можно подобрать и другие примеры, однако, мы относим к физическим величинам те, которые признаны таковыми. Причем наряду с величинами, безусловно относящимися к физическим (масса, длина, температура, сила электрического тока и др.), в системах единиц физических величин присутствуют частота, разрешающая способность оптических систем, и даже единица количества вещества – полные аналоги числа штучных товаров в одной упаковке (такие величины выше определены как «счетные»). Одним из определяющих признаков физической величины является возможность аппаратурного (инструментального) измерения, для чего средством измерения воспроизводится единица измеряемой физической величины.
Для измерения интересующего нас свойства (физической величины) средство измерения приводят во взаимодействие с объектом, который является носителем соответствующего свойства. Как правило любой объект измерения характеризуется некоторым множеством физических величин (ФВ1,..., ФВn, или Q1,..., Qn). Например, любой предмет имеет массу (она реализуется на предмете как одна физическая величина), размеры (реализуются как множество физических величин номинально разных и номинально одинаковых), плотность, твердость, электрические и магнитные характеристики. Физическая величина, присущая конкретному объекту, является не единственной его характеристикой. Поэтому измерение некоторой заданной физической величины можно представить моделью, показанной на рисунке 1.3. Очевидно также, что результат измерения Хi не может идеально отражать измеряемое свойство и отличается от истинного значения измеряемой физической величины Qi. Отсюда естественно возникает разговор о точности измерений.
Точность результата измерений (точность измерений) – одна из характеристик качества измерения, отражающая близость к нулю погрешности результата измерения. Поскольку точность измерения тем выше, чем меньше его погрешность, для количественной характеристики точности измерений обычно используют значения погрешностей.
Погрешность результата измерения (погрешность измерения) – отклонение результата измерения от истинного (действительного) значения измеряемой величины.

Упоминание в определении действительного значения измеряемой величины некорректно, поскольку само оно не совпадает с истинным значением измеряемой величины, и, следовательно, не может быть базой для отсчета погрешности. Погрешность измерения можно представить в виде разности между результатом измерения (полученным при измерении значением физической величины) и истинным значением физической величины
∆ = х – Q,
где ∆ – погрешность измерения,
х – результат измерения (полученное при измерении значение физической величины),
Q – истинное значение физической величины.
Необходимость измерений в любом промышленном производстве проиллюстрирована рисунком 1.4.
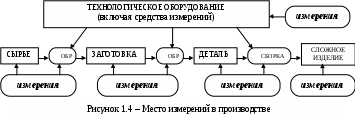
Измерения необходимы для оценки любого объекта трансформации (сырья, заготовки, детали, сборочной единицы) до ее начала, во время ее проведения и по окончании. В любом технологическом процессе надо знать, с чем приходится работать, чтобы планировать сам процесс, следить за тем как процесс идет, чтобы при необходимости корректировать его. Результат переработки исходного объекта тоже подлежит измерениям для оценки его качества и принятия управляющих решений (пропустить далее в обработку, продажу, эксплуатацию, забраковать, вернуть на переработку, корректировать техпроцесс...).
Определяющее значение измерения имеют и для любых экспериментальных исследований. Д.И.Менделеев сказал: «Наука начинается там, где начинают измерять. Точная наука немыслима без меры». Галилео Галилею приписывают слова: «Измерять то, что измеримо, делать измеримым то, что пока что неизмеримо». Место измерений в экспериментальных научных исследованиях, проводимых с использованием не только визуальных, но и аппаратурных средств фиксации результатов, показано на рисунке 1.5.
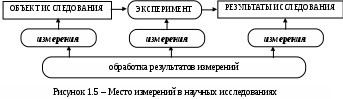
Достоверные результаты исследований и выводы из них могут быть получены только при «опережающей точности измерений». Любой тонкий эффект можно зафиксировать только тогда, когда измерения позволяют выделить его из информационного шума, в том числе и обусловленного погрешностями измерений.
Обмен результатами производственной и научной деятельности, международная кооперация в науке, промышленности и торговле требуют обеспечения достоверности всех результатов производственных и научных измерений. Поэтому в метрологии вводятся такие понятия, как единство измерений и единообразие средств измерений.
Единство измерений – состояние измерений, характеризующееся тем, что их результаты выражаются в узаконенных единицах, размеры которых в установленных пределах равны размерам единиц, воспроизводимых первичными эталонами, а погрешности результатов измерений известны и с заданной вероятностью не выходят за установленные пределы.