ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 336
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
МОДУЛЬ 1. Предметная область метрологии
МОДУЛЬ 2. ШКАЛЫ И ПРИМЕНЕНИЕ ИХ В МЕТРОЛОГИИ
МОДУЛЬ 3. Физические величины, системы единиц физических величин
МОДУЛЬ 4. КЛАССИФИКАЦИЯ ИЗМЕРЕНИЙ. ПОНЯТИЕ О КАЧЕСТВЕ ИЗМЕРЕНИЙ
МОДУЛЬ 5. КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ
МОДУЛЬ 6. МЕТОДЫ ВЫЯВЛЕНИЯ И ИСКЛЮЧЕНИЯ ПОГРЕШНОСТЕЙ
МОДУЛЬ 7. АНАЛИЗ ТОЧЕЧНЫХ ДИАГРАММ
МОДУЛЬ 8. МАТЕМАТИЧЕСКАЯ ОБРАБОТКА И ФОРМЫ ПРЕДСТАВЛЕНИЯ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
МОДУЛЬ 13. СРЕДСТВА ИЗМЕРЕНИЙ. МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ СРЕДСТВ ИЗМЕРЕНИЙ
МОДУЛЬ 14. ЭТАЛОНЫ ЕДИНИЦ ФИЗИЧЕСКИХ ВЕЛИЧИН И ПЕРЕДАЧА ЕДИНИЦ ОТ ЭТАЛОНОВ
Ri.
Сравнительный анализ результатов нескольких серий измерений одной и той же физической величины позволяет оценить воспроизводимость измерений. Характеристиками воспроизводимости измерений в двух сериях могут быть значения размахов и расхождение средних значений при практическом отсутствии тенденции изменения результатов, поскольку переменные систематические погрешности обязательно приведут к низкой сходимости результатов в серии и воспроизводимости серий. В случае неравноточных МВИ можно получить также предварительную оценку систематических постоянных погрешностей для заведомо менее точной серии. Для оценки систематических постоянных погрешностей серию сравнивают с более точной «опорной» серией, если в ней не наблюдаются явные тенденции изменения результатов.
Сходимость измерений в каждой из серий и между двумя сериями можно оценить по систематическим расхождениям и отклонениям от аппроксимирующих линий (расхождениями текущих средних и размахами), причем возможную сходимость оценивают по размахам после «исправления результатов» (исключения влияния тенденции изменения результатов, если она обнаружена). О правильности измерений можно судить по значениям размахов Ri и по числовым характеристикам тенденций изменения результатов. Можно ожидать высокой правильности только в той серии, в которой размахи минимальны и тенденции изменения результатов практически отсутствуют.
Все характеристики особенно хорошо видны на точечной диаграмме с двумя сериями измерений, оформленными в одном масштабе. Примеры таких точечных диаграмм с элементами анализа приведены на рисунках 7.6 а – 7.6 з.
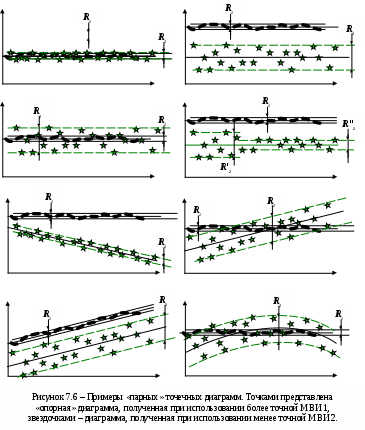
а б
в г
д е
ж з
Приведем примеры краткого сравнительного анализа двойных диаграмм, представленных на рисунке 7.6.
В тексте использованы уже встречавшиеся обозначения размахов «исправленных результатов» (R), средних значений серии наблюдений (X) и истинного значения измеряемой физической величины (Q).
Значения размахов «неисправленных результатов», средние значения каждой из серий и истинные значения измеряемой физической величины на точечных диаграммах не показаны, чтобы не загромождать рисунок. Подробный анализ каждой из диаграмм не проводится, поскольку примеры такого анализа были представлены ранее.
На диаграмме 7.6а представлены две серии без переменных систематических погрешностей (в обеих сериях отсутствуют тенденции изменения результатов), которые можно считать практически равнорассеянными, (поскольку R1 ≈ R2), но неравноточными (поскольку Х1 ≠ Х2). Неравенство средних значений свидетельствует о том, что либо одна, либо обе имеют постоянные систематические составляющие, значимые по сравнению со случайными составляющими (Х1 – Х2 > R1 ≈ R2).
Серии на диаграмме 7.6б без переменных систематических погрешностей, неравнорассеянные (поскольку R1 ≠ R2) и неравноточные (в них кроме того, что R1 ≠ R2, еще и Х1 ≠ Х2), причем либо в одной, либо в обеих сериях присутствуют постоянные систематические погрешности (если, например, считать Х1 ≈ Q, то Х2 ≠ Q, поскольку Х1 ≠ Х2).
На диаграмме 7.6в показаны серии без переменных систематических погрешностей неравноточные и неравнорассеянные (R1 ≠ R2), причем обе имеют практически одинаковые постоянные систематические составляющие (поскольку Х1 ≈ Х2).
На диаграмме 7.6г представлены две серии без переменных систематических погрешностей, неравнорассеянные (поскольку R1 ≠ R2), причем более грубая серия имеет два характерных участка с различающимися размахами (видно, что R'2 ≠ R"2). Серии неравноточные, поскольку кроме неравенства случайных погрешностей еще и Х1 ≠ Х2, следовательно различны и постоянные систематические погрешности). Одна из серий, либо обе имеют значимые постоянные систематические составляющие (поскольку Х1 ≠ Х2) .
Первая серия на диаграмме 7.6д не имеет переменных систематических погрешностей, у второй – явно выраженная тенденция изменения результатов (значения монотонно убывают, что свидетельствует о наличии прогрессирующей систематической составляющей). Серии неравноточные (
R'1 ≠ R'2), но можно графически или аналитически привести их к практически равнорассеянным (поскольку R1 ≈ R2), для чего необходимо исключить из рассмотрения переменную систематическую составляющую второй серии.
На диаграмме 7.6е представлены две серии очевидно неравноточные и неравнорассеянные. Первая серия не имеет переменных систематических погрешностей, у второй явно выраженная прогрессирующая тенденция изменения результатов (значения монотонно возрастают, что свидетельствует о наличии прогрессирующей систематической составляющей).
Две явно неравноточные и неравнорассеянные серии на диаграмме 7.6ж имеют примерно одинаковые прогрессирующие тенденции изменения результатов (однотипные возрастающие значения свидетельствуют о наличии практически одинаковых прогрессирующих систематических составляющих).
На последней диаграмме 7.6з представлены две явно неравноточные и неравнорассеянные серии, одна из которых имеет немонотонную тенденцию изменения результатов (вначале возрастающие, а затем убывающие значения свидетельствуют о наличии систематической составляющей, предположительно циклического характера). Для достоверных заключений о наличии во второй серии периодической погрешности, ее амплитуде и предполагаемом периоде наличной информации недостаточно.
В ходе решения различных измерительных задач часто встречается необходимость математической обработки результатов измерений. В литературных источниках описание математической обработки результатов измерений часто сведено к статистической обработке некоторых абстрактных данных, свободных от систематической составляющей, что фактически отражает только одну сторону проблемы.
Анализ математической обработки результатов измерений позволяет выделить следующие типовые задачи:
Третий и четвертый случаи выходят за рамки чистой метрологии, поскольку относятся к более широкому классу задач, решаемых в ходе проведения экспериментальных исследований.
В метрологии для повышения достоверности и представительности результатов достаточно часто прибегают к многократным повторениям операции измерений одной и той же физической величины. При этом каждый единичный результат называют наблюдением при измерении, а результат измерений получают как интегральную оценку всего массива наблюдений. Поэтому в метрологии под математической обработкой результатов измерений традиционно понимают обработку результатов многократных прямых или косвенных измерений одной и той же физической величины.
Математическая обработка включает два принципиально разных направления: детерминированную обработку результатов измерений и статистическую обработку. Детерминированная математическая обработка результатов измерений в обязательном порядке применяется при получении результатов косвенных измерений. Например, для определения плотности некоторого вещества измеряют массу и объем одного и того же образца, после чего рассчитывают его плотность. В линейно-угловых измерениях часто рассчитывают угол по результатам измерений длин, межосевые расстояния отверстий по координатам осей и т.д.
При наличии систематических тенденций изменения результатов многократных измерений одной и той же величины также можно применить детерминированную математическую обработку результатов. В ходе этой обработки стремятся получить аналитическое описание систематической составляющей погрешности измерений. Такое описание позволяет исключить из дальнейшего рассмотрения переменные систематические погрешности. Результаты измерений, из которых исключены систематические погрешности, в метрологии называют «исправленными». Данные после полного или частичного «исправления» можно подвергать статистической обработке. Под «частичным исправлением» мы понимаем исключение переменной систематической составляющей погрешности. В таком случае математическая обработка позволяет получить неискаженные оценки вида распределения и его моментов, кроме оценки математического ожидания (она может оказаться смещенной из-за неисключенной постоянной составляющей систематической погрешности).
Задача обработки массива результатов измерений номинально одинаковых величин может появиться в ходе измерительного контроля неидеального объекта с множеством однородных физических величин, заданных одним параметром. Если расхождения результатов в предыдущих группах задач были обусловлены только погрешностями измерений, то в рассматриваемой задаче сами измеряемые величины могут существенно различаться. Например, шарик для подшипника качения не является идеальной сферой и имеет бесконечное число толщин, которые нормированы как один диаметральный размер. Еще более сложные задачи возникают при контроле партии однородной продукции по одному из параметров, при измерениях номинально одинаковых физических величин, многократно воспроизводимых в ходе экспериментальных исследований технологических процессов и т.д.
Последняя задача – обработка результатов измерений разных величин или изменяющейся физической величины – характерна для экспериментальных исследований, связанных с выявлением характера изменения исследуемой величины (параметра) при контролируемом изменении одного или нескольких аргументов. В метрологии такие задачи характерны для поверки и калибровки средств измерений, а также для метрологической аттестации средств измерений и методик выполнения измерений.
Отсутствие четкой постановки задачи обработки результатов измерений часто приводит к недоразумениям, в том числе к искажению получаемых результатов за счет
Сравнительный анализ результатов нескольких серий измерений одной и той же физической величины позволяет оценить воспроизводимость измерений. Характеристиками воспроизводимости измерений в двух сериях могут быть значения размахов и расхождение средних значений при практическом отсутствии тенденции изменения результатов, поскольку переменные систематические погрешности обязательно приведут к низкой сходимости результатов в серии и воспроизводимости серий. В случае неравноточных МВИ можно получить также предварительную оценку систематических постоянных погрешностей для заведомо менее точной серии. Для оценки систематических постоянных погрешностей серию сравнивают с более точной «опорной» серией, если в ней не наблюдаются явные тенденции изменения результатов.
Сходимость измерений в каждой из серий и между двумя сериями можно оценить по систематическим расхождениям и отклонениям от аппроксимирующих линий (расхождениями текущих средних и размахами), причем возможную сходимость оценивают по размахам после «исправления результатов» (исключения влияния тенденции изменения результатов, если она обнаружена). О правильности измерений можно судить по значениям размахов Ri и по числовым характеристикам тенденций изменения результатов. Можно ожидать высокой правильности только в той серии, в которой размахи минимальны и тенденции изменения результатов практически отсутствуют.
Все характеристики особенно хорошо видны на точечной диаграмме с двумя сериями измерений, оформленными в одном масштабе. Примеры таких точечных диаграмм с элементами анализа приведены на рисунках 7.6 а – 7.6 з.

а б
в г
д е
ж з
Приведем примеры краткого сравнительного анализа двойных диаграмм, представленных на рисунке 7.6.
В тексте использованы уже встречавшиеся обозначения размахов «исправленных результатов» (R), средних значений серии наблюдений (X) и истинного значения измеряемой физической величины (Q).
Значения размахов «неисправленных результатов», средние значения каждой из серий и истинные значения измеряемой физической величины на точечных диаграммах не показаны, чтобы не загромождать рисунок. Подробный анализ каждой из диаграмм не проводится, поскольку примеры такого анализа были представлены ранее.
На диаграмме 7.6а представлены две серии без переменных систематических погрешностей (в обеих сериях отсутствуют тенденции изменения результатов), которые можно считать практически равнорассеянными, (поскольку R1 ≈ R2), но неравноточными (поскольку Х1 ≠ Х2). Неравенство средних значений свидетельствует о том, что либо одна, либо обе имеют постоянные систематические составляющие, значимые по сравнению со случайными составляющими (Х1 – Х2 > R1 ≈ R2).
Серии на диаграмме 7.6б без переменных систематических погрешностей, неравнорассеянные (поскольку R1 ≠ R2) и неравноточные (в них кроме того, что R1 ≠ R2, еще и Х1 ≠ Х2), причем либо в одной, либо в обеих сериях присутствуют постоянные систематические погрешности (если, например, считать Х1 ≈ Q, то Х2 ≠ Q, поскольку Х1 ≠ Х2).
На диаграмме 7.6в показаны серии без переменных систематических погрешностей неравноточные и неравнорассеянные (R1 ≠ R2), причем обе имеют практически одинаковые постоянные систематические составляющие (поскольку Х1 ≈ Х2).
На диаграмме 7.6г представлены две серии без переменных систематических погрешностей, неравнорассеянные (поскольку R1 ≠ R2), причем более грубая серия имеет два характерных участка с различающимися размахами (видно, что R'2 ≠ R"2). Серии неравноточные, поскольку кроме неравенства случайных погрешностей еще и Х1 ≠ Х2, следовательно различны и постоянные систематические погрешности). Одна из серий, либо обе имеют значимые постоянные систематические составляющие (поскольку Х1 ≠ Х2) .
Первая серия на диаграмме 7.6д не имеет переменных систематических погрешностей, у второй – явно выраженная тенденция изменения результатов (значения монотонно убывают, что свидетельствует о наличии прогрессирующей систематической составляющей). Серии неравноточные (
R'1 ≠ R'2), но можно графически или аналитически привести их к практически равнорассеянным (поскольку R1 ≈ R2), для чего необходимо исключить из рассмотрения переменную систематическую составляющую второй серии.
На диаграмме 7.6е представлены две серии очевидно неравноточные и неравнорассеянные. Первая серия не имеет переменных систематических погрешностей, у второй явно выраженная прогрессирующая тенденция изменения результатов (значения монотонно возрастают, что свидетельствует о наличии прогрессирующей систематической составляющей).
Две явно неравноточные и неравнорассеянные серии на диаграмме 7.6ж имеют примерно одинаковые прогрессирующие тенденции изменения результатов (однотипные возрастающие значения свидетельствуют о наличии практически одинаковых прогрессирующих систематических составляющих).
На последней диаграмме 7.6з представлены две явно неравноточные и неравнорассеянные серии, одна из которых имеет немонотонную тенденцию изменения результатов (вначале возрастающие, а затем убывающие значения свидетельствуют о наличии систематической составляющей, предположительно циклического характера). Для достоверных заключений о наличии во второй серии периодической погрешности, ее амплитуде и предполагаемом периоде наличной информации недостаточно.
МОДУЛЬ 8. МАТЕМАТИЧЕСКАЯ ОБРАБОТКА И ФОРМЫ ПРЕДСТАВЛЕНИЯ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
В ходе решения различных измерительных задач часто встречается необходимость математической обработки результатов измерений. В литературных источниках описание математической обработки результатов измерений часто сведено к статистической обработке некоторых абстрактных данных, свободных от систематической составляющей, что фактически отражает только одну сторону проблемы.
Анализ математической обработки результатов измерений позволяет выделить следующие типовые задачи:
-
обработка результатов прямых многократных измерений одной и той же физической величины (серии измерений); -
расчет результатов косвенных измерений физической величины, в том числе при многократных прямых измерениях каждой из величин, входящих в формулу для расчета результатов косвенных измерений; -
обработка результатов измерений массива номинально одинаковых величин; -
обработка результатов измерений разных величин или изменяющейся физической величины.
Третий и четвертый случаи выходят за рамки чистой метрологии, поскольку относятся к более широкому классу задач, решаемых в ходе проведения экспериментальных исследований.
В метрологии для повышения достоверности и представительности результатов достаточно часто прибегают к многократным повторениям операции измерений одной и той же физической величины. При этом каждый единичный результат называют наблюдением при измерении, а результат измерений получают как интегральную оценку всего массива наблюдений. Поэтому в метрологии под математической обработкой результатов измерений традиционно понимают обработку результатов многократных прямых или косвенных измерений одной и той же физической величины.
Математическая обработка включает два принципиально разных направления: детерминированную обработку результатов измерений и статистическую обработку. Детерминированная математическая обработка результатов измерений в обязательном порядке применяется при получении результатов косвенных измерений. Например, для определения плотности некоторого вещества измеряют массу и объем одного и того же образца, после чего рассчитывают его плотность. В линейно-угловых измерениях часто рассчитывают угол по результатам измерений длин, межосевые расстояния отверстий по координатам осей и т.д.
При наличии систематических тенденций изменения результатов многократных измерений одной и той же величины также можно применить детерминированную математическую обработку результатов. В ходе этой обработки стремятся получить аналитическое описание систематической составляющей погрешности измерений. Такое описание позволяет исключить из дальнейшего рассмотрения переменные систематические погрешности. Результаты измерений, из которых исключены систематические погрешности, в метрологии называют «исправленными». Данные после полного или частичного «исправления» можно подвергать статистической обработке. Под «частичным исправлением» мы понимаем исключение переменной систематической составляющей погрешности. В таком случае математическая обработка позволяет получить неискаженные оценки вида распределения и его моментов, кроме оценки математического ожидания (она может оказаться смещенной из-за неисключенной постоянной составляющей систематической погрешности).
Задача обработки массива результатов измерений номинально одинаковых величин может появиться в ходе измерительного контроля неидеального объекта с множеством однородных физических величин, заданных одним параметром. Если расхождения результатов в предыдущих группах задач были обусловлены только погрешностями измерений, то в рассматриваемой задаче сами измеряемые величины могут существенно различаться. Например, шарик для подшипника качения не является идеальной сферой и имеет бесконечное число толщин, которые нормированы как один диаметральный размер. Еще более сложные задачи возникают при контроле партии однородной продукции по одному из параметров, при измерениях номинально одинаковых физических величин, многократно воспроизводимых в ходе экспериментальных исследований технологических процессов и т.д.
Последняя задача – обработка результатов измерений разных величин или изменяющейся физической величины – характерна для экспериментальных исследований, связанных с выявлением характера изменения исследуемой величины (параметра) при контролируемом изменении одного или нескольких аргументов. В метрологии такие задачи характерны для поверки и калибровки средств измерений, а также для метрологической аттестации средств измерений и методик выполнения измерений.
Отсутствие четкой постановки задачи обработки результатов измерений часто приводит к недоразумениям, в том числе к искажению получаемых результатов за счет