Файл: Казанский национальный исследовательский технический университет им. А. Н. Туполевакаи (книтукаи).docx
Добавлен: 07.11.2023
Просмотров: 87
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
- 1 2 3 4 5 6
Построение плана ускорений
Величины нормальных ускорений звеньев определяется по формуле:
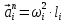
Где
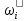 -угловая скорость движения соответствующего звена ,рад/c;
-угловая скорость движения соответствующего звена ,рад/c;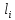 -длина соответствующего звена, м.
-длина соответствующего звена, м.Абсолютное ускорение точки A, равное его нормальному ускорению, т.к. тангенсальное равно нулю (
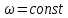 ), принадлежащей ОА, определяется по формуле:
), принадлежащей ОА, определяется по формуле: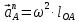 (9)
(9)где
 – угловая скорость звена ОА, рад/с;
– угловая скорость звена ОА, рад/с;  – длина звена ОА, м.
– длина звена ОА, м.Подставляя исходные данные и определим модуль ускорение точки A:
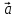 A=
A=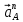 +
+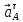 =352*0.3+0=367,5
=352*0.3+0=367,5Масштаб плана ускорений вычисляется по формуле:
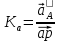
где
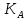 -модуль абсолютного ускорения точки А, м/
-модуль абсолютного ускорения точки А, м/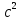 ;
; ap-отрезок на плане ускорений, мм.
Ускорению точки A, равному 480м/
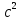 , на чертеж соответствует отрезок 240 мм. Таким образов, масштаб плана ускорений будет равен.
, на чертеж соответствует отрезок 240 мм. Таким образов, масштаб плана ускорений будет равен.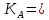 367,5/367,5=1
367,5/367,5=1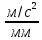
Для определения ускорения точки B используем систему векторных уравнений:
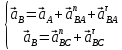
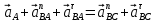 1)
1)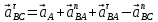
 A //AO,
A //AO, 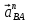 //BA,
//BA, 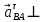 BA,
BA, 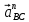 //BC,
//BC, 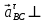 BC
BC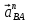 = 0.632*1.4 = 0.56 м/с2,
= 0.632*1.4 = 0.56 м/с2,  = 560.74 мм
= 560.74 мм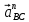 = = 17.162*0.6 = 185.8 м/с2,
= = 17.162*0.6 = 185.8 м/с2,  = 228.32 мм
= 228.32 ммгде
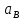 - ускорение точки B, лежащей на звене 2 и звене 3,
- ускорение точки B, лежащей на звене 2 и звене 3,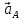 -полное ускорение точки A, его вектор отложен на плане ускорений в виде отрезка ap;
-полное ускорение точки A, его вектор отложен на плане ускорений в виде отрезка ap;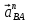 -нормальное ускорение точки B во вращательном движение звена 2 относительно A, по модулю равное
-нормальное ускорение точки B во вращательном движение звена 2 относительно A, по модулю равное 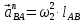 (направлено параллельно линии АВ от точки B к точке А)
(направлено параллельно линии АВ от точки B к точке А)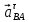 -касательное ускорение точки B во вращательном движении звена 2 относительно точки А (направлено перпендикулярно линии АВ)
-касательное ускорение точки B во вращательном движении звена 2 относительно точки А (направлено перпендикулярно линии АВ)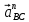 -нормально ускорение точки B во вращательном движении звена 3 относительно точки С, по модулю равно
-нормально ускорение точки B во вращательном движении звена 3 относительно точки С, по модулю равно 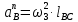 (направлено параллельно линии BC от точки B к точке С.
(направлено параллельно линии BC от точки B к точке С.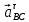 - касательное ускорение точки B во вращательном движении звена 3 относительно точки С (направлено перпендикулярно линии BC)
- касательное ускорение точки B во вращательном движении звена 3 относительно точки С (направлено перпендикулярно линии BC)Для определения ускорения точки D используем систему векторных уравнений:
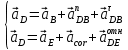 ,
,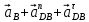 =
=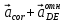
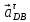 =
= 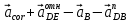
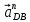
//DB,
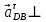 DB,
DB, 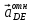 //DB
//DB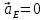
 =17.162*0.49 = 144.9м/с2,
=17.162*0.49 = 144.9м/с2, 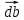 = 441.6 мм
= 441.6 мм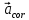 = 2VDE*
= 2VDE*  = 2*5,887*17,16=202.04 м/с2, p
= 2*5,887*17,16=202.04 м/с2, pгде
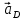 - ускорение точки D звена 4
- ускорение точки D звена 4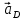 -ускорение точки D, его вектор отложен на плане ускорений в виде отрезка pd;
-ускорение точки D, его вектор отложен на плане ускорений в виде отрезка pd; -нормальное ускорение точки D во вращательном движение звена 4 относительно B, по модулю равное
-нормальное ускорение точки D во вращательном движение звена 4 относительно B, по модулю равное 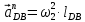 (направлено параллельно линии BD от точки D к точке B)
(направлено параллельно линии BD от точки D к точке B) -касательное ускорение точки D во вращательном движении звена 4 относительно точки B (направлено перпендикулярно линии ED)
-касательное ускорение точки D во вращательном движении звена 4 относительно точки B (направлено перпендикулярно линии ED)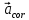 -кориолисово ускорение точки D в движении относительно звена 4, направление которого повернуто на 90 по
-кориолисово ускорение точки D в движении относительно звена 4, направление которого повернуто на 90 по 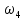 от VDE
от VDE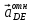 -ускорение точки D в поступательном движении звена 4 относительно точки E (сонаправлено вектору VDE)
-ускорение точки D в поступательном движении звена 4 относительно точки E (сонаправлено вектору VDE)Ускорение точек
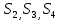 находим способом, аналогичным способу нахождения их скоростей. Для нахождения ускорения точки
находим способом, аналогичным способу нахождения их скоростей. Для нахождения ускорения точки 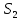 построим на векторе ab точку
построим на векторе ab точку 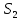
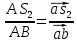
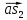 =
= 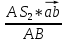 =
=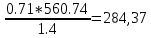
И проведем вектор
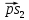
, который будет определять ускорение точки s2. Определим длину и найдем расчетное значение:
 2 = 122,42,
2 = 122,42, 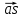 2=
2= 2*Ka=122,42*1
2*Ka=122,42*1Аналогично образом найдем ускорения точки
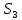 и S4. S3 на векторе pb, S4 на векторе bd.
и S4. S3 на векторе pb, S4 на векторе bd.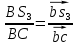
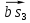 =
=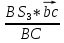 =
= 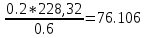 мм
мм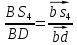
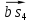 =
=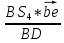 =
= 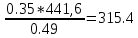 мм
мм S3=
S3= 3*Ka=190.99*1 = 190.33 м/
3*Ka=190.99*1 = 190.33 м/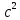
 S4=
S4= 4*Ka=158.11*1 = 159.11 м/
4*Ka=158.11*1 = 159.11 м/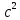
Таблица 4 – результаты вычислений ускорений точек, угловых ускорений звеньев.
| Положение величин | Размеры на чертеже,мм | Ускорения точек,м/c^2 |
| 1 | 1 | |
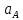 | 367.5 | 367.5 |
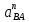 | 0.56 | 0.56 |
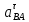 | 560.74 | 560.74 |
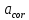 | 202.04 | 202.04 |
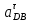 | 417.15 | 417.15 |
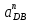 | 144.9 | 144.9 |
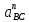 | 185.8 | 185.8 |
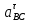 | 132.7 | 132.7 |
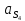 | 158,11 | 158,11 |
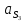 | 190,99 | 190,99 |
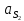 | 121,45 | 121,45 |