ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 78
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2.2 Содержательная постановка задачи
2.3 Математическая постановка задачи классификации с пересекающимися классами
2.4 Адаптация выбранного математического аппарата для решения задач ВКР
2.6 Выбор IT-инструментария для разработки программного обеспечения
2.8 Разработанное основное алгоритмическое обеспечение
Оглавление
2 СПЕЦАЛЬНАЯ ЧАСТЬ 2
2.1 Описание исходных данных 2
2.2 Содержательная постановка задачи 3
2.3 Математическая постановка задачи классификации с пересекающимися классами 4
2.4 Адаптация выбранного математического аппарата для решения задач ВКР 6
2.5 Пример исходных данных 9
2.6 Выбор IT-инструментария для разработки программного обеспечения 14
2.7 Техническое обеспечение 15
2.8 Разработанное основное алгоритмическое обеспечение 20
2.9 Разработанное программное обеспечение 28
2.10 Результаты 31
2.11 Анализ результатов 35
Список литературы 36
2 СПЕЦАЛЬНАЯ ЧАСТЬ
2.1 Описание исходных данных
Облачные сервисы обеспечивают предоставление вычислительных услуг, таких как хранилища, базы данных, сети и обработка данных через интернет, а не на локальном сервере или персональном компьютере. “Облаком” называют платформу для размещения вычислительных ресурсов, а также ресурсов хранения. Это так называемый виртуализированный центр обработки данных, который доступен для аренды за установленную плату.
Облачные сервисы являются экономически более эффективными, чем традиционные центры обработки данных. Многие крупные организации по всему миру используют систему облачных вычислений для решения задач, связанных с управлением данными, сокращения инфраструктурных инвестиций и расходов на обслуживание.
Концепция Ставится задача разрабатываемого программного продукта представляет собой настольное приложение, реализующее технологию блокчейн и уменьшающее выявленные недостатки аналогичных продуктов. Для решения проблемы связанной с уменьшением децентрализации сети из-за большой концентрации вычислительной ASIC-мощности у отдельных узлов цепи было решено использовать в качестве криптографичческой функции адаптивную хеш-функцию SCrypt, разработанную в 2012 году Колином Персивалем. Функция хэшинга SCrypt специально разрабатывалась с целью усложнить аппаратные реализации путем использования значительных объёмов пямяти со случайным доступом, например ОЗУ компьютеров. По причине высоких требований к памяти ASIC-оборудование не будет так же эффективно для майнинга. Вычислительная мощность в такой сети будет распределена более равномерно, среди её узлов, благодаря чему система останется децентрализованной. Для сокращения времени исполнения транзакций скорость добавления нового блока в систему была уменьшена до 2 минут, но для предотвращения ошибки двойных трат и сохранения безопасности цепи минимальная глубина блока для исполнения транзакции, находящейся в этом блоке будет равна 5. Это позволит сократить минимальное время подтверждения транзакции до 10-12 минут.
2.2 Содержательная постановка задачи
Сеть в системе блокчейн может насчитывать тысячи компьютеров. Полная децентрализация такой сети приведёт к сложностям в управлении ими. Поэтому для разрабатываемого приложения предлагается гибридная архитектура сети (рисунок 2.1).
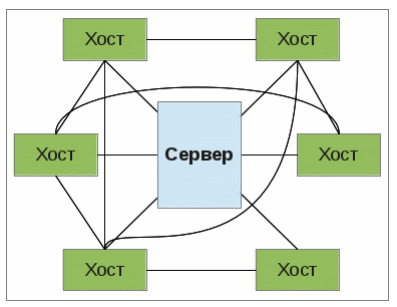
Рисунок 2.1 – Гибридная сеть
Координационный сервер выполняет задачи контроля за состоянием сети и предоставления списка активных участников сети.
Функционал разрабатываемого приложения состоит из следующих модулей: - Модуль User interface обеспечивает передачу информации между пользователем и программными компонентами приложения.
- Модуль Blockchain core отвечает за выполнение всех основных операций.
- Модуль Serialization отвечает за сериализацию данных для передачи и приёма данных в сети. - Модуль P2PServer выполняет основные функции по обработке и приёму данных от других узлов сети. - Модуль P2PClient отвечает за отправку данных всем активным участникам сети.
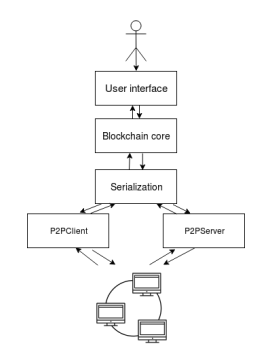
Рисунок 2.2 — Модули приложения и связи между ними
2.3 Математическая постановка задачи классификации с пересекающимися классами
При решении задачи распознавания объектов, принадлежащих пересекающимся классам, успешно применяются нейронные нечёткие продукционные сети, соединяющие возможности систем нечёткого вывода и нейронных сетей. Базовой моделью нечёткого вывода является модель Мамдани—Заде [1, 2],
однако широкое распространение получила только одна нечёткая продукционная нейронная сеть — сеть Ванга—Менделя [3–5], которая была создана на её основе. Применение сети Ванга—Менделя для решения задачи классификации вызывает определённые трудности. Во-первых, традиционная архитектура сети предполагает один выходной нейрон, что приводит к увеличению погрешности классификации при увеличении числа распознаваемых классов. Во-вторых, в сети Ванга—Менделя не предусмотрена модификация интерпретаций нечётких логических операций, реализующих нечёткие продукционные правила вывода.
В [6] описана и исследована предложенная авторами многовыходовая модификация сети Ванга—Менделя. В данной статье предлагается новая архитектура нейронной нечёткой продукционной сети, основанной на модели Мамдани—Заде, и исследуется решение задачи классификации для предложенной нечёткой сети и сети Ванга—Менделя с несколькими выходами при интерпретациях нечётких логических операций в соответствии в алгебрами Гёделя, Гогена и Лукашевича. Типовая структура системы нечёткого вывода включает в себя блок фаззификации, базу нечётких правил вывода, модуль вывода решения и блок дефаззификации. Фаззификатор преобразует чёткое множество входных данных
в нечёткое множество A ⊆ X, определённое с помощью конкретной функции принадлежности µA(x); здесь
Дефаззификатор преобразует несколько нечётких множеств Bk , k = 1, 2, . . . , M, или единственное нечёткое множество B в конкретное значение выходной переменной y ∈ Y на основании нечётких выводов, вырабатываемых модулем вывода решений, и в соответствии с выбранным методом дефаззификации (символами X и Y обозначаются пространства входных и выходных переменных). Подобная система также может быть представлена в несколько ином виде, в частности на рис. 1 [5]. Выходной сигнал модуля вывода решений может иметь вид M нечётких множеств, определяющих диапазон изменения выходной переменной.
Агрегатор преобразует M нечётких множеств в одно нечёткое множество, а дефаззификатор преобразует это множество в одно конкретное значение, принимаемое в качестве выходного сигнала всей системы. В модели вывода Мамдани—Заде присутствуют следующие операции [5]: – операция логического или арифметического произведения для определения значения функции принадлежности условий правил, в которой учитываются все компоненты вектора условия; – операция логического или арифметического произведения для определения значения функции принадлежности для всей импликации Ak→Bk ; – операция логической суммы для агрегации равнозначных результатов импликации многих правил; – оператор дефаззификации, трансформирующий нечёткий результат
µB0(y) в чёткое значение y. Считается, что все M правил связаны между собой логической операцией «ИЛИ», а выходы правил y 1 , y2 , . . . , yM взаимно независимы. Следовательно, можно использовать правила вида:
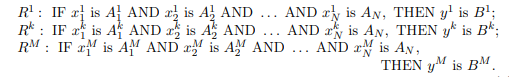
2.4 Адаптация выбранного математического аппарата для решения задач ВКР
Асимметричная криптография, также известная как криптография с открытым ключом, использует общедоступные и закрытые ключи для шифрования и дешифрования данных. Ключи - это просто большие числа, которые были соединены вместе, но не идентичны (асимметричны). Один ключ из пары может быть известен всем, он называется открытым ключом. Другой ключ из пары хранится в секрете, он называется закрытым ключом. Любой из ключей может использоваться для шифрования сообщения; для дешифрования используется противоположный ключ от того, который используется для шифрования сообщения. Многие протоколы, такие как SSH, OpenPGP, S/MIME и SSL/TLS, основаны на асимметричной криптографии для функций шифрования и цифровой подписи.
Он также используется в программах, таких как браузеры, которым необходимо установить безопасное соединение по небезопасной сети, например, в Интернете, или для проверки цифровой подписи. Надёжность шифрования напрямую зависит от размера ключа, а удвоение длины ключа обеспечивает экспоненциальное увеличение прочности, хотя и снижает 17 производительность. По мере увеличения вычислительной мощности и выявления более эффективных алгоритмов факторинга увеличивается и способность увеличивать и увеличивать число также возрастает. При асимметричном шифровании для обеспечения конфиденциальности, целостности, аутентичности и отказоустойчивости, пользователи и системы должны быть уверены, что открытый ключ является подлинным, что он принадлежит заявленному лицу или субъекту и что он не был подделан или заменен злоумышленниками. Не существует идеального решения проблемы аутентификации с открытым ключом.
Наиболее распространенным подходом является инфраструктура открытых ключей (PKI), в которой доверенные сертификационные центры сертифицируют права собственности на пары ключей и сертификаты, но продукты шифрования, основанные на модели Pretty Good Privacy (включая OpenPGP), полагаются на децентрализованную модель аутентификации, называемой веб-службой доверия, которая опирается на индивидуальные одобрения связи между пользователем и открытым ключом. Уитфилд Диффи и Мартин Хеллман, исследователи из Стэнфордского университета, впервые публично предложили асимметричное шифрование в своей статье 1977 года «Новые направления в криптографии». За несколько лет до Диффи и Хеллмана эта концепция была независимо и
секретно предложена Джеймсом Эллисом, который работал в штаб-квартире правительственных коммуникаций (GCHQ), британской разведывательной и охранной организации.
Асимметричный алгоритм, описанный в документе ДиффиХеллмана, использует специальные числа, для создания ключей дешифрования. RSA (Rivest-Shamir-Adleman), наиболее широко используемый асимметричный алгоритм, встроен в протокол SSL/TLS, который используется для обеспечения безопасности связи по компьютерной сети. RSA получает свою безопасность от вычислительной сложности факторизации больших целых чисел, которые являются произведением двух больших простых чисел. Умножение двух больших простых чисел легко, но сложность определения исходных чисел из суммарного факторинга - является основой безопасности 18 криптографии с открытым ключом.
Время, затрачиваемое на фактор продукта двух достаточно больших простых чисел, считается слишком большим для основной части атакующих, за исключением национальных государственных субъектов, которые могут иметь доступ к достаточной вычислительной мощности. RSA-ключи обычно имеют длину 1024 или 2048 бит, но эксперты считают, что в ближайшем будущем могут быть взломаны 1024-битные ключи, поэтому правительство и индустрия переходят на минимальную длину ключа 2048 бит[7]. Эллиптическая кривая криптографии (ECC) завоевывает популярность у многих экспертов по безопасности в качестве альтернативы
RSA для реализации криптографии с открытым ключом. ECC - это метод шифрования с открытым ключом, основанный на теории эллиптических кривых, который может создавать более быстрые, более мелкие и более эффективные криптографические ключи. ECC генерирует ключи через свойства уравнения эллиптической кривой. Чтобы взломать ECC, нужно вычислить дискретный логарифм эллиптической кривой, и оказывается, что это значительно более сложная задача, чем факторинг.
В результате размеры ключей ECC могут быть значительно меньше, чем требуемые RSA, но обеспечивают эквивалентную безопасность с меньшей вычислительной мощностью и потреблением ресурсов батареи