Добавлен: 30.11.2023
Просмотров: 95
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2. Задача. Исследование зависимости содержания ионов от плотности пластовой воды
2.4 Вычисление прогнозного значения
3. Расчеты для определения коэффициентов зависимости и
3.1 Расчеты для "общего" уравнения
3.2 Расчеты для "специализированного" уравнения
3.3 Вычисление прогнозного значения
4.3 Вычисление прогнозного значения
5. Расчеты для определения коэффициентов зависимости и
5.1 Расчеты для "общего" уравнения
2. Задача. Исследование зависимости содержания ионов от плотности пластовой воды
Специализированное уравнение
Вбиваем исходные данные в ячейки. Рассчитываем приведенную плотность для нахождения и сравнения графиков приведённой и данной плотности.
| Плотность | Содержание ионов Cl- | Приведенная плотность | | |
| ro | c | ro' | | |
| X | Y | Z=X-1000 | Z*Z | Z*Y |
| 1015,0 | 380,8 | 15,0 | 225 | 5711,4 |
| 1033,0 | 723,6 | 33,0 | 1089 | 23878,1 |
| 1034,0 | 901,6 | 34,0 | 1156 | 30655,8 |
| 1044,0 | 881,5 | 44,0 | 1936 | 38786,9 |
| 1054,0 | 1196,4 | 54,0 | 2916 | 64605,6 |
| 1063,0 | 1378,3 | 63,0 | 3969 | 86831,6 |
| 1074,0 | 1751,2 | 74,0 | 5476 | 129585,8 |
| 1091,0 | 2312,9 | 91,0 | 8281 | 210475,7 |
| 1095,0 | 2389,9 | 95,0 | 9025 | 227042,4 |
| 1095,0 | 2464,8 | 95,0 | 9025 | 234156,0 |
| 1107,0 | 2778,7 | 107,0 | 11449 | 297318,8 |
| 1111,0 | 2825,7 | 111,0 | 12321 | 313650,5 |
| 1119,0 | 3025,6 | 119,0 | 14161 | 360041,6 |
| 1123,0 | 3264,6 | 123,0 | 15129 | 401540,9 |
| 1123,0 | 3320,5 | 123,0 | 15129 | 408421,5 |
| 1128,0 | 3370,4 | 128,0 | 16384 | 431416,3 |
| 1133,0 | 3374,4 | 133,0 | 17689 | 448792,5 |
| 1140,0 | 3743,3 | 140,0 | 19600 | 524064,8 |
| 1149,0 | 3644,3 | 149,0 | 22201 | 542994,7 |
| 1151,0 | 3779,2 | 151,0 | 22801 | 570659,2 |
| 1155,0 | 4148,1 | 155,0 | 24025 | 642961,7 |
| 1161,0 | 4010,1 | 161,0 | 25921 | 645622,9 |
| 1164,0 | 4125,0 | 164,0 | 26896 | 676503,3 |
| 1169,0 | 4478,0 | 169,0 | 28561 | 756775,2 |
| 1175,0 | 4536,9 | 175,0 | 30625 | 793957,5 |
Рисунок 1 - Исходные данные для построения эмпирической зависимости и расчет “приведенной” плотности.
| Плотность | Содержание ионов Cl- | Приведенная плотность | | |
| ro | c | ro' | | |
| X | Y | Z=X-1000 | Z*Z | Z*Y |
| 1015 | 380,76 | =B7-1000 | =D7^2 | =D7*C7 |
| 1033 | 723,58 | =B8-1000 | =D8^2 | =D8*C8 |
| 1034 | 901,64 | =B9-1000 | =D9^2 | =D9*C9 |
| 1044 | 881,52 | =B10-1000 | =D10^2 | =D10*C10 |
| 1054 | 1196,4 | =B11-1000 | =D11^2 | =D11*C11 |
| 1063 | 1378,28 | =B12-1000 | =D12^2 | =D12*C12 |
| 1074 | 1751,16 | =B13-1000 | =D13^2 | =D13*C13 |
| 1091 | 2312,92 | =B14-1000 | =D14^2 | =D14*C14 |
| 1095 | 2389,92 | =B15-1000 | =D15^2 | =D15*C15 |
| 1095 | 2464,8 | =B16-1000 | =D16^2 | =D16*C16 |
| 1107 | 2778,68 | =B17-1000 | =D17^2 | =D17*C17 |
| 1111 | 2825,68 | =B18-1000 | =D18^2 | =D18*C18 |
| 1119 | 3025,56 | =B19-1000 | =D19^2 | =D19*C19 |
| 1123 | 3264,56 | =B20-1000 | =D20^2 | =D20*C20 |
| 1123 | 3320,5 | =B21-1000 | =D21^2 | =D21*C21 |
| 1128 | 3370,44 | =B22-1000 | =D22^2 | =D22*C22 |
| 1133 | 3374,38 | =B23-1000 | =D23^2 | =D23*C23 |
| 1140 | 3743,32 | =B24-1000 | =D24^2 | =D24*C24 |
| 1149 | 3644,26 | =B25-1000 | =D25^2 | =D25*C25 |
| 1151 | 3779,2 | =B26-1000 | =D26^2 | =D26*C26 |
| 1155 | 4148,14 | =B27-1000 | =D27^2 | =D27*C27 |
| 1161 | 4010,08 | =B28-1000 | =D28^2 | =D28*C28 |
| 1164 | 4125,02 | =B29-1000 | =D29^2 | =D29*C29 |
| 1169 | 4477,96 | =B30-1000 | =D30^2 | =D30*C30 |
| 1175 | 4536,9 | =B31-1000 | =D31^2 | =D31*C31 |
Рисунок 2- Исходные данные для построения эмпирической зависимости и расчет “приведенной” плотности. Режим отображения формул.
Находим сумму и среднего значения по X и Y, так как они понадобятся в дальнейших вычислениях. Вычислим коэффициент корреляции из данных значений X и Y.
| Сумма | 27706,0 | 68805,7 |
| Ср.знач. | 1108,2 | 2752,2 |
| | | |
| | r= | 0,99599 |
Рис 3-Вычисление сумм и коэфициета корреляции.
| Сумма | =СУММ(B7:B31) | =СУММ(C7:C31) |
| Ср.знач. | =СРЗНАЧ(B7:B31) | =СРЗНАЧ(C7:C31) |
| | | |
| | r= | =КОРРЕЛ(B7:B31;C7:C31) |
Рисунок 4-Вычисление сумм и коэффициента корреляции. Режим отображения формул.
Производим расчеты для специализированного уравнения. Для этого мы вычисляем
-
квадрат “приведённой” плотности и ее сумму; -
произведение “приведённой” плотности на значения Y и их сумму; -
разность каждого значения Y и среднего значения Y рассчитанного ранее и их сумму квадрат разницы, суммой которого является полная сумма; -
Рассчитываем Y теоретическое, для этого значение коэффициента с умножаем на вычисляемую разность от х -1000.
Для дальнейших действий рассчитываем коэффициент с, равный отношению сумм произведения “приведённой” плотности на Y, и квадрата “приведённой” плотности.
-
Вычисляем разность Y теоретического и Y; -
Возводим в квадрат разность, сумма каждого значения будет являться суммой остатка; -
Разность Y теоретического и Y среднего значения, возведение его в квадрат, сумма которой обозначается регрессивной.
Вычисляем
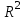 ,для этого отнимем от единицы отношение суммы остатка, деленное на сумму полную.
,для этого отнимем от единицы отношение суммы остатка, деленное на сумму полную. Мы нашли значение с и R^2.
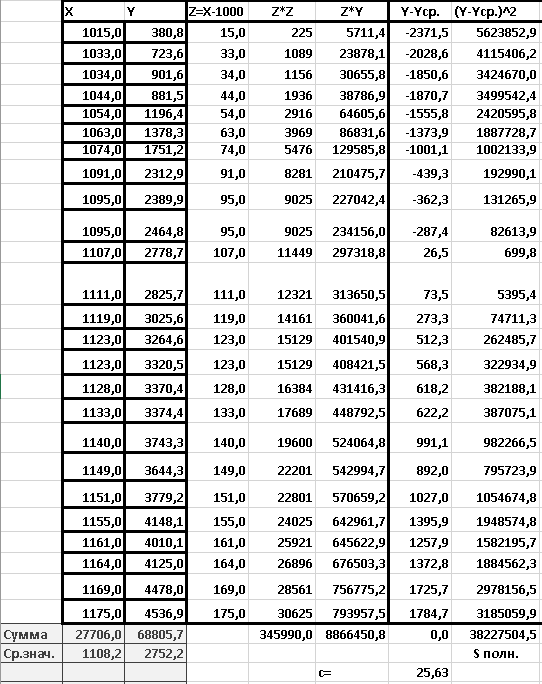
Рисунок 5 - Вычисление формул для специализированного уравнения. Нахождение значений с и R^2.
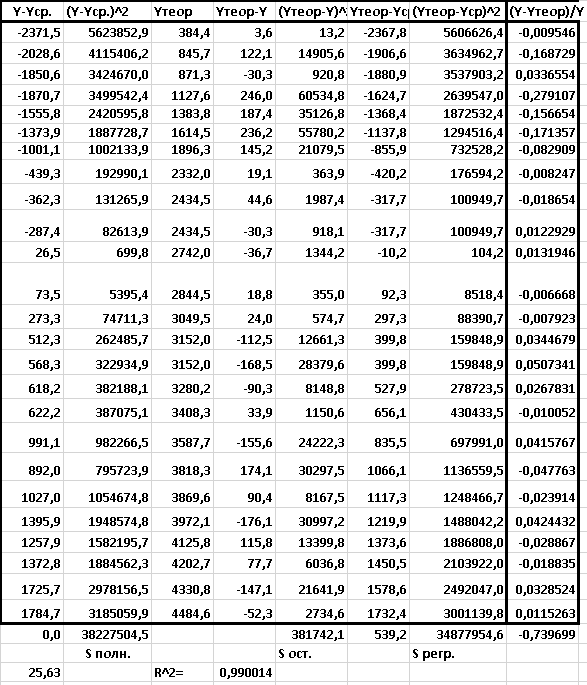
Рисунок 6 - Вычисление формул для специализированного уравнения. Нахождение значений с и R^2.
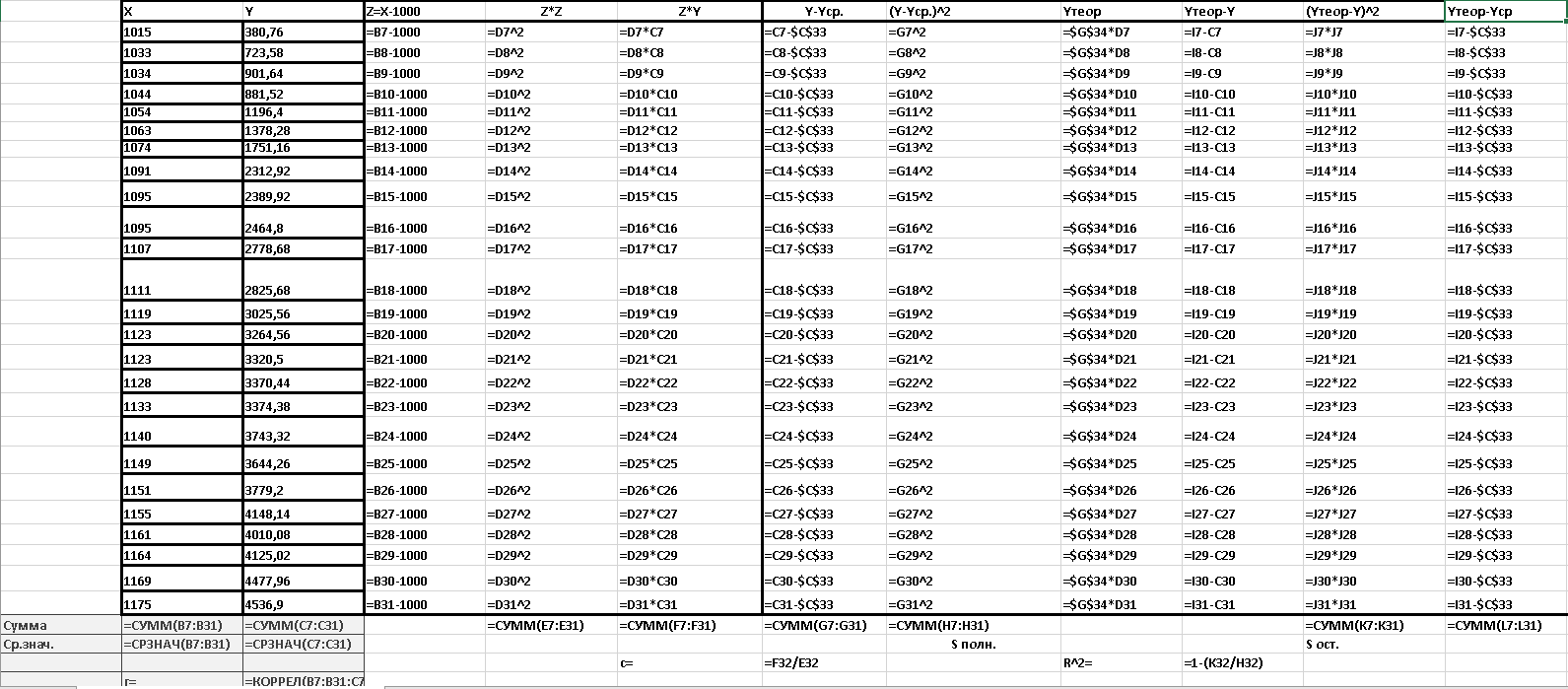
Рисунок 7 - Вычисление формул для специализированного уравнения. Нахождение значений с и R^2.Режим отображения формул.
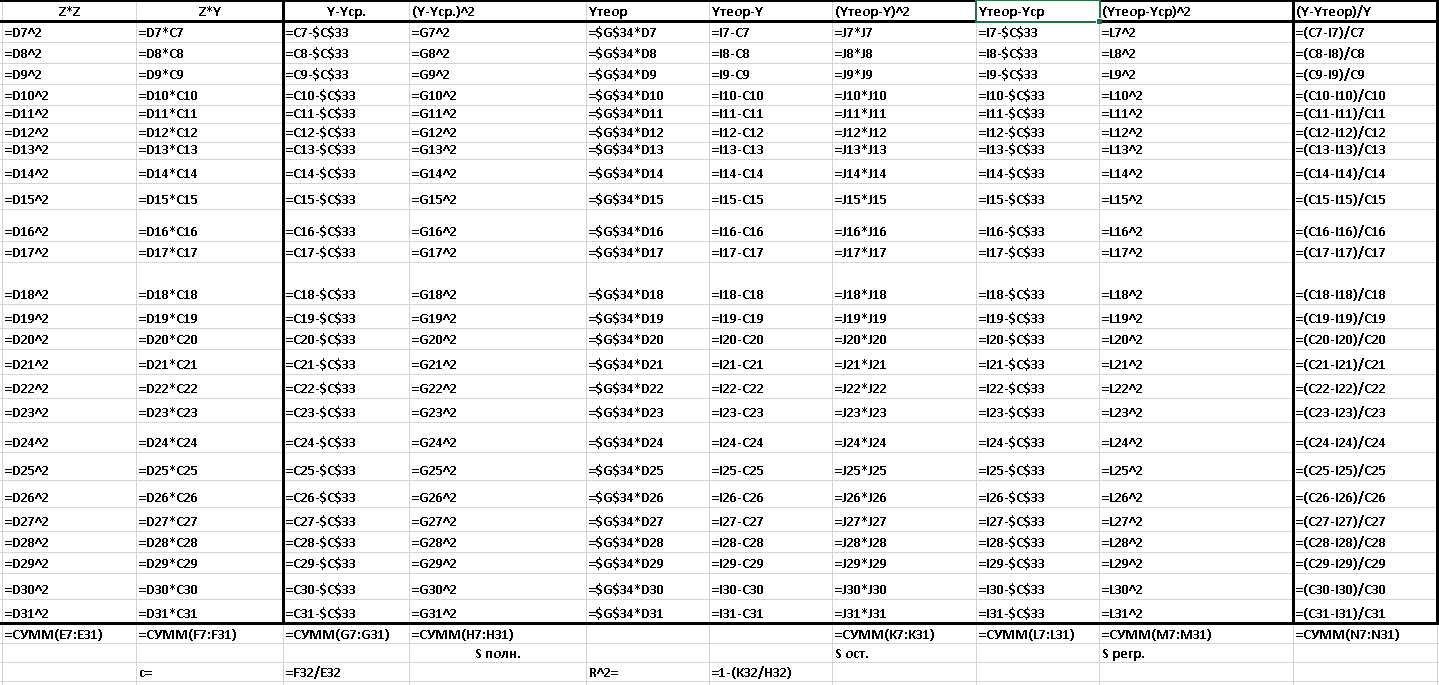
Рисунок 8 - Вычисление формул для специализированного уравнения. Нахождение значений с и R^2.Режим отображения формул.
2.2 Уравнение общего вида.
В этом способе решения вычисляем значения:
-
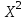 , произведение X и Y и находим сумму этих элементов с помощью функции СУММ.
, произведение X и Y и находим сумму этих элементов с помощью функции СУММ. -
Вычисляем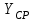 помощью функции СР.ЗНАЧ. Находим разницу значений н Y н
помощью функции СР.ЗНАЧ. Находим разницу значений н Y н 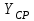 ,находим сумму всех элементов, она будет равна нулю. Квадрат этих значений и последующая вычисленная их сумма будут являться суммой полной.
,находим сумму всех элементов, она будет равна нулю. Квадрат этих значений и последующая вычисленная их сумма будут являться суммой полной. -
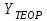 вычисляем так :коэффициент
вычисляем так :коэффициент 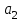 из матричного метода умножаем на Х и прибавляем второй корень
из матричного метода умножаем на Х и прибавляем второй корень 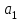 , вычисляем сумму. Находим квадрат каждого элемента и общую сумму, она и будет являться суммой остатка
, вычисляем сумму. Находим квадрат каждого элемента и общую сумму, она и будет являться суммой остатка -
Сумму регрессивную находим из таких вычислений: сначала, вычисляем значения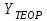 -
- 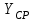 ,их квадрат, именно квадрат их суммы будет являться регрессивной.
,их квадрат, именно квадрат их суммы будет являться регрессивной.
Создаем матрицу А элемент
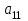 который равен количеству значений X и Y,
который равен количеству значений X и Y, 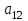 и
и 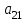 равен сумме всех значении X рассчитанного на первых этапах вычислений
равен сумме всех значении X рассчитанного на первых этапах вычислений 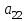 равен сумме квадрата значений. Матрица B состоит из элемента
равен сумме квадрата значений. Матрица B состоит из элемента 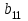 сумма всех значений переменной Y,и
сумма всех значений переменной Y,и 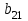 соответствует сумме всех значений произведения переменных X и Y.
соответствует сумме всех значений произведения переменных X и Y.С помощью матричного метода получаем значения
 и
и  .Находим коэффициент
.Находим коэффициент