Добавлен: 30.11.2023
Просмотров: 88
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2. Задача. Исследование зависимости содержания ионов от плотности пластовой воды
2.4 Вычисление прогнозного значения
3. Расчеты для определения коэффициентов зависимости и
3.1 Расчеты для "общего" уравнения
3.2 Расчеты для "специализированного" уравнения
3.3 Вычисление прогнозного значения
4.3 Вычисление прогнозного значения
5. Расчеты для определения коэффициентов зависимости и
5.1 Расчеты для "общего" уравнения
Рисунок 22 - Вычисление некоторых характеристик эмпирических данных.
3.1 Расчеты для "общего" уравнения
Способ №1. Вычисление коэффициентов «общего" уравнения, с помощью решения нормальной системы уравнений.
Для нахождения коэффициентов рассчитываем:
Сумму всех значений X,Y,произведения X*Y и X*X,с помощью функции S.
Создаем матрицу А: элементом
 - является количество неизвестных N;
- является количество неизвестных N;  ,
, а-сумма по X;
а-сумма по X;  -сумма всех значений произведения X.И массив B : элемент с индексом
-сумма всех значений произведения X.И массив B : элемент с индексом  - сумма по Y;
- сумма по Y; -сумма всех значений произведения XY.Решаем матрицу матричным методом. Коэффициент
-сумма всех значений произведения XY.Решаем матрицу матричным методом. Коэффициент  и
и равны произведению обратной матрицы A на массив В.
равны произведению обратной матрицы A на массив В.
Рисунок 23 - Расчеты для “общего” уравнения
Способ №2. Вычисление коэффициентов «общего" уравнения, с помощью
функции line.
Для проведения линейной регрессии по методу МНК выбираем функцию line (X, Y). Параметры данной функции уже полученные нами ранее массивы значений. Результатом функции line будет вектор, содержащий значения параметров, а и b, такие параметры, при которых прямая y=a+bx наилучшим способом аппроксимировала заданный набор точек. Получаем два корня.
Записываем “общее’ уравнение в явном виде и находим
 .
.Вычисляем коэффициент детерминации

для "общего” уравнения. Определяем сумму остатка с помощью функции resid.Для этого от каждого значения Yотнимаем
 .,возводим в квадрат и суммируем каждый элемент.
.,возводим в квадрат и суммируем каждый элемент.Находим коэффициент детерминации для "общего" уравнения. Он равен разнице единицы и частного суммы остатка на полную сумму.
Записываем общее уравнение в общем виде.

Рисунок 24 - Вычисление коэффициентов «общего" уравнения, с помощью
функции line.
3.2 Расчеты для "специализированного" уравнения
Рассчитываем новый массив Z равные разнице значения X и 1000.
Находим сумму всех значений произведения Z*Z, Z*Yс помощью функции S.
Определяем коэффициент с, равный частному сумм всех значений произведения Z*Y на Z*Z.
Записываем специализированное уравнение в общем виде. Определяем теоретические значения Y для "специализированного" уравнения.
Вычисляем коэффициент детерминации
 для "специализированного" уравнения :для этого вычисляем сумму остаточную всех значений для спец. уравнения, то есть, находим квадрат разности каждого элемента Y и
для "специализированного" уравнения :для этого вычисляем сумму остаточную всех значений для спец. уравнения, то есть, находим квадрат разности каждого элемента Y и  специализированного. Коэффициент детерминации для специализированного уравнения равен разнице единицы от частной суммы остатка всех значений для спец. Уравнения на сумму полную.
специализированного. Коэффициент детерминации для специализированного уравнения равен разнице единицы от частной суммы остатка всех значений для спец. Уравнения на сумму полную.Строим аппроксимирующий график.

Рисунок 25 - Расчеты для "специализированного" уравнения
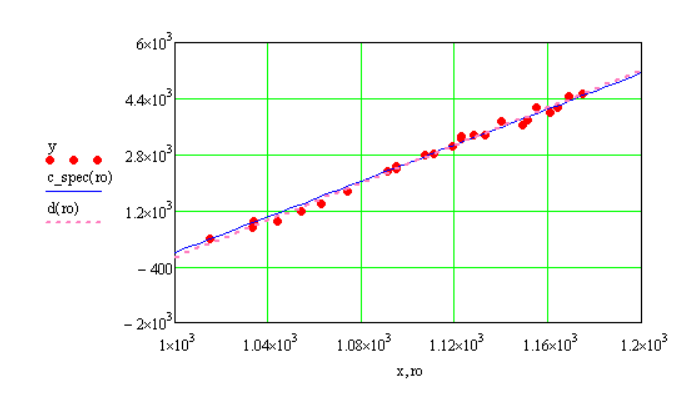
Рисунок 26 - Аппроксимирующий график.
3.3 Вычисление прогнозного значения
При помощи функции prognoz находим X прогнозное специализированного и общего уравнений.
Вычисляем разницу абсолютную, для этого от X прогнозного из общего уравнения отнимаем X прогноз. специализированного. Относительная разница равна отношению абсолютной разницы на X прогноз.

Рисунок 27 – Вычисление прогнозного значения
4. Задача. Исследование зависимости насыщения подземных вод газом от глубины залегания водоносных горизонтов.
4.1 Уравнение общего вида.
В этом способе решения вычисляем значения:
-
 , произведение X и Y и находим сумму этих элементов с помощью функции СУММ.
, произведение X и Y и находим сумму этих элементов с помощью функции СУММ. -
Вычисляем помощью функции СР.ЗНАЧ. Находим разницу значений н Y н
помощью функции СР.ЗНАЧ. Находим разницу значений н Y н  ,находим сумму всех элементов, она будет равна нулю. Квадрат этих значений и последующая вычисленная их сумма будут являться суммой полной.
,находим сумму всех элементов, она будет равна нулю. Квадрат этих значений и последующая вычисленная их сумма будут являться суммой полной. -
 вычисляем так :коэффициент
вычисляем так :коэффициент  из матричного метода умножаем на Х и прибавляем второй корень
из матричного метода умножаем на Х и прибавляем второй корень  , вычисляем сумму. Находим квадрат каждого элемента и общую сумму, она и будет являться суммой остатка
, вычисляем сумму. Находим квадрат каждого элемента и общую сумму, она и будет являться суммой остатка -
Сумму регрессивную находим из таких вычислений: сначала, вычисляем значения -
-  ,их квадрат, именно квадрат их суммы будет являться регрессивной.
,их квадрат, именно квадрат их суммы будет являться регрессивной.
Создаем матрицу А элемент
 который равен количеству значений X и Y,
который равен количеству значений X и Y,  и
и  равен сумме всех значении X рассчитанного на первых этапах вычислений
равен сумме всех значении X рассчитанного на первых этапах вычислений  равен сумме квадрата значений. Матрица B состоит из элемента
равен сумме квадрата значений. Матрица B состоит из элемента  сумма всех значений переменной Y,и
сумма всех значений переменной Y,и  соответствует сумме всех значений произведения переменных X и Y.С помощью матричного метода получаем значения
соответствует сумме всех значений произведения переменных X и Y.С помощью матричного метода получаем значения  и
и  .Находим коэффициент
.Находим коэффициент ,для того отнимем от единицы отношение суммы остатка деленную на сумму полную.
,для того отнимем от единицы отношение суммы остатка деленную на сумму полную. 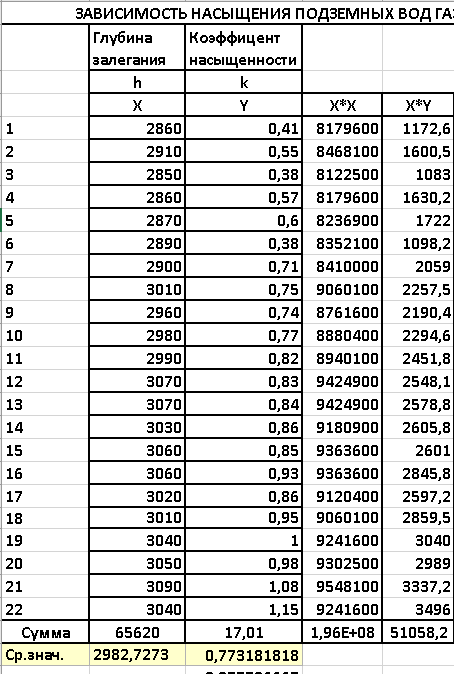
Рисунок 28 - Расчеты для уравнения общего вида. Нахождение коэффициентов.
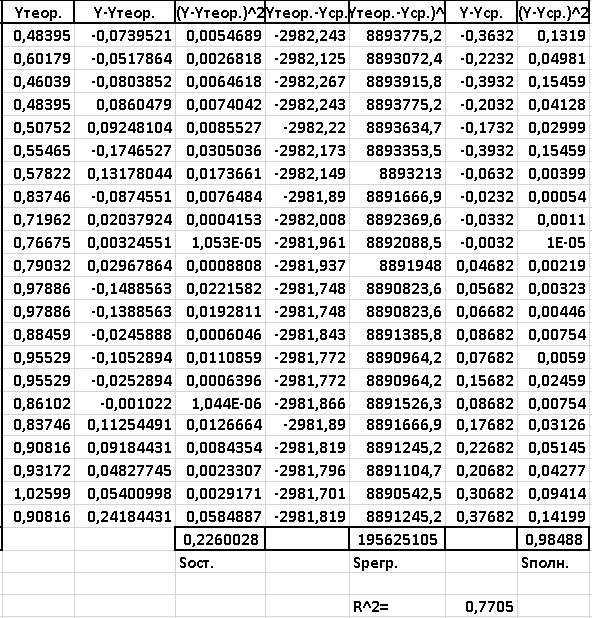
Рисунок 29 - Расчеты для уравнения общего вида. Нахождение коэффициентов.
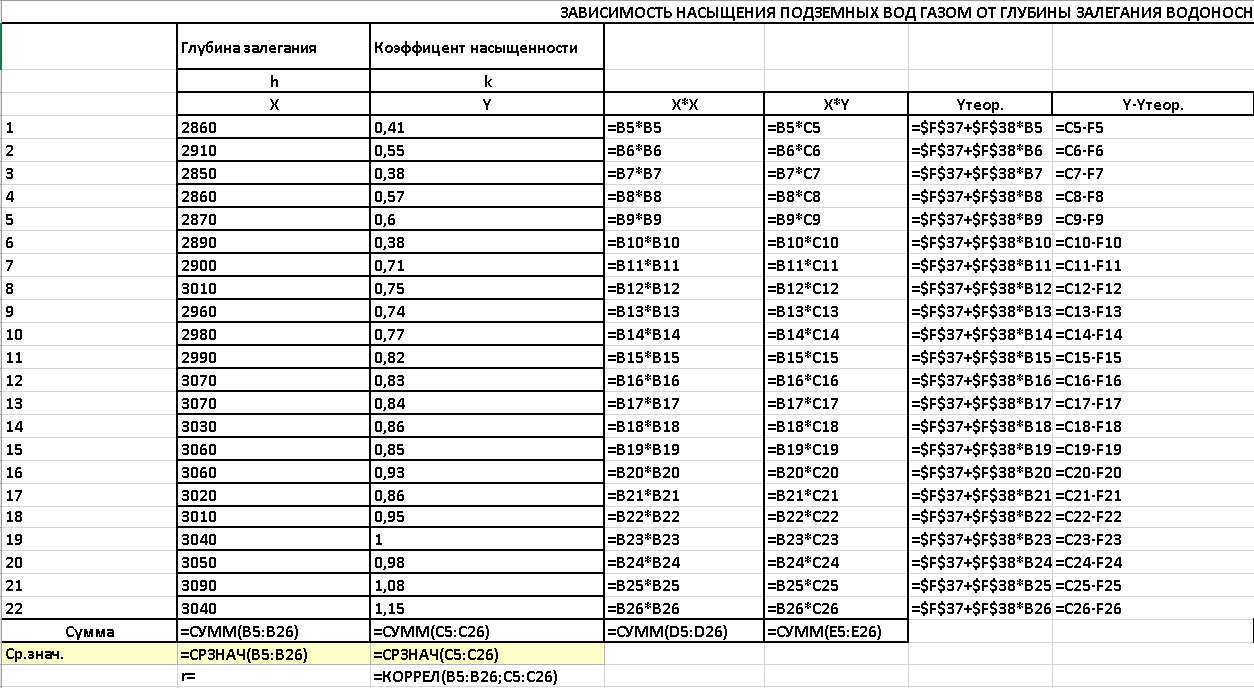
Рисунок 30 - Расчеты для уравнения общего вида. Нахождение коэффициентов. Режим отображения формул.
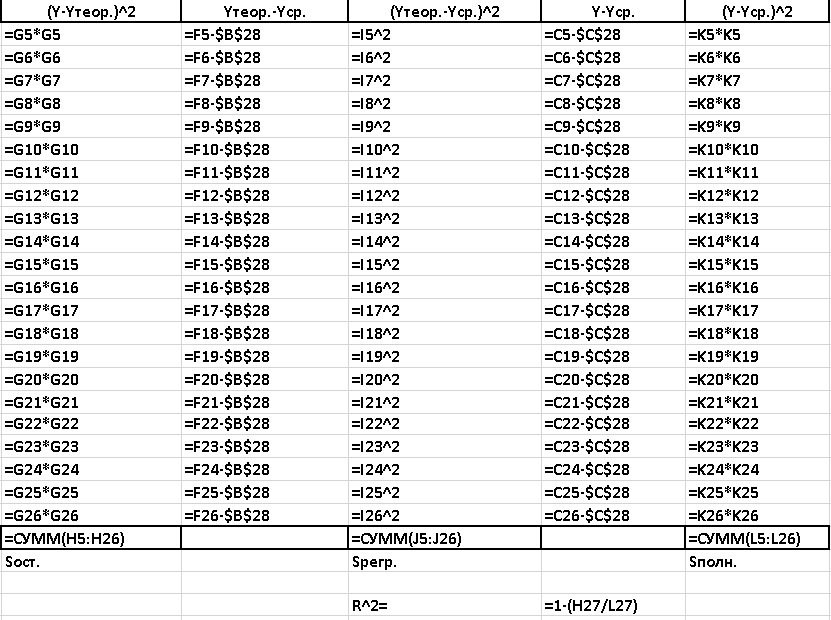
Рисунок 31 - Расчеты для уравнения общего вида. Нахождение коэффициентов. Режим отображения формул.
| A | | | B | |
| 22 | 65620 | | 17,01 | |
| 65620 | 195863200 | | 51058,2 | |
| | | | | |
| A^(-1) | | | | |
| 65,1574185 | -0,021829674 | | a | -6,25617 |
| -0,02182967 | 7,3187E-06 | | b | 0,002357 |
Рисунок 32 - Решение матрицы. Нахождение коэффициентов.
| A | | | B | |
| =A26 | =B27 | | =C27 | |
| =B27 | =D27 | | =E27 | |
| | | | | |
| A^(-1) | | | | |
| =МОБР(B33:C34)__=МОБР(B33:C34)'>=МОБР(B33:C34) | =МОБР(B33:C34) | | a | =МУМНОЖ(B37:C38;E33:E34) |
| =МОБР(B33:C34) | =МОБР(B33:C34) | | b | =МУМНОЖ(B37:C38;E33:E34) |
Рисунок 33 - Решение матрицы. Нахождение коэффициентов. Режим отображения формул.