Добавлен: 30.11.2023
Просмотров: 96
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2. Задача. Исследование зависимости содержания ионов от плотности пластовой воды
2.4 Вычисление прогнозного значения
3. Расчеты для определения коэффициентов зависимости и
3.1 Расчеты для "общего" уравнения
3.2 Расчеты для "специализированного" уравнения
3.3 Вычисление прогнозного значения
4.3 Вычисление прогнозного значения
5. Расчеты для определения коэффициентов зависимости и
5.1 Расчеты для "общего" уравнения
4.2 Произведение расчетов с помощью графика и линии тренда таблично заданной функции средствами табличного процессора Microsoft Excel
Для первого графика (с помощью вставка - точечная диаграмма) выбираем значения X и Y. Обозначаем оси, выбираем линию тренда. В работе с диаграммами - конструктор, выбираем формат линии тренда. Ставим галочки на нужные пункты (рис 34), выбираем цвет и тип линий. Программа автоматически выдаст коэффициент уравнение функции.

Рисунок 34 - Настройка параметров линии тренда.
Получены графики:
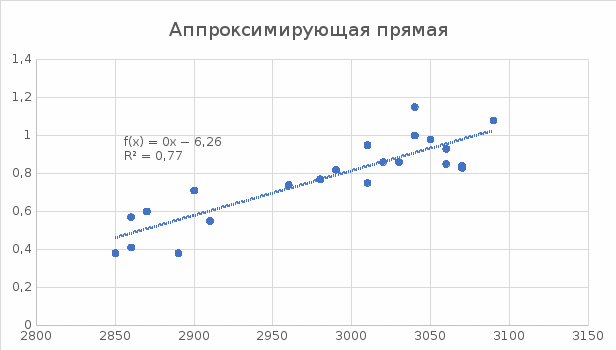
Рисунок 35 - Готовый график исследования.
4.3 Вычисление прогнозного значения
Находим X прогнозное. Для этого при помощи функции максимального значения от X и дальнейшего его разницы на 0.1 и произведения максимального и минимального значения X находим нужное выражение
| Вычисление прогнозного значения | | | |
| | X_прогноз | 3066 | |
| | | | |
| | Коэффициенты | | |
| Уравнения | а | b | y_прогноз |
| "Общее" | -6,25617166 | 0,002356687 | 0,9694295 |
Рисунок 36 - Вычисление прогнозного значения

Рисунок 37 - Вычисление прогнозного значения. Режим отображения формул.
Записываем значения коэффициентов из общего уравнения. Находим
 для общего :
для общего : умножаем на
умножаем на и добавляем
и добавляем .
. 5. Расчеты для определения коэффициентов зависимости и
с использованием MathCAD
Для ввода данных используется команда ►Вставка► Компонента из главного меню MathCAD. Будет запущен Мастер (специальная программа), который обеспечит выполнение всей процедуры ввода, результат ввода будет находиться в двумерном массиве W. Далее эти данные (по столбцам) присваиваем одномерным массивам X и Y, с которыми выполняем все дальнейшие операции.

Рисунок 38 - Решение задачи. Подготовка данных и запуск Мастера Компонентов для ввода данных в системе MathCAD.
Определяем начальный индекс с помощью ORIGIN. Вбиваем количество наблюдений используя rows. Устанавливаем пределы изменения индекса векторов: присваиваем значения от 1 до N (количество наблюдений). Эмпирические данные раскладываем по отдельным “векторам”-массивам X и Y. Выводим исходные данные, образуются два массива X и Y.
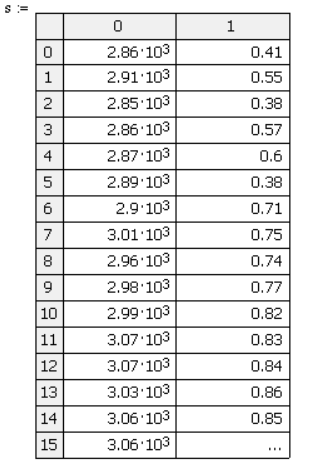
Рисунок 39 - Создание двумерного массива.

Рисунок 40 - Операции с массивом S.
Вычисляем некоторые характеристики эмпирических данных:
-
Вычисляем с помощью функции mean
с помощью функции mean -
Вычисляем сумму всех значений равных Y-
-
Находим минимальное и максимальное значение X помощью функции min и max -
Устанавливаем размах величины X, равный разности максимального и минимального значений X. -
Вычисляем прогнозное значение X ,при значении которого в дальнейших действиях вычислим . Для этого вычислим произведение X максимального на размах X.
. Для этого вычислим произведение X максимального на размах X. -
Находим коэффициент корреляции между величинами X и Y, используя функцию corr (X, Y).

Рисунок 41 - Вычисление некоторых характеристик эмпирических данных.
5.1 Расчеты для "общего" уравнения
Способ №1. Вычисление коэффициентов «общего" уравнения, с помощью решения нормальной системы уравнений.
Для нахождения коэффициентов рассчитываем:
Сумму всех значений X, Y, произведения X*Y и X*X, с помощью функции S.
Создаем матрицу А: элементом
 - является количество неизвестных N;
- является количество неизвестных N;  ,
, а-сумма по X;
а-сумма по X;  -сумма всех значений произведения X.И массив B : элемент с индексом
-сумма всех значений произведения X.И массив B : элемент с индексом  - сумма по Y;
- сумма по Y; -сумма всех значений произведения XY.Решаем матрицу матричным методом. Коэффициент
-сумма всех значений произведения XY.Решаем матрицу матричным методом. Коэффициент  и
и равны произведению обратной матрицы A на массив В.
равны произведению обратной матрицы A на массив В.
Рисунок 42 - Расчеты для “общего” уравнения
Способ №2. Вычисление коэффициентов «общего" уравнения, с помощью
функции line.
Для проведения линейной регрессии по методу МНК выбираем функци
Line (X, Y). Параметры данной функции уже полученные нами ранее массивы значений. Результатом функции line будет вектор, содержащий значения параметров, а и b, такие параметры, при которых прямая y=a+bx наилучшим способом аппроксимировала заданный набор точек. Получаем два корня.
Записываем “общее’ уравнение в явном виде и находим
 .
.Вычисляем коэффициент детерминации
 для "общего” уравнения. Определяем сумму остатка с помощью функции resid. Для этого от каждого значения Yотнимаем
для "общего” уравнения. Определяем сумму остатка с помощью функции resid. Для этого от каждого значения Yотнимаем
 .,возводим в квадрат и суммируем каждый элемент.
.,возводим в квадрат и суммируем каждый элемент.Находим коэффициент детерминации для "общего" уравнения. Он равен разнице единицы и частного суммы остатка на полную сумму.
Записываем общее уравнение в общем виде.

Рисунок 43 - Вычисление коэффициентов «общего" уравнения, с помощью
функции line.
5.2 Вычисление прогнозного значения
При помощи функции prognoz находим X прогнозное общего уравнения. Для этого коэффициент
 умножаем на
умножаем на и добавляем
и добавляем .
.
Рисунок 44 - Вычисление прогнозного значения
6. Выполнение задания на языке Pascal. Исследование зависимости насыщения подземных вод газом от глубины залегания водоносных горизонтов.
PascalABC.NET – мощный язык с простым и логичным синтаксисом, хорошо понятным начинающим программистам. Это позволяет писать компактные, эффективные и понятные программы и делает данный язык идеальным выбором для обучения современному программированию в широком смысле: от учеников начальной школы до студентов профильных ИТ-направлений. Кроме того, он превосходно подходит как для создания консольных приложений малого и среднего размера, так и в качестве средства программирования «на каждый день».
В var вводим переменные, которые будут учувствовать в этой программе. Задаем переменные. Присваиваем данным числовые и натуральные числовые значения

Рисунок 45 – Задание данных.
Begin – начало программы. X и y - два массива с 22 элементами, inputx, inputy, Text - переменные для данных. Командой assign и reset мы берём данные из сторонних файлов, в которых находятся наши массивы.

Рисунок 46 – Начало программы. Задание сторонних файлов, в которых находятся массивы.
Находим все данные, необходимые для нахождения всех коэффициентов и прогнозных значений. Формулы выведены алгебраическим путем.

Рисунок 47 – Программа. Нахождение значения переменных для нашего массива.
Далее находим коэфициент детерминированности, сравниваем каждый элемент массива x для нахождения наибольшего, сравниваем каждый элемент массива x для нахождения наименьшего, вычисляем прогнозное значение x и прогнозное значение y.

Рисунок 48 – Нахождение искомых данных, используя значения переменных.
После ввода количества элементов массива, программа выдает искомые данные.

Рисунок 48 – Результат использования программы.
Заключение
Таким образом, исходными данными являются два одномерных массива одинаковой длины, содержащие эмпирические данные. Между величинами x и y существует некоторая функциональная зависимость, но ее аналитический вид неизвестен, следовательно, нужно найти эмпирическую формулу. Нахождение аналитической зависимости между эмпирическими величинами называется аппроксимацией функции, заданной таблично. Чаще всего для аппроксимации используют метод наименьших квадратов (МНК). Построение эмпирических формул состоит из двух этапов
1. Выяснение общего вида этой формулы
2. Определение ее наилучших параметров.
Исследована эмпирическая зависимость содержания ионов Cl– от плотности воды, поступающей в скважину вместе с нефтью