Добавлен: 30.11.2023
Просмотров: 102
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2. Задача. Исследование зависимости содержания ионов от плотности пластовой воды
2.4 Вычисление прогнозного значения
3. Расчеты для определения коэффициентов зависимости и
3.1 Расчеты для "общего" уравнения
3.2 Расчеты для "специализированного" уравнения
3.3 Вычисление прогнозного значения
4.3 Вычисление прогнозного значения
5. Расчеты для определения коэффициентов зависимости и
5.1 Расчеты для "общего" уравнения
, для этого отнимем от единицы отношение суммы остатка деленную на сумму полную.
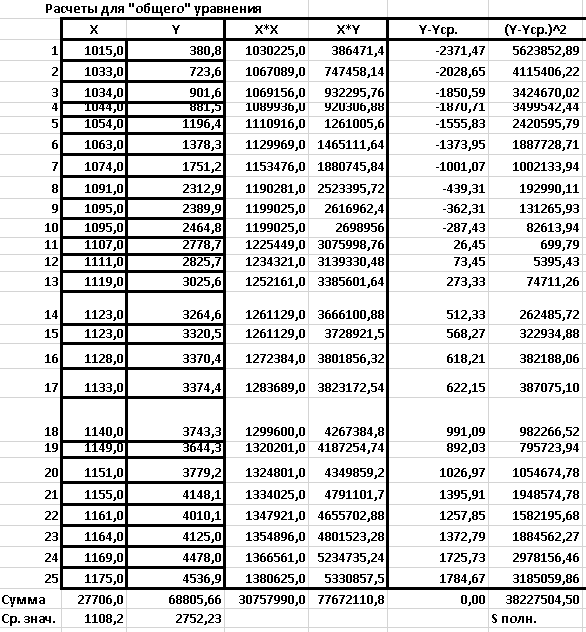
Рисунок 9 - Расчеты для уравнения общего вида. Нахождение коэффициентов.
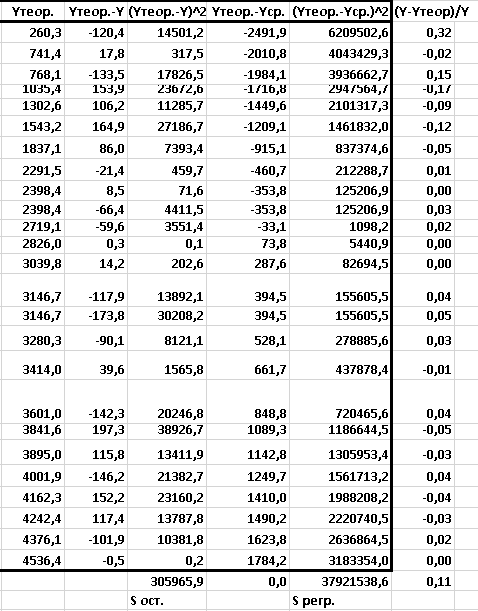
Рисунок 10 - Расчеты для уравнения общего вида. Решение матрицы. Нахождение коэффициентов.
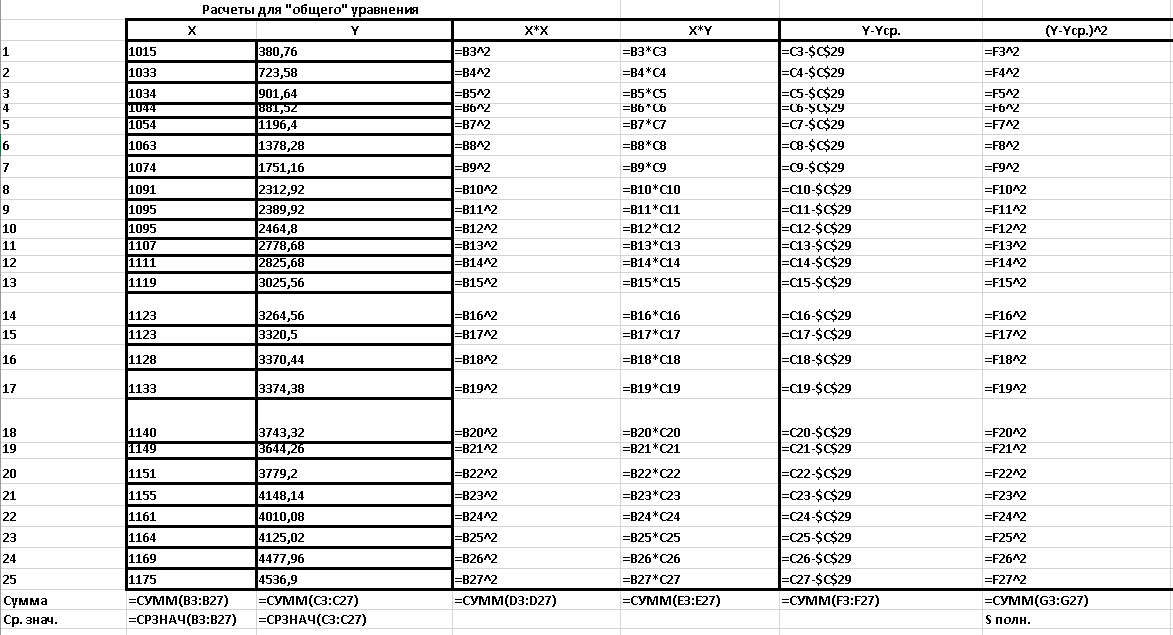
Рисунок 11 - Расчеты для уравнения общего вида. Нахождение коэффициентов. Режим отображения формул.
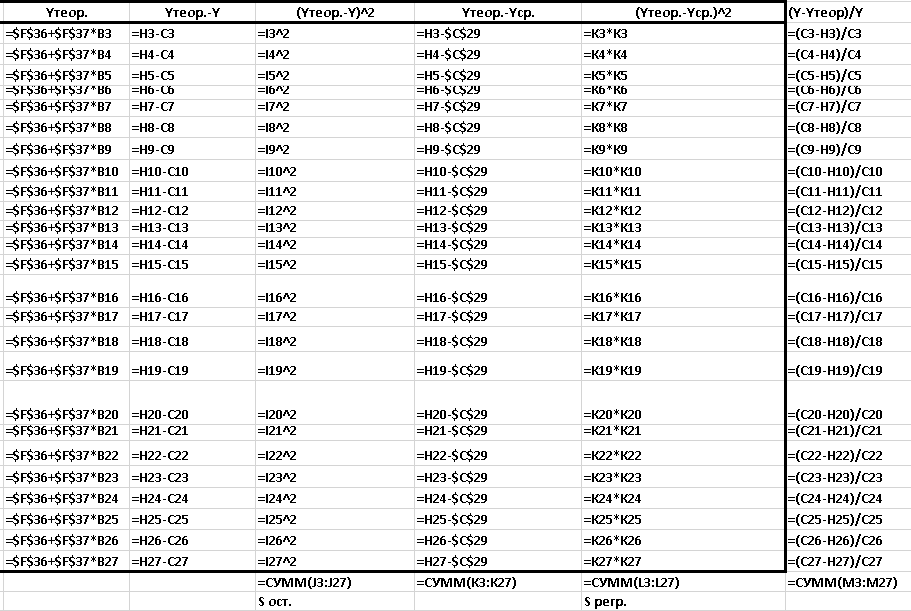
Рисунок 12 - Расчеты для уравнения общего вида. Нахождение коэффициентов. Режим отображения формул.
Рисунок 13 - Решение матрицы.
Рисунок 14 - Решение матрицы. Режим отображения формул.
Для первого графика (с помощью вставка - точечная диаграмма) выбираем значения X и Y. Обозначаем оси, выбираем линию тренда. В работе с диаграммами - конструктор, выбираем формат линии тренда. Ставим галочки на нужные пункты (рис 8), выбираем цвет и тип линий. Программа автоматически выдаст коэффициент уравнение функции.
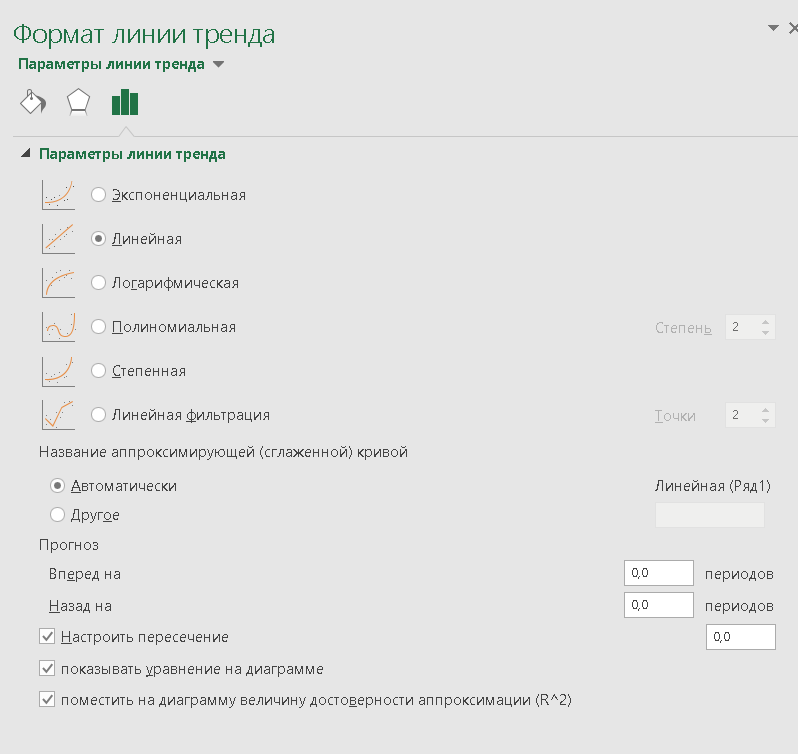
Рисунок 15- Настройка параметров линии тренда.
Те же действия производим со значениями Z и Y
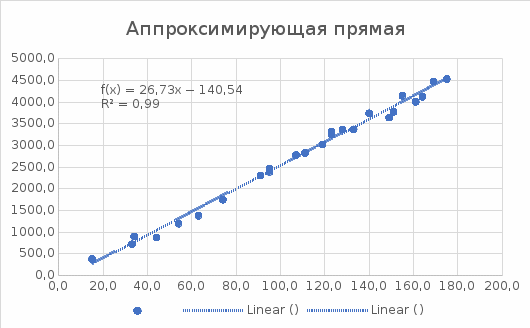
Рисунок 16 - Готовый график исследования.
Находим X прогнозное. Для этого при помощи функции максимального значения от X и дальнейшего его произведения на разницу максимального и минимального значения X находим нужное выражение.
Записываем значения коэффициентов из специализированного уравнения и общего. Для этого находим Y прогнозное для специализированного уравнения: коэффициент с умножаем на разность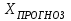 . -1000. И общего :
. -1000. И общего : умножаем на
умножаем на 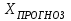 и добавляем
и добавляем  .Вычисляем разницу абсолютную, для этого от
.Вычисляем разницу абсолютную, для этого от 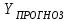 общего отнимаем
общего отнимаем 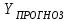 специализированное. После чего относительную разницу делим на
специализированное. После чего относительную разницу делим на 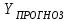 и получаем разницу абсолютную.
и получаем разницу абсолютную.
Рисунок 17 – Вычисление прогнозных значений и разницы - абсолютной и относительной.

Рисунок 18 – Вычисление прогнозных значений и разницы - абсолютной и относительной. Режим отображения формул
Для ввода данных используется команда ►Вставка► Компонента из главного меню MathCAD. Будет запущен Мастер (специальная программа), который обеспечит выполнение всей процедуры ввода, результат ввода будет находиться в двумерном массиве W. Далее эти данные (по столбцам) присваиваем одномерным массивам X и Y, с которыми выполняем все дальнейшие операции.
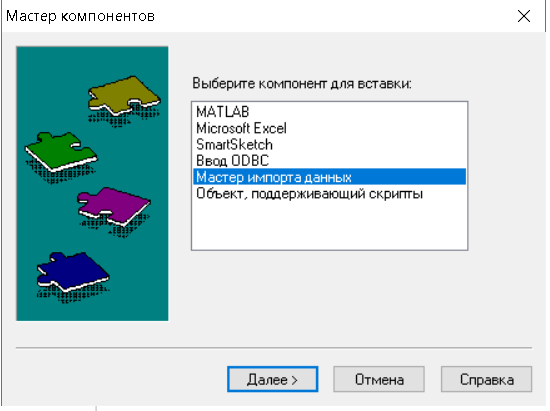
Рисунок 19 - Решение задачи. Подготовка данных и запуск Мастера Компонентов для ввода данных в системе MathCAD.
Определяем начальный индекс с помощью ORIGIN. Вбиваем количество наблюдений используя rows. Устанавливаем пределы изменения индекса векторов: присваиваем значения от 1 до N (количество наблюдений). Эмпирические данные раскладываем по отдельным “векторам”- массивам X и Y. Выводим исходные данные, образуются два массива X и Y.
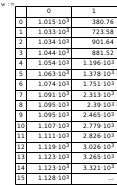
Рисунок 20 - Создание двумерного массива.
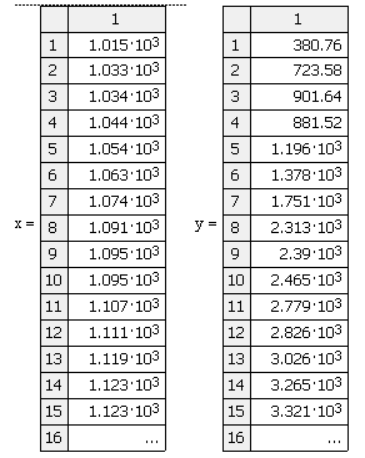
Рисунок 21 - Операции с массивом W.
Вычисляем некоторые характеристики эмпирических данных:


Рисунок 9 - Расчеты для уравнения общего вида. Нахождение коэффициентов.

Рисунок 10 - Расчеты для уравнения общего вида. Решение матрицы. Нахождение коэффициентов.

Рисунок 11 - Расчеты для уравнения общего вида. Нахождение коэффициентов. Режим отображения формул.

Рисунок 12 - Расчеты для уравнения общего вида. Нахождение коэффициентов. Режим отображения формул.
| А | | | В | |
| 25 | 27706,0 | | 68805,66 | |
| 27706,0 | 30757990,0 | | 77672110,8 | |
| | | | | |
| А^(-1) | | | | |
| 23,17311 | -0,020873734 | | а1= | -26866,06237 |
| -0,02087 | 1,8835E-05 | | а2= | 26,72551863 |
Рисунок 13 - Решение матрицы.
| А | | | В | |
| =A27 | =B28 | | =C28 | |
| =B28 | =D28 | | =E28 | |
| | | | | |
| А^(-1) | | | | |
| =МОБР(B32:C33)__=МОБР(B32:C33)'>=МОБР(B32:C33) | =МОБР(B32:C33) | | а1= | =МУМНОЖ(B36:C37;E32:E33) |
| =МОБР(B32:C33) | =МОБР(B32:C33) | | а2= | =МУМНОЖ(B36:C37;E32:E33) |
Рисунок 14 - Решение матрицы. Режим отображения формул.
2.3. Произведение расчетов с помощью графика и линии тренда таблично заданной функции средствами табличного процессора Microsoft Excel
Для первого графика (с помощью вставка - точечная диаграмма) выбираем значения X и Y. Обозначаем оси, выбираем линию тренда. В работе с диаграммами - конструктор, выбираем формат линии тренда. Ставим галочки на нужные пункты (рис 8), выбираем цвет и тип линий. Программа автоматически выдаст коэффициент уравнение функции.

Рисунок 15- Настройка параметров линии тренда.
Те же действия производим со значениями Z и Y

Рисунок 16 - Готовый график исследования.
2.4 Вычисление прогнозного значения
Находим X прогнозное. Для этого при помощи функции максимального значения от X и дальнейшего его произведения на разницу максимального и минимального значения X находим нужное выражение.
Записываем значения коэффициентов из специализированного уравнения и общего. Для этого находим Y прогнозное для специализированного уравнения: коэффициент с умножаем на разность
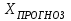 . -1000. И общего :
. -1000. И общего : умножаем на
умножаем на 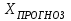 и добавляем
и добавляем  .Вычисляем разницу абсолютную, для этого от
.Вычисляем разницу абсолютную, для этого от 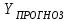 общего отнимаем
общего отнимаем 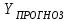 специализированное. После чего относительную разницу делим на
специализированное. После чего относительную разницу делим на 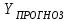 и получаем разницу абсолютную.
и получаем разницу абсолютную.| Вычисление прогнозного значения | | | | | |
| | x_прогноз | 1159 | | | |
| | | | | | |
| | Коэффицент | | | Разница | |
| | а1 | а2 или с | y_прогноз | абсолютная | относительная, % |
| специализированное | | 25,63 | 4074,59 | 34,23 | 0,84% |
| общее | -26866,0624 | 26,7255 | 4108,81 | | |
Рисунок 17 – Вычисление прогнозных значений и разницы - абсолютной и относительной.

Рисунок 18 – Вычисление прогнозных значений и разницы - абсолютной и относительной. Режим отображения формул
3. Расчеты для определения коэффициентов зависимости и
с использованием MathCAD
Для ввода данных используется команда ►Вставка► Компонента из главного меню MathCAD. Будет запущен Мастер (специальная программа), который обеспечит выполнение всей процедуры ввода, результат ввода будет находиться в двумерном массиве W. Далее эти данные (по столбцам) присваиваем одномерным массивам X и Y, с которыми выполняем все дальнейшие операции.

Рисунок 19 - Решение задачи. Подготовка данных и запуск Мастера Компонентов для ввода данных в системе MathCAD.
Определяем начальный индекс с помощью ORIGIN. Вбиваем количество наблюдений используя rows. Устанавливаем пределы изменения индекса векторов: присваиваем значения от 1 до N (количество наблюдений). Эмпирические данные раскладываем по отдельным “векторам”- массивам X и Y. Выводим исходные данные, образуются два массива X и Y.

Рисунок 20 - Создание двумерного массива.

Рисунок 21 - Операции с массивом W.
Вычисляем некоторые характеристики эмпирических данных:
-
Вычисляем с помощью функции mean
с помощью функции mean -
Вычисляем сумму всех значений равных Y-
-
Находим минимальное и максимальное значение X помощью функции min и max -
Устанавливаем размах величины X, равный разности максимального и минимального значений X. -
Вычисляем прогнозное значение X ,при значении которого в дальнейших действиях вычислим . Для этого вычислим произведение X максимального на размах X.
. Для этого вычислим произведение X максимального на размах X. -
Находим коэффициент корреляции между величинами X и Y используя функцию corr(X,Y).
