Файл: Курсовая работа по дисциплине Цифровые системы управления в мехатронике АлФахри Ф. Ф. А. М.docx
Добавлен: 03.12.2023
Просмотров: 107
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
; коэффициент трансформации 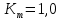 ; частота вращения
; частота вращения 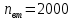 об/мин.
об/мин.
Максимальный угол поворота исполнительного вала электропривода:
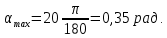
Коэффициент передачи вращающегося трансформатора:
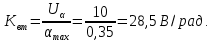
Определяем установившуюся ошибку относительно задающего воздействия по формуле:
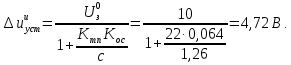
Определяем установившуюся ошибку относительно момента сопротивления по формуле:
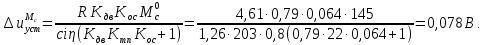
Определяем суммарную установившуюся ошибку электропривода с двигателем типа 2ПН90LYXL4:
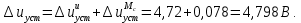
2.2. Моделирование нескорректированного замкнутого контура скорости с двигателем типа 2ПН90LYXL4. Оценка качества переходных процессов. Определение установившиеся ошибки относительно задающего воздействия и момента сопротивления.
ССДМ ЭП в среде MatLab представлена на рис. 2.2.1.
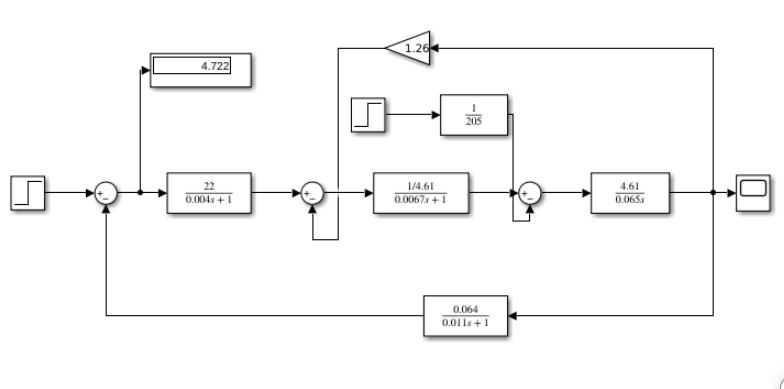
Рис. 2.2.1. ССДМ нескорректированного контура скорости
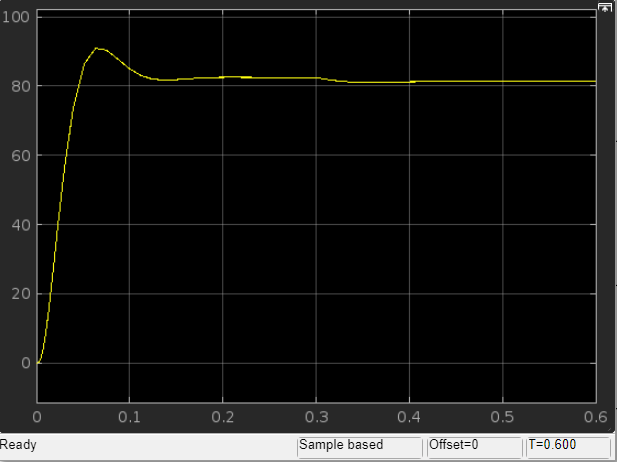
На рис. 2.2.2 представлена зависимость угловой скорости от времени нескорректированного контура скорости. Наброс момента производился через 0,5 с после пуска системы «преобразователь – двигатель».
производился через 0,5 с после пуска системы «преобразователь – двигатель».
Из графика видно, что установившееся значение скорости двигателя без нагрузки составляет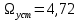 рад/с. За счет влияния
рад/с. За счет влияния  угловая скорость уменьшилась примерно на 3,4 рад/c.
угловая скорость уменьшилась примерно на 3,4 рад/c.
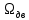 , рад/с
, рад/с
 t, c
t, c
Рис. 2.2.2. Зависимость угловой скорости от времени нескорректированного контура скорости
График характеризует колебательную систему с перерегулированием около 16 % и числом колебаний N = 1 и. Время протекания переходного процесса составляет 0,4 с. Наличие колебаний обусловлено комплексно-сопряженными корнями характеристического уравнения замкнутой системы.
Установившиеся ошибки по задающему воздействию и по моменту сопротивления, которые составили:
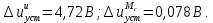
Таким образом, суммарная установившаяся ошибка электропривода с двигателем типа 2ПН90LYXL4:

Результаты моделирования подтверждают правильность расчетов, проведенных в примере 2.1а.
3. Оптимизация контура скорости
3.1. Расчёт параметров и электрической схемы аналогового ПИД-регулятора. Выбор RC-элементов и операционного усилителя.
Поскольку, 4Тэ меньше, чем Тм, то передаточную функцию регулятора скорости представим в виде:
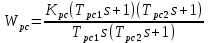
где постоянные времени
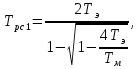
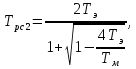
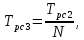
коэффициент передачи
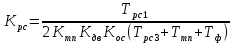
На основании схемы, представленной на рис. 3.9, постоянные времени и коэффициент передачи ПИД-регулятора скорости определяются по формулам:
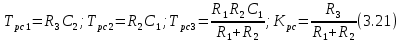
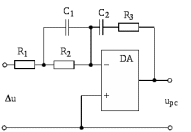
Рис. 3.9. Электрическая схема ПИД-регулятора скорости
Заметим, что в формулах (3.21) число неизвестных превышает число уравнений. Поэтому в инженерной практике прибегают к способу, когда значении емкостей назначаются из стандартного ряда 1; 10; 22; 33; 47; 100 мкФ. Тогда порядок расчета сводится к следующему.
превышает число уравнений. Поэтому в инженерной практике прибегают к способу, когда значении емкостей назначаются из стандартного ряда 1; 10; 22; 33; 47; 100 мкФ. Тогда порядок расчета сводится к следующему.
Переходим к расчету номинальных значений RC-элементов.
Постоянные времени РС:
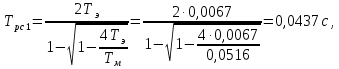
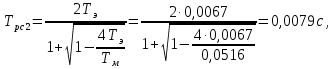
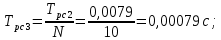
Коэффициент передачи регулятора скорости:
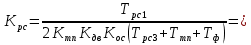
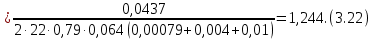
Задаем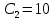 мкФ и по табл. П6 выбираем конденсатор Panasonic серии NHG. Тогда
мкФ и по табл. П6 выбираем конденсатор Panasonic серии NHG. Тогда
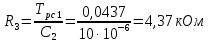
Приводим сопротивление к номинальному значению по ряду Е192 (см. табл. П5) и принимаем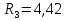 кОм.
кОм.
Задаем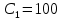 мкФ и по табл. П6 выбираем конденсатор Panasonic серии NHG. Тогда
мкФ и по табл. П6 выбираем конденсатор Panasonic серии NHG. Тогда
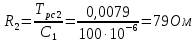
Приводим сопротивление к номинальному значению по ряду Е192 (см. табл. П5) и принимаем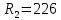 Ом.
Ом.
Рассчитываем сопротивление:
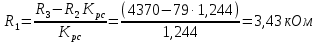
Приводим сопротивление к номинальному значению по ряду Е192 (см. табл. П5) и принимаем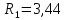 4 кОм.
4 кОм.
По полученным номинальным значениям сопротивлений РС пересчитываем коэффициент передачи
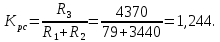
Полученное значение не отличается от величины коэффициента передачи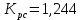 , поэтому подстройки резистора
, поэтому подстройки резистора 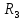 не требуется.
не требуется.
3.2. Проведение моделирования КС с аналоговым ПИД-регулятором скорости. Получение графиков переходных функций по задающему воздействию и по моменту сопротивления нагрузки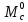 . Построение графиков ЛЧХ разомкнутого КС. Проведение анализа результатов моделирования.
. Построение графиков ЛЧХ разомкнутого КС. Проведение анализа результатов моделирования.
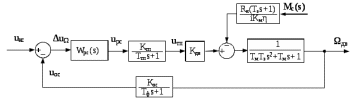
Для моделирования построим ССДМ КС в системе Simulink, представленную на рис. 3.10.
Рис. 3.10. Структурная схема динамической модели контура скорости
в системе Simulink
В блоке Step задаём воздействие, равное входному напряжению суммирующего усилителя КС В, а в блоке Step 1 значение момента сопротивления нагрузки
В, а в блоке Step 1 значение момента сопротивления нагрузки  . На рис. 3.11 изображен график переходной характеристики контура скорости по управляющему воздействию.
. На рис. 3.11 изображен график переходной характеристики контура скорости по управляющему воздействию.
Для построения переходной характеристики по моменту сопротивления нагрузки Мс устанавливаем соответственно в блоке Step входное воздействие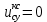 В, а в блоке Step 1 – момент сопротивления
В, а в блоке Step 1 – момент сопротивления 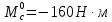 .. Полученная зависимость представлена на рис. 3.12.
.. Полученная зависимость представлена на рис. 3.12.
Ω(t), рад/с
 t,c
t,c
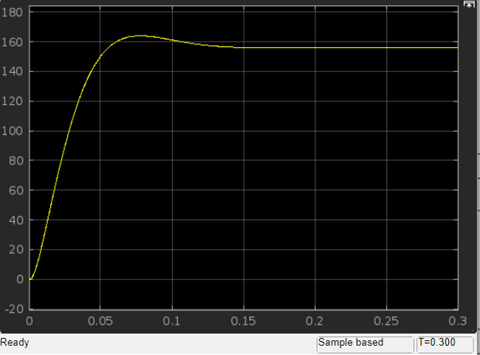
Рис. 3.11. График зависимости угловой скорости от времени скорректированного контура скорости по сигналу задания
Ω(t), рад/с
 t, c
t, c
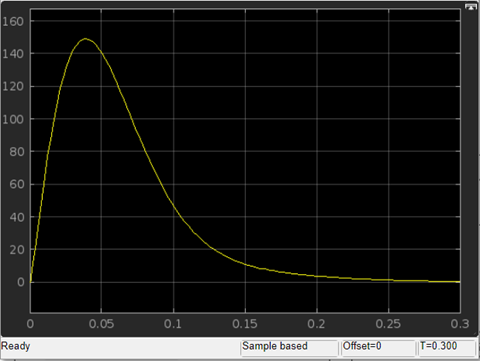
Рис. 3.12. График зависимости угловой скорости от времени скорректированного контура скорости по моменту сопротивления
Переходим к анализу полученных графиков. По графику на рис. 3.11 определяем перерегулирование:
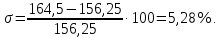
Перерегулирование, полученное в результате моделирования, отличается от требуемого значения 4,3 %. Такое изменение обусловлено влиянием малой постоянной времени Тф. Если принять Тф = 0, то перерегулирование будет равно 4,3 %, а передаточная функция ТГ представится безынерционным звеном:
Wос(s) = Кос.
При этом суммарную малую постоянную времени КС следует рассчитывать по формуле:
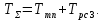
Время нарастания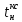 определяется в первой точке пересечения графика переходной функции и установившегося значения угловой скорости Ωуст и составляет:
определяется в первой точке пересечения графика переходной функции и установившегося значения угловой скорости Ωуст и составляет:
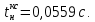
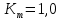 ; частота вращения
; частота вращения 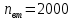 об/мин.
об/мин.Максимальный угол поворота исполнительного вала электропривода:
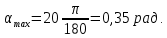
Коэффициент передачи вращающегося трансформатора:
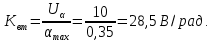
2. Исследование нескорректированного контура скорости
2.1. Определение суммарной установившейся ошибки электропривода с двигателем типа 2ПН90LYXL4.
Определяем установившуюся ошибку относительно задающего воздействия по формуле:
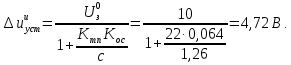
Определяем установившуюся ошибку относительно момента сопротивления по формуле:
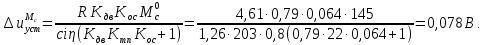
Определяем суммарную установившуюся ошибку электропривода с двигателем типа 2ПН90LYXL4:
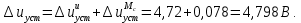
2.2. Моделирование нескорректированного замкнутого контура скорости с двигателем типа 2ПН90LYXL4. Оценка качества переходных процессов. Определение установившиеся ошибки относительно задающего воздействия и момента сопротивления.
ССДМ ЭП в среде MatLab представлена на рис. 2.2.1.

Рис. 2.2.1. ССДМ нескорректированного контура скорости
На рис. 2.2.2 представлена зависимость угловой скорости от времени нескорректированного контура скорости. Наброс момента
 производился через 0,5 с после пуска системы «преобразователь – двигатель».
производился через 0,5 с после пуска системы «преобразователь – двигатель». Из графика видно, что установившееся значение скорости двигателя без нагрузки составляет
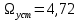 рад/с. За счет влияния
рад/с. За счет влияния 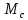 угловая скорость уменьшилась примерно на 3,4 рад/c.
угловая скорость уменьшилась примерно на 3,4 рад/c.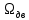 , рад/с
, рад/с t, c
t, cРис. 2.2.2. Зависимость угловой скорости от времени нескорректированного контура скорости
График характеризует колебательную систему с перерегулированием около 16 % и числом колебаний N = 1 и. Время протекания переходного процесса составляет 0,4 с. Наличие колебаний обусловлено комплексно-сопряженными корнями характеристического уравнения замкнутой системы.
Установившиеся ошибки по задающему воздействию и по моменту сопротивления, которые составили:
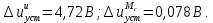
Таким образом, суммарная установившаяся ошибка электропривода с двигателем типа 2ПН90LYXL4:

Результаты моделирования подтверждают правильность расчетов, проведенных в примере 2.1а.
3. Оптимизация контура скорости
3.1. Расчёт параметров и электрической схемы аналогового ПИД-регулятора. Выбор RC-элементов и операционного усилителя.

Поскольку, 4Тэ меньше, чем Тм, то передаточную функцию регулятора скорости представим в виде:
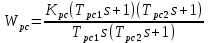
где постоянные времени
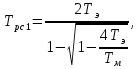
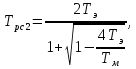
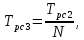
коэффициент передачи
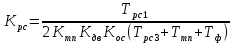
На основании схемы, представленной на рис. 3.9, постоянные времени и коэффициент передачи ПИД-регулятора скорости определяются по формулам:
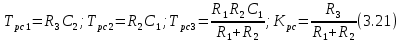

Рис. 3.9. Электрическая схема ПИД-регулятора скорости
Заметим, что в формулах (3.21) число неизвестных
 превышает число уравнений. Поэтому в инженерной практике прибегают к способу, когда значении емкостей назначаются из стандартного ряда 1; 10; 22; 33; 47; 100 мкФ. Тогда порядок расчета сводится к следующему.
превышает число уравнений. Поэтому в инженерной практике прибегают к способу, когда значении емкостей назначаются из стандартного ряда 1; 10; 22; 33; 47; 100 мкФ. Тогда порядок расчета сводится к следующему.-
Задаемся емкостью и рассчитываем
и рассчитываем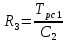 .
. -
Задаемся емкостью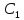 и рассчитываем
и рассчитываем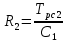 .
. -
Согласно формуле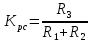 сопротивление
сопротивление 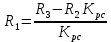 .
.
Переходим к расчету номинальных значений RC-элементов.
Постоянные времени РС:
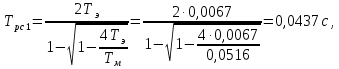
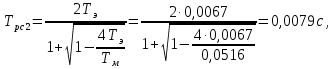
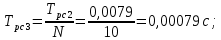
Коэффициент передачи регулятора скорости:
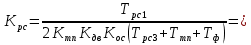
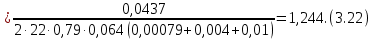
Задаем
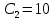 мкФ и по табл. П6 выбираем конденсатор Panasonic серии NHG. Тогда
мкФ и по табл. П6 выбираем конденсатор Panasonic серии NHG. Тогда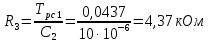
Приводим сопротивление к номинальному значению по ряду Е192 (см. табл. П5) и принимаем
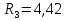 кОм.
кОм.Задаем
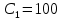 мкФ и по табл. П6 выбираем конденсатор Panasonic серии NHG. Тогда
мкФ и по табл. П6 выбираем конденсатор Panasonic серии NHG. Тогда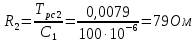
Приводим сопротивление к номинальному значению по ряду Е192 (см. табл. П5) и принимаем
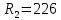 Ом.
Ом.Рассчитываем сопротивление:
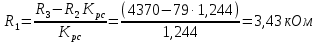
Приводим сопротивление к номинальному значению по ряду Е192 (см. табл. П5) и принимаем
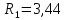 4 кОм.
4 кОм.По полученным номинальным значениям сопротивлений РС пересчитываем коэффициент передачи
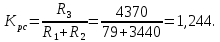
Полученное значение не отличается от величины коэффициента передачи
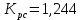 , поэтому подстройки резистора
, поэтому подстройки резистора 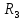 не требуется.
не требуется.3.2. Проведение моделирования КС с аналоговым ПИД-регулятором скорости. Получение графиков переходных функций по задающему воздействию и по моменту сопротивления нагрузки
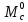 . Построение графиков ЛЧХ разомкнутого КС. Проведение анализа результатов моделирования.
. Построение графиков ЛЧХ разомкнутого КС. Проведение анализа результатов моделирования. Для моделирования построим ССДМ КС в системе Simulink, представленную на рис. 3.10.

Рис. 3.10. Структурная схема динамической модели контура скорости
в системе Simulink
В блоке Step задаём воздействие, равное входному напряжению суммирующего усилителя КС
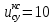 В, а в блоке Step 1 значение момента сопротивления нагрузки
В, а в блоке Step 1 значение момента сопротивления нагрузки 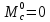 . На рис. 3.11 изображен график переходной характеристики контура скорости по управляющему воздействию.
. На рис. 3.11 изображен график переходной характеристики контура скорости по управляющему воздействию.Для построения переходной характеристики по моменту сопротивления нагрузки Мс устанавливаем соответственно в блоке Step входное воздействие
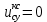 В, а в блоке Step 1 – момент сопротивления
В, а в блоке Step 1 – момент сопротивления 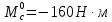 .. Полученная зависимость представлена на рис. 3.12.
.. Полученная зависимость представлена на рис. 3.12. Ω(t), рад/с
 t,c
t,cРис. 3.11. График зависимости угловой скорости от времени скорректированного контура скорости по сигналу задания
Ω(t), рад/с
 t, c
t, cРис. 3.12. График зависимости угловой скорости от времени скорректированного контура скорости по моменту сопротивления
Переходим к анализу полученных графиков. По графику на рис. 3.11 определяем перерегулирование:
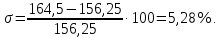
Перерегулирование, полученное в результате моделирования, отличается от требуемого значения 4,3 %. Такое изменение обусловлено влиянием малой постоянной времени Тф. Если принять Тф = 0, то перерегулирование будет равно 4,3 %, а передаточная функция ТГ представится безынерционным звеном:
Wос(s) = Кос.
При этом суммарную малую постоянную времени КС следует рассчитывать по формуле:
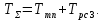
Время нарастания
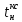 определяется в первой точке пересечения графика переходной функции и установившегося значения угловой скорости Ωуст и составляет:
определяется в первой точке пересечения графика переходной функции и установившегося значения угловой скорости Ωуст и составляет: