Файл: Курсовая работа по дисциплине Цифровые системы управления в мехатронике АлФахри Ф. Ф. А. М.docx

Проверяем соответствие полученного значения требованиям настройки на ОМ:



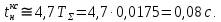
Из анализа графика на рис. 3.12 следует, что при воздействии неизменного по величине момента сопротивления М_с моментная составляющая ошибки ΔΩ_м примерно через 0,4 с становится равной нулю. Это говорит о том, что искусственная механическая характеристика стала абсолютно жёсткой. Увеличение точности обусловлено наличием в структуре регулятора скорости интегральной составляющей.

Далее переходим к построению ЛЧХ:

num1=[0.0004 0.064 1.244];

den1=[0.000034 0.0437 0];

sys1=tf(num1,den1)

num2=[22];

den2=[0.004 1];

sys2=tf(num2,den2)

num3=[0.79];[

den3=[0.00034 0.0516 1];

sys3=tf(num3,den3)

num4=[0.064];

den4=[0.011 1];

sys4=tf(num4,den4)

sys5=sys1*sys2*sys3*sys4

sys5 =

0.0004449 s^2 + 0.07119 s + 1.384
---------------------------------------------------------------------------------------
5.086e-13 s^6 + 9.043e-10 s^5 + 3.615e-07 s^4 + 5.287e-05 s^3 + 0.002944 s^2 + 0.0437 s
num = [0.0004449 0.07119 1.384];

den = [5.086e-13 9.043e-10 3.615e-07 5.287e-05 0.002944 0.0437 0];

bode(num, den)

Результаты моделирования представлены на рис. 3.12.

Из анализа графиков видно, что запасы устойчивости по фазе и амплитуде составляют L_з = 16,8 дБ (Gain Margin) и 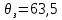(Phase Margin) соответственно.

Значение фазы 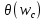соответствует частоте среза ω_с, т. е. точке пересечения графика ЛАЧХ с линией 0 дБ.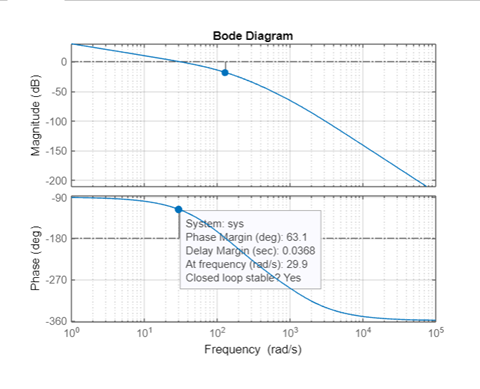



Рис. 3.12. Логарифмические частотные характеристики контура скорости

Вывод: результаты моделирования подтверждают правильность расчёта параметров РС и позволяют сделать вывод о том, что КС настроен на ОМ.

5. Синтез аналогового регулятора положения (графоаналитический метод)

5.1. Синтез регулятора положения в системе с астатизмом второго порядка

• 
  максимальная угловая скорость нагрузки Ω_max = 44 град/с;
  
• 
  максимальное угловое ускорение нагрузки ε_max = 11 град/с²;
  
• 
  яшибка по скорости _ = 25 мин;
  
• 
  ошибка по ускорению _ = 50 мин
  
• 
  передаточное число редуктора i₁ = 203;
  
• 
  показатель колебательности М = 1,4;
  
• 
  коэффициент передачи вращающегося трансформатора K_вт = 28,5В/рад.
  
• 
  Моментная составляющая ошибки .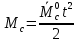
  

---

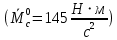Определяем параметры желаемой передаточной функции ЭП. Коэффициент передачи по ускорению будет равен:

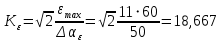с^{– 2}.

Значение базовой частоты определится по формуле:

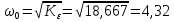с^{– 1}.

По выражениям рассчитываем постоянные времени:

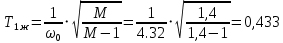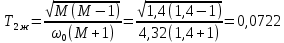с;

с.

С учётом проведённых расчётов запишем желаемую передаточную функцию ЭП с астатизмом второго порядка:

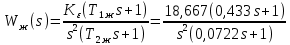. (5.13)

Передаточная функция неизменяемой части:

.

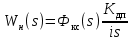Данные для определения передаточной функции 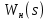примем по примеру 3.2 и составим программу:

num1=[0.0004 0.064 1.244];

den1=[0.000034 0.0437 0];

sys1=tf(num1,den1)

num2=[22];

den2=[0.004 1];

sys2=tf(num2,den2)

num3=[0.79];

den3=[0.00034 0.0516 1];

sys3=tf(num3,den3)

sys4=sys1*sys2*sys3;

num5=[0.064];

den5=[0.01 1];

sys5=tf(num5,den5);

sys6=feedback(sys4,sys5);

num7=[28.5];

den7=[203.4 0];

sys7=tf(num7,den7);

sys8=sys6*sys7

sys8 =


0.001981 s^3 + 0.5151 s^2 + 37.86 s + 616.2
------------------------------------------------------------
9.405e-11 s^7 + 1.681e-07 s^6 + 6.828e-05 s^5 + 0.01025 s^4 + 0.6805 s^3 + 23.37 s^2 + 281.4 s

В приведенной программе оператор feedback осуществляет операцию замыкания отрицательной обратной связи контура скорости согласно уравнению:

.

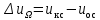Для определения передаточной функции регулятора положения составляем следующую программу:

num1=[18.667*0.433 18.667];

den1=[0.0722 1 0 0];

sys1=tf(num1, den1);

num2=[0.001981 0.5151 37.86 616.2];

den2=[9.405e-11 1.681e-07 6.828e-05 0.01025 0.6805 23.37 281.4 0];

sys2=tf(num2, den2);

sys3=sys1/sys2


sys3 =
7.602e-10 s^8 + 1.36e-06 s^7 + 0.000555 s^6 + 0.08412 s^5 + 5.692 s^4

+ 201.6 s^3 + 2711 s^2 + 5253 s

------------------------------------------------------------------------------

0.000143 s^6 + 0.03917 s^5 + 3.249 s^4 + 82.35 s^3 + 616.2 s^2


Составляем программу для определения ЛАЧХ регулятора положения, изображенную на рис. 5.2:

num=[7.602e-10 1.36e-06 0.000555 0.08412 5.692 201.6 2711 5253 0];

den=[0.000143 0.03917 3.249 82.35 616.2 0 0];

bode(num, den)



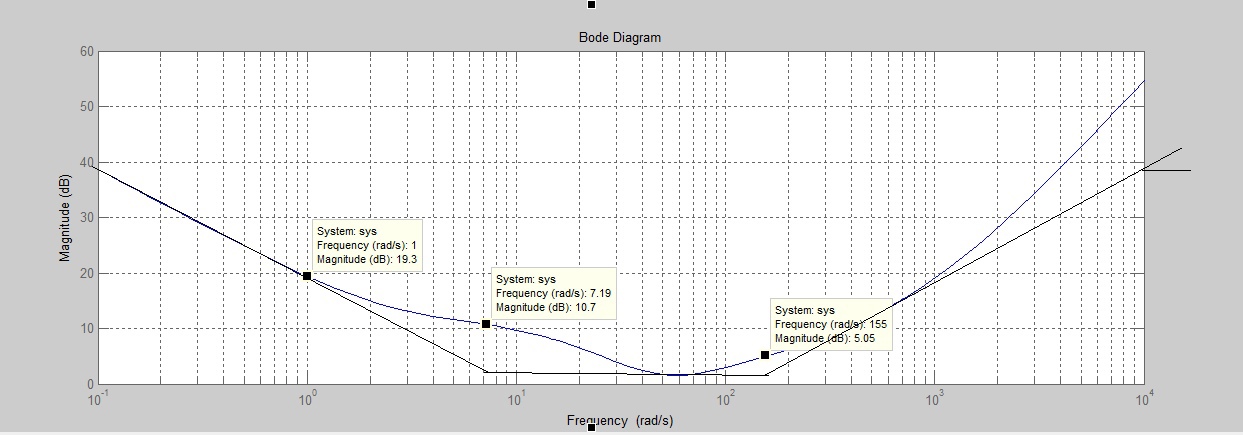
Рис. 5.2. ЛАЧХ регулятора положения

---

Переходим к анализу полученного графика. Низкочастотный участок ЛАЧХ регулятора положения проходит под наклоном –20 дБ/дек, постепенно изменяя наклон к среднечастотному участку до 0 дБ/дек. Высокочастотный участок полученной ЛАЧХ (  100 с^{– 1}) аппроксимируем двумя асимптотами с наклоном 20 дБ/дек и 0 дБ/дек.

Таким образом, проведённый анализ показывает, что ЛАЧХ следует аппроксимировать четырьмя асимптотами и придать регулятору положения свойства ПИД-регулятора.

Рассчитаем параметры передаточной функции регулятора положения. На частоте  = 1 находим:

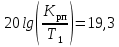дБ,

откуда 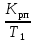= 9,2257 с^{– 1}.

По графику, представленному на рис. 5.2, определяем частоты сопряжения ₁ = 7,19 с^{– 1}; ₂ = 155 с^{– 1}; ₃ = 10000 с^{– 1} и рассчитываем постоянные времени:

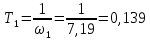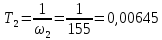с; 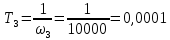с;

с.

Подставляя значение Т₁, получаем коэффициент передачи регулятора положения:

.

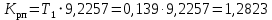С учётом полученных значений передаточная функция синтезированного регулятора положения принимает вид:

.

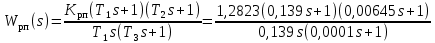Для построения динамической модели ЭП представим передаточную функцию РП (ПИД-регулятора) в виде произведения:

.

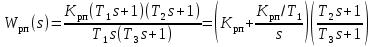Рис. 5.1.2. Структурная схема динамической модели электропривода в среде MatLab

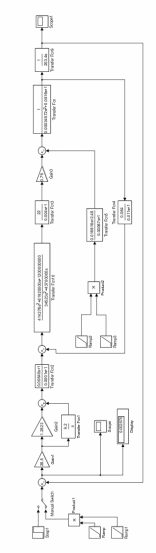
Результаты моделирования показаны на рис. 5.1.3-5.1.5.

α(t), рад

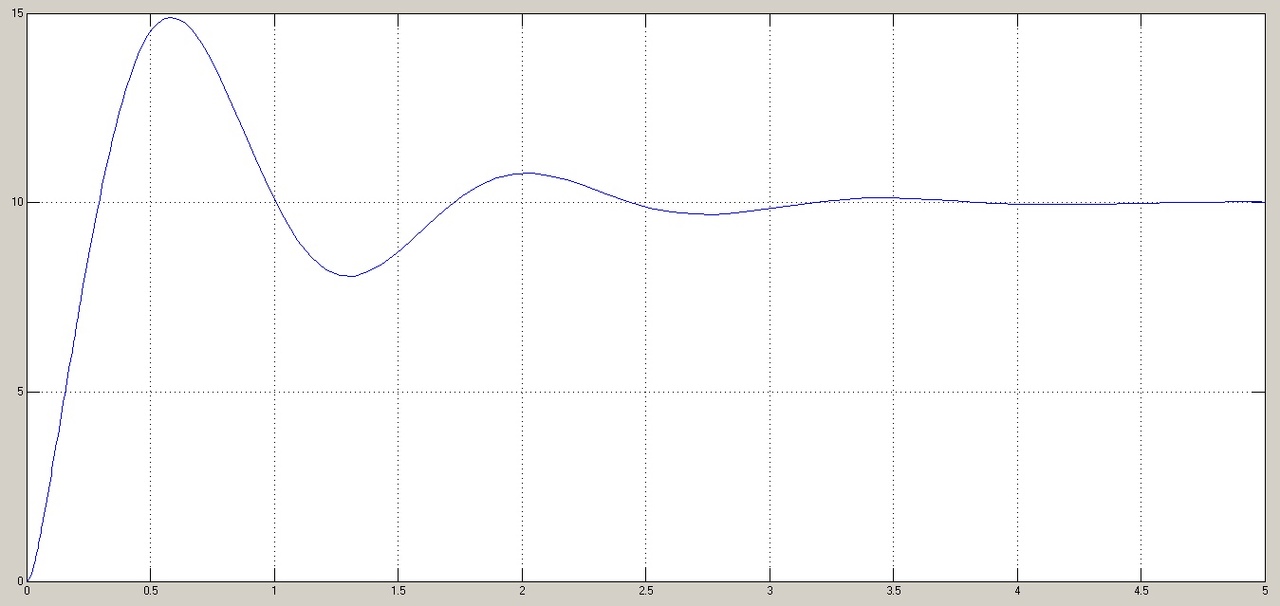t, c

Рис. 5.1.3. Переходная характеристика системы по задающему воздействию

, рад

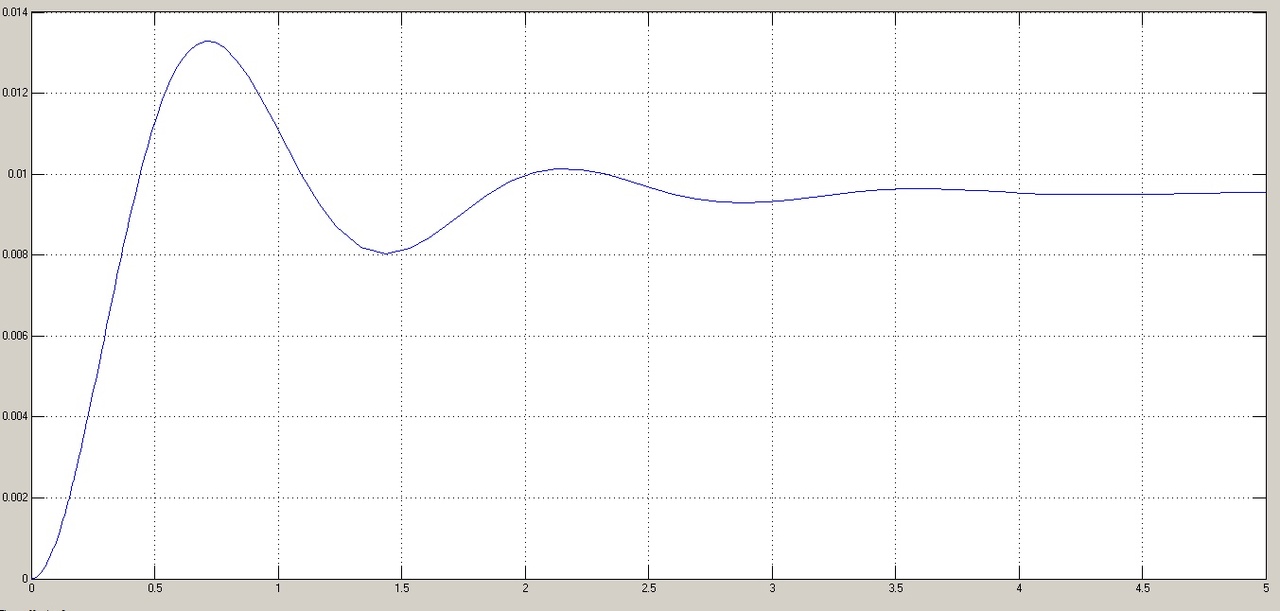t, c

Рис. 5.1.4. График ошибки системы при квадратично возрастающем

задающем воздействии

---

, рад

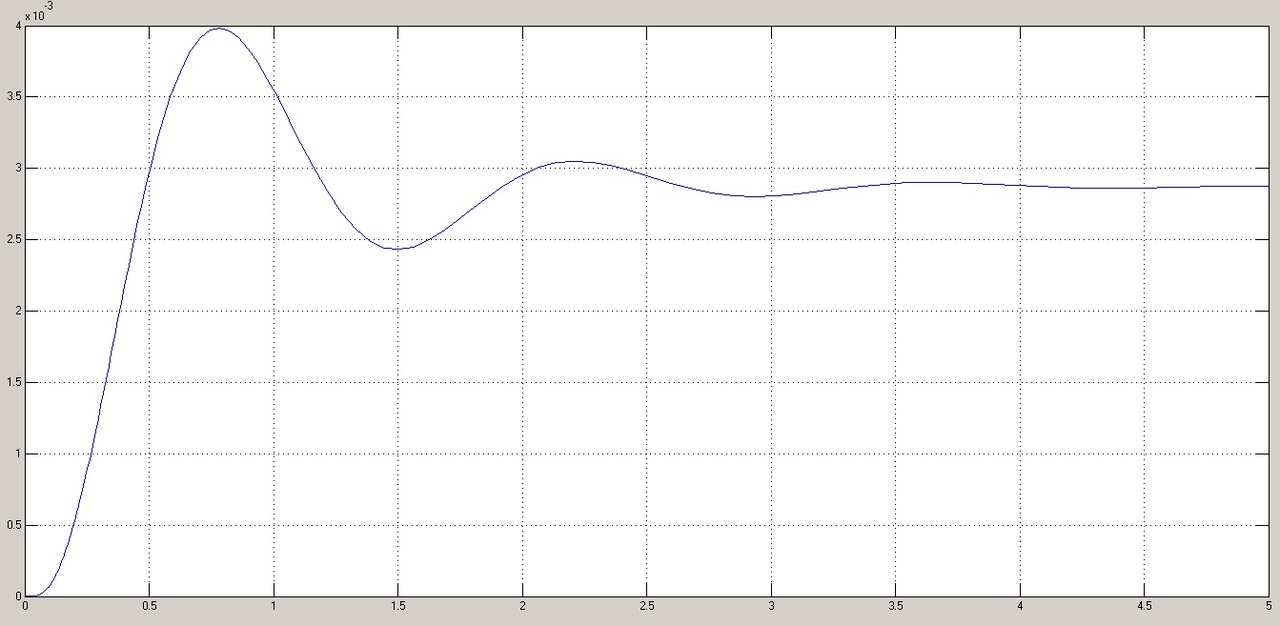t, c

Рис. 5.1.5. График моментной составляющей ошибки системы

при квадратично возрастающем моменте сопротивления

Анализ графика (рис. 5.1.3) показывает, что следящий позиционный ЭП отрабатывает ступенчатое воздействие 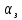примерно за 2,0 с с перерегулированием 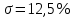и числом колебаний N < 1, что соответствует заданному показателю колебательности М = 1,1.

Поскольку контур положения содержит ПИД-регулятор положения, очевидно, что при ступенчатом и линейно возрастающем задающем воздействии статическая ошибка и ошибка по скорости будут равны нулю. На рис. 5.1.4 представлена характеристика при отработке типового задающего воздействия 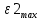/2. Установившаяся ошибка системы составляет примерно 25,44 мин. Моментная составляющая ошибки 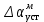при отработке квадратично возрастающего момента сопротивления 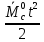составляет 3,3 мин по истечении 2,5 с (рис. 5.1.5).

---

5.2. Синтез регулятора положения в системе с астатизмом первого порядка

Определяем параметры желаемой передаточной функции ЭП.

Коэффициент передачи по скорости:

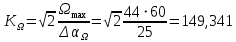с^{– 1}.

Коэффициент передачи по ускорению:

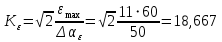с^{– 2}.

Значение базовой частоты будет равно:

с^{– 1}.

Рассчитываем постоянные времени:

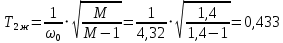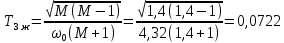с;

с.

Рассчитываем протяжённость среднечастотного участка желаемой ЛАЧХ:

.

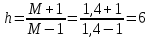Частоту, соответствующую максимальному запасу по фазе определяем по формуле:

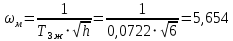с^{– 1}.

По условию обеспечения максимального запаса по фазе находим постоянную времени :

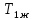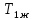 1/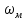 = 1/5,654 = 0,176 с.

Принимаем 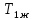= 2 с.

С учётом проведённых расчётов желаемая передаточная функция ЭП с астатизмом первого порядка запишется как:



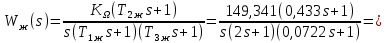
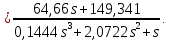
Составляем программу для определения передаточной функции регулятора положения ЭП с астатизмом первого порядка. Передаточную функцию неизменяемой части принимаем по примеру 5.1.

 num1=[64.66 149.341];

den1=[0.1444 2.0722 1 0];

sys1=tf(num1,den1);

num2=[0.001981 0.5151 37.86 616.2];

den2=[9.405e-11 1.681e-07 6.828e-05 0.01025 0.6805 23.37 281.4 0];

sys2=tf(num2,den2);

sys3=sys1/sys2

sys3 =

6.081e-09 s^8 + 1.088e-05 s^7 + 0.00444 s^6 + 0.673 s^5

+ 45.53 s^4 + 1613 s^3 + 2.169e04 s^2 + 4.202e04 s

------------------------------------------------------------------

0.0002861 s^6 + 0.07849 s^5 + 6.536 s^4 + 167.9 s^3 + 1315 s^2 + 616.2 s

Составляем программу для определения ЛАЧХ регулятора положения, изображенную на рис. 5.2.1:

num=[ 6.081e-09 1.088e-05 0.00444 0.673 45.53 1613 2.169e04 4.202e04 0];

den=[0.0002861 0.07849 6.536 167.9 1315 616.2 0];

---