Файл: Расчет электрических фильтров.docx

Порядок фильтра Чебышева находится также из рассмотрения (2.5) [1] , но при A = A_min и  =_з, т. е. ослабление рассматривается в полосе непропускания. А в ПН полином Чебышева Т_m() = chmarch, поэтому

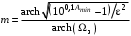(2.5)

Для вычисления функции archх рекомендуется соотношение:




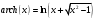
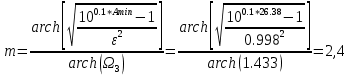
Необходимо взять m=3 порядок низкочастотного фильтра прототипа.

2.4. Расчёт передаточной функции НЧ – прототипа



Формируем нормированную передаточную функцию НЧ - прототипа в виде:



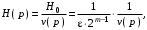
где v(р) – полином Гурвица, который можно записать через полюсы:





Производя вычисления, получим

3. 
   Пассивный LC – фильтр
   
   1. 
      3.1. Реализация схемы НЧ – прототипа
      

Для получения схемы НЧ - прототипа воспользуемся методом Дарлингтона, когда для двусторонне нагруженного фильтра (рис. 2.1) составляется выражение для входного сопротивления Z_вх.1(р) .



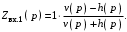
Для фильтров Чебышева третьего порядка сам полином Чебышева равен:



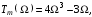
а полином h(р) будет:

---

Эта формула описывает входное сопротивление двухполюсника (согласно схеме на рис. 2.1 фильтр, нагруженный на сопротивление R_н, это действительно двухполюсник). А если известно выражение для входного сопротивления, то строим схему двухполюсника, воспользовавшись, методом Кауэра. По этому методу формула для Z_вх(р) разлагается в непрерывную дробь путем деления полинома числителя на полином знаменателя. При этом степень числителя должна быть больше степени знаменателя. Исходя из последнего, формула преобразуется к виду:



после чего производится ряд последовательных делений. Вначале числитель делим на знаменатель:



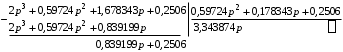
Затем первый делитель делим на первый остаток:



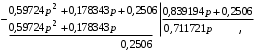
Второй делитель делим на второй остаток:



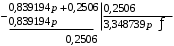
Третий делитель делим на третий остаток:



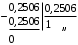
Получили четыре результата деления, которые отражают четыре нормированных по частоте и по сопротивлению элемента схемы в виде значений их проводимостей: pC, 1/pL, 1/R. Из анализа первого результата деления следует, что он отражает емкостную проводимость, поэтому все выражение (3.5) можно записать в виде цепной дроби:



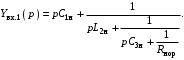
По формуле выше составляем схему (рис. 3.1), на которой С_1н = 3,349;

L_2н = 0,712; С_3н = 3,349; R_г.н = R_н.н = R_нор.



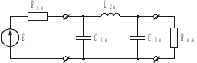
Рисунок 3.1
Денормируем элементы схемы НЧ - прототипа, используя соотношения (3.11) [1]:



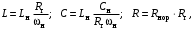
где f_нор = f_п.нч = 39,474 кГц – нормирующая частота;

R_г = 1000 Ом – нормирующее сопротивление, равное внутреннему сопротивлению источника сигнала.

Используя соотношения (3.11) и значения _н иR_г получаем реальные значения элементов схемы НЧ - прототипа:

;

---

.

2. 
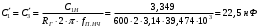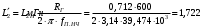   3.2. Расчёт элементов схемы
   

Из теории фильтров известно [1], что между частотами НЧ - прототипа и частотами _пф полосового фильтра существует соотношение

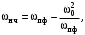где ₀ находится по (2.1). (3.8)

На основании (3.12) индуктивное сопротивление НЧ - прототипа заменяется сопротивлением последовательного контура с элементами

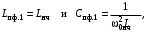(3.9)

а емкостное сопротивление НЧ - прототипа заменяется сопротивлением параллельного контура с элементами





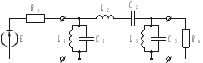
Рисунок 3.2 Принципиальная схема ПФ
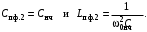(3.10)
Тогда, на основании схемы ФНЧ, изображенной на рис. 3.1 составляется схема полосового фильтра так, как это показано на рис. 3.2. Элементы этой схемы рассчитываются по формулам (3.13) и (3.14) [1]:



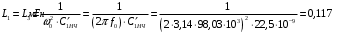
С₁ = С₃ = С'_1НЧ= 22,5 нФ, L₂ = L_2НЧ= 1,722 мГн,

.
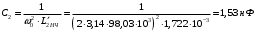Согласно шкале номинальных значений ряда Е24 элементы фильтра имеют следующие параметры:

L1 = L3 = 0,120 мГн ± 5 %; C1= C3 = 22 нФ ± 5 %;

L2 = 1,8 мГн ± 5 %; C2 = 1,5 нФ ± 5 %.


4.Активный АRC – фильтр

4.1 Расчёт полюсов

При аппроксимации синтеза ARC-фильтра воспользуюсь результатами расчета LC-фильтра, полученными в разделах 1-3. Причем, не самой нормированной передаточной функцией, а только ее полюсами (2.6):



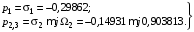
Находим полюсы денормированной передаточной функции ПФ.

Вначале находим:

---

Затем сами полюсы определяю по формуле:



























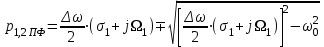
Расчет показывает, что вместо трёх полюсов нормированной передаточной функции НЧ - прототипа получается шесть полюсов передаточной функции ARC полосового фильтра, причем денормированной.

4.2. Формирование передаточной функции

Учитывая, что ARC-фильтры обычно строятся из каскадно-соеди­ненных звеньев второго порядка, целесообразно передаточную функцию таких фильтров формировать из произведения сомножителей тоже второго порядка. Они имеют вид:



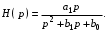
Тогда вся передаточная функция рассчитываемого фильтра будет:



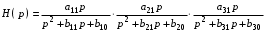
Коэффициенты в числителе могут иметь одинаковую величину и рассчитываться по формуле

---

Коэффициенты в знаменателе Н(р) находятся по формулам:

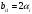и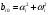

где 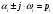– значение полюсов.

Рассчитываем эти коэффициенты:













Подставляя найденные коэффициенты в формулу Н(р), получим:



(4.5)

---