Файл: Расчет электрических фильтров.docx

---

4.3. Расчет элементов схемы фильтра
В качестве типовой выбираем простейшую схему ПФ на одном операционном усилителе (ОУ) (рис. 4.1).


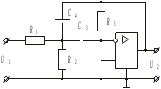
Рисунок 4.1

Если составить эквивалентную схему, заменив ОУ ИНУНом, то, используя любой из методов анализа цепей [1], можно получить передаточную функцию, описывающую работу схемы на рис. 4.1, в виде

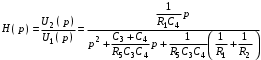(4.6)

Из (4.6) видно, что рассмотренная схема является схемой второго порядка. Следовательно, для реализации функции (4.5) потребуется три подобных схемы или три звена, соединенных каскадно. Расчет элементов этих схем R₁; R₂; С₃; С₄; R₅ ведется путем сравнения идентичных коэффициентов в формулах (4.5) и (4.6).

Для первого звена ПФ берутся коэффициенты из первого сомножителя (4.5). В системе пять неизвестных и только три уравнения. Система нерешаема. Поэтому задаёмся значениями емкостей конденсаторов С₃ и С₄ (в ходе настройки фильтра при его изготовлении принято использовать переменные сопротивления, т. к. переменных конденсаторов с большой емкостью нет вообще).

Если принять С₃ = С₄ = 2 нФ первого звена, то решая, получим:

---

Составляя аналогичную систему для второго звена при тех же С₃ = С₄ = 2 нФ,

получим:







Аналогично для третьего звена:











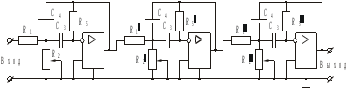
R₁, R₂, R₅ – сопротивления 1-го звена

R₁, R₂, R₅ – сопротивления 2-го звена

R₁, R₂, R₅ – сопротивления 3-го звена

Рисунок 5.2

На рисунке 5.2 представлена принципиальная схема активного фильтра.

Рисунок 5.2

4.4 Проверка результатов расчёта

Проверка расчетов может быть выполнена в двух этапах. Первый этап – проверяется только аппроксимация насколько точно созданная передаточная функция соответствует исходным требованиям к фильтру по ослаблению в ПП и в ПН. Второй этап – проверяется точность расчета, когда по известной передаточной функции схемы фильтра ( с учетом значений элементов схемы) рассчитывается и строится график H(f) или А(f) всей схемы фильтра и анализируется, насколько точно этот график соответствует исходных требованиям по ослаблению в ПП и в ПН. Второй этап для разработчика наиболее важнее.

При синтезе пассивного полосового фильтра получена передаточная функция только НЧ - прототипа (2.7) и в этом случае возможен только первый этап проверки. При синтезе активного ПФ известна передаточная функция одного звена схемы фильтра (4.6). Очевидно, что Н (

---

р) всего фильтра будет:

15Equation Section 5 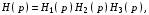(4.8)

где значения каждого сомножителя будут отличаться из-за разницы в значениях сопротивлений звеньев фильтра. Итак, формула (4.10) позволяет реализовать второй вариант проверки выполненных расчетов.

С этой целью в (4.5) производится замена переменной вида р = j, в результате чего получают выражение:



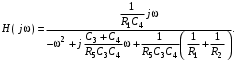
Находится модуль H(j) в виде:

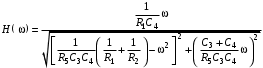(4.9)

Зная H(), легко найти зависимость ослабления от частоты вначале каждого звена, а затем всего фильтра:

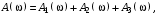(4.10)

где

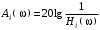(4.11)

В качестве числового примера выполним расчет первого звена фильтра.

Из раздела 4.3 берем значения элементов:

С₃ = С₄ = 2 нФ, R₁ = 3,3 кОм, R₂ = 51 Ом, R₅ = 13 кОм.

Подставляем эти значения в (4.9)



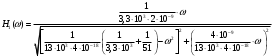
Значения элементов второго звена: R₁^/ = 3,3 кОм; R₂^/ = 20 Ом; R₅^/ = 22 кОм.



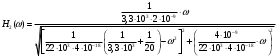
Значения третьего звена фильтра: R₁^// = 3,3кОм; R₂^{/ /}= 30 Ом; R^//₅ = 33 кОм.


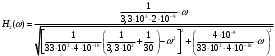
На частоте границы ПП f_п2 =119,737 кГц находим Н₁(_п2) = 0,604 . На частоте границы ПН f_з2 = 126,316 кГц находим Н₁(_з2) = 0,482. Кроме того находим Н₁() на частотах f_п1 = 80,263 кГц и f_з1 = 76,085 кГц. Результаты расчётов сведены в таблицу 4.3. Аналогичные расчеты выполняем для второго и третьего звеньев. Ослабления рассчитываются по формулам (4.10) и (4.11).

Если сравнивать рассчитанное ослабление всей схемы фильтра на частотах границ ПП и ПН с заданным ослаблением на этих же частотах (раздел 3.2), то можно сделать вывод о довольно хорошем их соответствии. При практическом изготовлении фильтров всегда предусматривается операция по их настройке, в ходе которой добиваются ослабления с требуемой точностью.

В ходе расчёта по формуле (4.9) видно, что значение Н() наиболее сильно зависит от величины сопротивления R₂

---

, поэтому именно это сопротивление выбираем переменным. По результатам расчётов строю график зависимости ослабления от частоты (рисунок 4.3).

Таблица 4.3

f, кГц	fз1	fп1	fп2	fз2
	76,085	80,263	119,737	126,316
Н1() Н2() Н3()	0,482 0,236 1,943	0,604 0,271 4,331	0,604 3,016 0,389	0,482 1,353 0,339
Н ()	0,221	0,708	0,708	0,221
А1(), дБ А2(), дБ А3(), дБ	6,333 12,552 –5,769	4,378 11,355 –12,733	4,378 -9,588 8,21	6,333 -2,624 9,407
А (), дБ	13,116	3,0	3,0	13,116

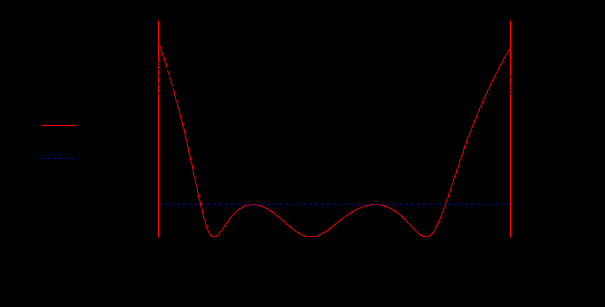
Рисунок 4.3 – Характеристика ослабления ПФ от частоты



Заключение

Мы рассчитали электрическую цепь, для этого выделив эффективную часть спектра периодических радиоимпульсов с помощью полосового фильтра, выполненного в двух вариантах – по схеме пассивного LC-фильтра и по схеме активного RC-фильтра.

Также рассчитали и построили график А(f) и он соответствует исходным требованиям по ослаблению в ПП и в ПН, что доказывает правильность расчетов.
Список используемой литературы

1. Бакалов В.П., Рожков В.М., Сметанина М.И. Методические указания и

задания на курсовую работу «Расчёт электрических фильтров»

2. Бакалов В.П., Воробиенко П.П., Крук Б.И. Теория электрических цепей. Учебник – М.: Радио и связь, 1998. – 444 с.

---