Файл: Расчет электрических фильтров.docx

Федеральное агентство связи Федеральное государственное бюджетное образовательное учреждения высшего образования «Сибирский государственный университет телекоммуникаций и информатики» (СибГУТИ)

Кафедра теории электрических цепей

КУРСОВАЯ РАБОТА

Вариант 59

Тема: «Расчет электрических фильтров»

Выполнил:

Группа:

Номер студенческого билета:

Адрес электронной почты:

Проверил: _____________________

Новосибирск, 2020г.

Содержание

Введение

Электрические фильтры – это линейные четырехполюсники, обладающие избирательными свойствами: они предназначены для выделения из состава сложного электрического колебания частотных составляющих определенного спектра частот, лежащего в полосе пропускания (ПП), и подавления тех составляющих, частоты которых лежат за пределами ПП, т. е. в полосе непропускания (ПН) или полосе задерживания (ПЗ). Между этими полосами находится переходная область.

Синтез (расчет) фильтров состоит из двух этапов: этапа аппроксимации и этапа реализации. На первом этапе по заданным максимальному и минимальному ослаблению в ПП и ПН формируется передаточная функция фильтра, т. е. математическое описание цепи, которая удовлетворяет указанным выше требованиям. На втором этапе создают схему цепи и определяют значения ее элементов по полученной передаточной функции.

В курсовой работе мы решаем конкретную техническую задачу – расчет электрической цепи для выделения эффективной части спектра периодических радиоимпульсов с помощью полосового фильтра, выполненного в двух вариантах – по схеме пассивного LC-фильтра и по схеме активного RC-фильтра.

Техническое задание

На входе полосового фильтра (ПФ) действуют периодические прямоугольные радиоимпульсы (рисунок 1.1) с параметрами:

---

1. 
   период следование импульсов Т_и = 220 мкс.
   
2. 
   длительность импульсов t_и = 80 мкс.
   
3. 
   период несущей частоты Т_н = 20 мкс.
   
4. 
   амплитуда колебаний несущей частоты Umн = 15 В, имеющего форму гармонического сигнала u(t) = Umн ^. cos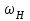 ^. t .
   

5) Сопротивление генератора радиоимпульсов R_Г сопротивление нагрузки R_H пассивного фильтра одинаковы R_Г = R_H = R = 1000 Ом. Характеристика фильтра аппроксимируется полиномом Чебышева.

6) Максимальное ослабление в полосе пропускания (ПП): А_max = 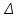A = 3 дБ;

7) Минимальное ослабление в полосе задерживания (ПЗ): A_min = 28 дБ.

Требуется рассчитать двухсторонне нагруженный пассивный полосовой LC- фильтр и активный RC –фильтр для выделения эффективной части спектра радиоимпульсов, лежащих в полосе частот от (f_Н-1/tи) до (f_Н+1/tи) (главный «лепесток спектра»). Примерный вид спектра приведён на рисунок 1.2.

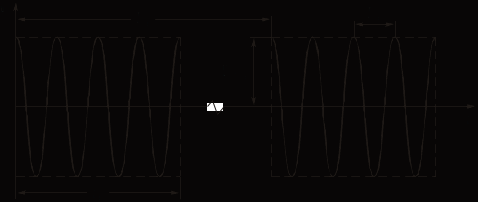
Рисунок 1.1


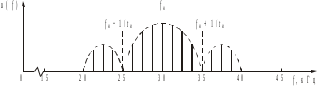
Рисунок 1.2

1.Построение амплитудного спектра радиоимпульсов

Прежде чем приступать к расчету фильтра, необходимо определить частотный состав сигнала, поступающего на вход фильтра, т. е. рассчитать и построить график амплитудного спектра периодических радиоимпульсов.

Вначале находится несущая частота:



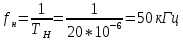
Затем рассчитываем частоты нулей огибающей спектра. Они зависят от длительности импульса:











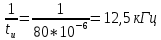
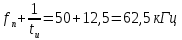
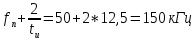
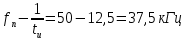
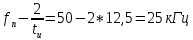
Максимальное значение огибающей в виде напряжения, соответствующее частоте

---

f_н, находится по формуле:



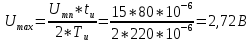
Зная максимальное значение и расположение нулей по оси частот, строим огибающую дискретного спектра периодических радиоимпульсов в виде пунктирной кривой в масштабе по оси частот (рис. 1.2).

Внутри огибающей находятся спектральные составляющие или гармоники спектра с частотами f_i, где i – номер гармоники. Они располагаются симметрично относительно несущей частоты, зависят от периода следования импульсов и находятся по формуле:

.

Учитывая, что

Рассчитаем скважность импульсного сигнала:

Рассчитываем частоты гармоник, лежащих только справа от f_н:













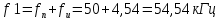
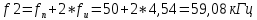
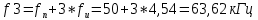
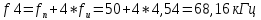
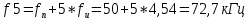
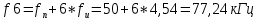
Частоты гармоник, лежащих слева от f_н, будут:












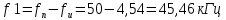
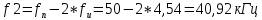
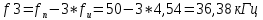
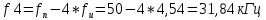
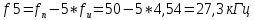
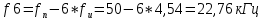
Амплитуды напряжения i-ых гармоник находятся по формуле:



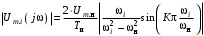
или



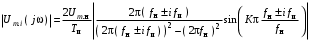
где K = t_и/T_н – количество периодов несущих колебаний синусоидальной формы в импульсе. Например, на рис. 1.1 К = 4. В нашем случае К = 80/20 = 4. Из анализа рис. 1.2 видно, что главный «лепесток спектра» занимает диапазон частот от 25 до 35 кГц. Крайние частоты диапазона совпадают с нулями огибающей, поэтому их амплитуды равны нулю, в частности

---

U_m.4 = 0, U_m.(–4) = 0. После расчёта амплитуд их значения отражаются в виде дискретных составляющих внутри огибающей спектра (рис. 1.2).

Приводим расчёты амплитуды для 1,2,3 гармоник:


































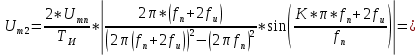
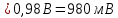
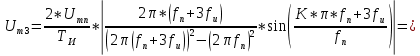
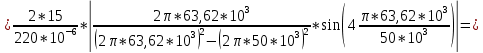
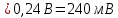
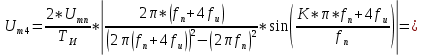
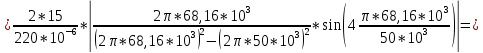
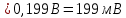
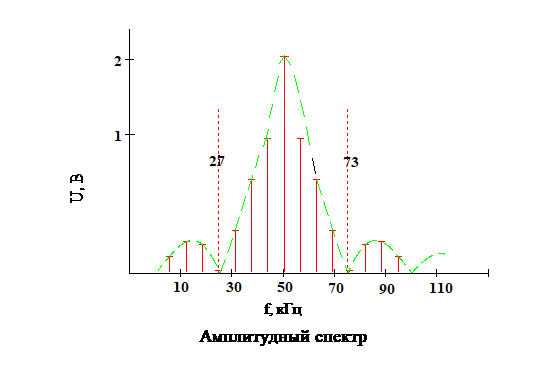
Рисунок 1.3

2.Формирование требований к полосовому фильтру

2.1. Расчёт граничных частот:

Электрические фильтры (рис.2.1) – это линейные четырехполюсники, обладающие избирательными свойствами: они предназначены для выделения из состава сложного электрического колебания частотных составляющих определенного спектра частот, лежащего в полосе пропускания (ПП), и подавления тех составляющих, частоты которых лежат за пределами ПП, т. е. в полосе непропускания (ПН) или полосе задерживания (ПЗ). Между этими полосами находится переходная область. Для ПФ полоса пропускания f_п1 f_п2 располагается между полосами непропускания 0 

---

f_з1 и f_з2  .


Рис.2.1

Синтез (расчет) фильтров состоит из двух этапов: этапа аппроксимации и этапа реализации. На первом этапе по заданным А_min и А_max в ПП и ПН формируется передаточная функция фильтра, т. е. математическое описание цепи, которая удовлетворяет указанным выше требованиям. На втором этапе создают схему цепи и определяют значения её элементов по полученной передаточной функции.

1 этап аппроксимации.

Учтём, что амплитуды спектральных составляющих на частотах 75,0 кГц и 125,0 кГц равны нулю, принимаем за эффективную часть спектра, которую нужно выделить ПФ, диапазон от 36,38 кГц до 63,62 кГц (см. рис.1.3). Граничную частоту полосы задерживания выбираю равной 1-ой гармоники спектра, находящейся после частоты 125,0 кГц; т.е. f₊₄ = f _З.2= 72,7 кГц. Используя формулу, нахожу центральную частоту ПП:


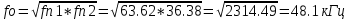
Тогда граничная частота полосы задерживания ПЗ определяется по формуле:


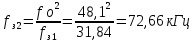
2.2. Расчёт ослабления

Минимально-допустимое ослабление фильтра в ПН зависит от разницы амплитуд гармоник 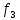и 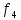спектра сигнала на выходе фильтра, выраженной в децибелах и заданной величиной 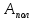– полного ослабления:



Amin=Aпол-А1=28-1,62=26,38 дБ



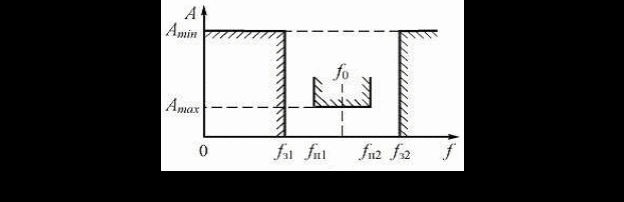
Рисунок 2.1

2.3. Расчёт порядка фильтра

Используя формулу, определяю ПП и ПЗ НЧ – прототипа:

fпнч=fп2-fп1=63,62-36,38=27,24 кГц

_{fзнч=fз2-fз1=68,16-31,84=36,32 кГц}

Требования к НЧ - прототипу могут быть проиллюстрированы рисунком 2.2.



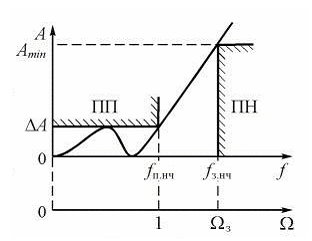
Рисунок 2.2

Находим коэффициент неравномерности ослабления фильтра в ПП при A =A и  = 1, когда (1) = Т_m(1) = 1:

---