Файл: Методология анализа и синтеза информационных систем.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 32
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное
учреждение высшего образования
«Воронежский государственный лесотехнический университет
имени Г.Ф. Морозова»
Кафедра вычислительной техники и информационных систем
Пояснительная записка
курсовой работы
на тему «Методология анализа и синтеза информационных систем»
09.03.02 Информационные системы и технологии
По дисциплине «Теория информационных процессов и систем»
| Студент группы _ИС2-191-ЗБ___ (номер группы) Руководитель, _к.т.н.___________ (ученая степень, ученое звание) | ___________ (подпись) __________ (подпись) | А.В.Зверев (инициалы и фамилия) В.Г.Горбунов (инициалы и фамилия) |
Воронеж 2022
Содержание
Введение 3
1.Теоретическая часть 5
1.1 Графические представления 5
1.2 Представления операций во времени 9
1.3 Структурно-лингвистическое моделирование 10
2. Практическая часть 13
2.1 Бизнес-процесс функционирование гостиницы 13
Заключение 18
Библиография 19
Введение
Исторически случилось так, что первые работы по компьютерному моделированию были связаны с физикой, где с помощью моделирования решался целый ряд задач гидравлики, фильтрации, теплопереноса и теплообмена, механики твердого тела и т. д.
Моделирование в основном представляло собой решение сложных нелинейных задач математической физики с помощью итерационных схем (за исключением разве тех задач, где использовался метод Монте-Карло), и по существу было оно, конечно, моделированием математическим. Успехи математического моделирования в физике способствовали распространению его на задачи химии, электроэнергетики, биологии и некоторых других дисциплин, причем схемы моделирования не слишком отличались друг от друга. Сложность решаемых с помощью моделирования задач всегда ограничивалась лишь мощностью имеющихся ЭВМ.
Надо заметить, что подобный вид моделирования весьма широко распространен и в настоящее время. Более того, за время развития методов моделирования на ЭВМ при решении задач фундаментальных и смежных предметных областей накоплены целые библиотеки подпрограмм и функций, облегчающих применение и расширяющих возможности моделирования. И все же в настоящее время понятие «компьютерное моделирование» обычно связывают не с фундаментальными дисциплинами, а в первую очередь с системным анализом — направлением кибернетики, впервые заявившим о себе в начале 50-х годов при исследовании сложных систем в биологии, макроэкономике, при создании автоматизированных экономико-организационных систем управления.
Системный анализ стремительно сформировался сначала в весьма модное направление науки об управлении сложными системами, а затем по мере развития — в методологию, а точнее, в нечто безбрежное, таинственное, доступное только самым могучим умам. Они с гордостью называли себя системными аналитиками и, как и положено после канонизации, возвышались над тысячами инженеров и программистов, работая в таинственных Институтах Системного Анализа Сложных, Очень Сложных и Совсем Сложных Систем, публикуя работы с названиями типа «Теория декомпозиции сингулярных, квазилинейных, иерархических макросистем рефлексивного типа». Однако по истечении некоторого времени обнаружилась странная особенность подобных работ: они существовали сами по себе, а многочисленные практические работы по системному анализу и управлению реальными объектами выполнялись сами по себе, без какой-либо связи с этими теоретическими изысканиями. Более того, обнаружилась странная особенность системного анализа: в чистом виде весь предмет может быть сведен к нескольким, интуитивно довольно прозрачным «принципам системного анализа», выглядящим как библейские заповеди, — принцип иерархичности, принцип единства целей, принцип эмерджентности и др.
1.Теоретическая часть
1.1 Графические представления
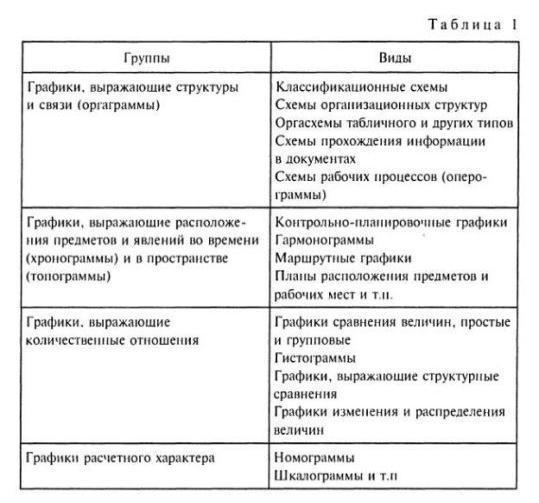
Графические представления рассматриваются здесь как класс методов формализованного представления систем, а так же, как основа возникновения СЛМ. В классификации Ф.Е. Темникова этот класс символически представлен рисунком.

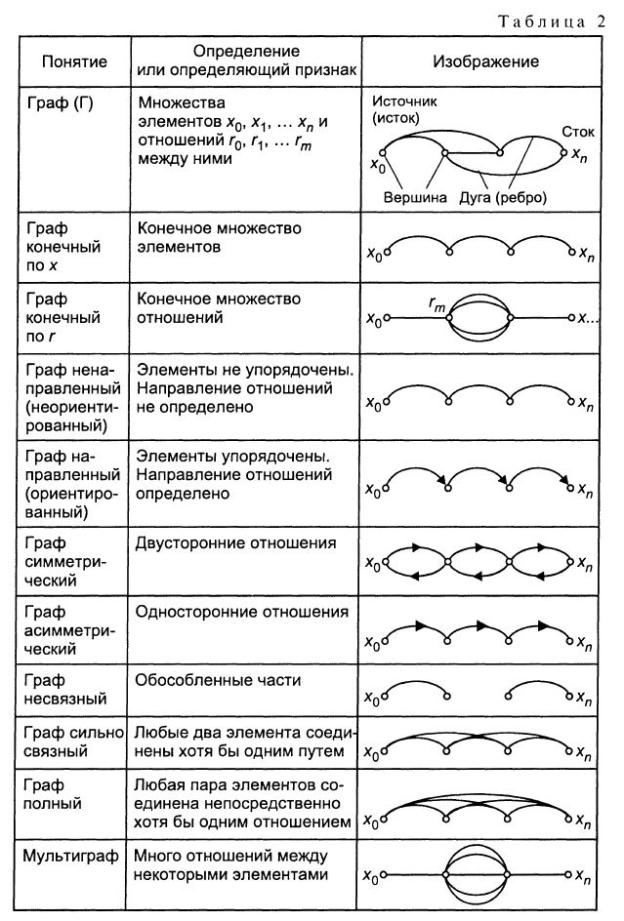
Понятие графа первоначально было введено Л.Эйлером. В классификации Темникова к классу графических представлений отнесены разнообразные средства: графы (в классическом понимании теории графов), структуры (древовидные, сетевые), гистограммы, диаграммы, графики.
Графические представления позволяют наглядно отображать структуры сложных систем и процессов, происходящих в них. С этой точки зрения они могут рассматриваться как промежуточные между методами формализованного представления систем и методами, направленными на активизацию использования интуиции и опыта специалистов.
Действительно, такие средства, как графики, диаграммы, гистограммы, можно отнести к средствам активизации интуиции специалистов.
Классификация применяемых графиков по признакам и видам приведена в табл. 1.
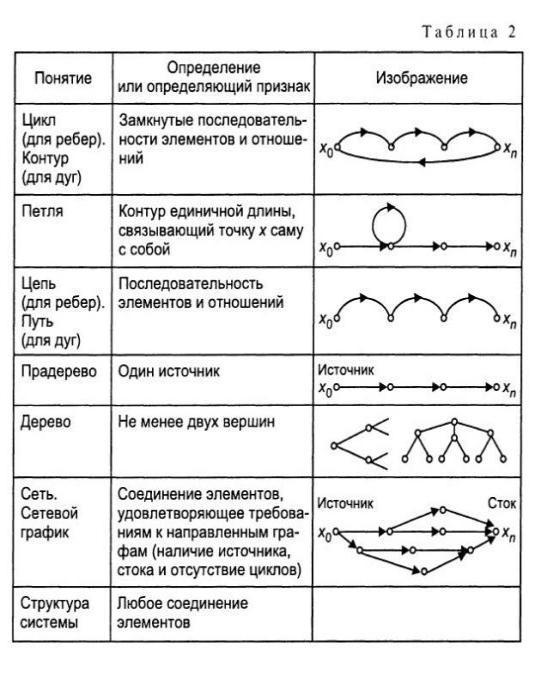
В то же время есть и возникшие на основе графических представлений методы, которые позволяют ставить и решать вопросы оптимизации процессов организации, управления, проектирования и являются математическими методами в традиционном смысле. Таковы, в частности, геометрия, теория графов. Основные понятия теории графов приведены в таблице 2, которая позволяет начать самостоятельное изучение теории графов.
граф ценность системный операция
1.2 Представления операций во времени
Особую роль в моделировании процессов в сложных системах проектирования и управления играют представления операций во времени. Старейшими из таких представлений являются графики Ганта, которые первоначально применялись при планировании, контроле и управлении производством.
Графики Ганта выполнялись в форме чертежей, ленточных диаграмм с ручным, а в последующем - и с автоматическим управлением. В последнем случае графики представляли собой ленты, одна половина которых была окрашена в черный цвет. Дальнейшим шагом было разделение лент на отрезки времени, отображающие дискретные операции, что позволяло обрабатывать дискретную информацию. Еще позже на этой основе возникли представления совокупности дискретных операций в дискретном времени как множества событий, упорядоченных в двух измерениях - сетевая структура.
В результате на этой основе возникли прикладные теории - PERT*, сетевого планирования и управления, а позднее - и ряд методов статистического сетевого моделирования с использованием вероятностных оценок графов. Первоначально СПУ широко применялись не только в управлении производственными процессами, но и в системах организационного управления. Однако в последнем случае важно понимать основные недостатки СПУ.
Во-первых, эта теория первоначально была ориентирована на анализ только одного класса графов - направленных (не имеющих обратных связей, т.е. циклов, петель; такие требования содержались в руководящих материалах по формированию сетевых планов предприятий), и это явилось одной из причин того, что впоследствии при применении сетевых методов для отображения ситуаций, не подчиняющихся этим ограничениям, был использован термин сетевое моделирование, снимающий требование однонаправленности графа.
Во-вторых (что наиболее существенно), при формировании сетевых планов необходимо участие высококвалифицированных специалистов, хорошо знающих процессы в системе (эту работу нельзя поручить техническим работникам, которые полезны лишь при оформлении сетевых графиков и обработке результатов оценки).
При этом по результатам исследования оказалось, что доля «ручного» труда лица, принимающего решение (ЛПР), при разработке сетевого графика составляет, по оценкам специалистов, до 95% общих затрат времени на анализ ситуаций и процессов с использованием сетевого моделирования. Для снижения доли «ручного» труда полезно сочетать графические представления с лингвистическими и семиотическими, разрабатывая языки автоматизации формирования сетевой модели. На основе такого сочетания методов возникло новое направление моделирования - структурно-лингвистическое.
1.3 Структурно-лингвистическое моделирование
СЛМ - подход, возникший в 70-е гг. XX в. в инженерной практике и основанный на использовании для реализации идей комбинаторики структурных представлений разного рода, с одной стороны, и средств математической лингвистики - с другой. В расширенном понимании подхода в качестве языковых (лингвистических) средств используются и другие методы дискретной математики (языки, основанные на теоретико-множественных представлениях, на использовании средств математической логики, семиотики).
В разных вариантах СЛМ используются разные средства. Общим для них является использование языкового (лингвистического) представления исходной информации и правил ее преобразования, т.е. понятий тезауруса, или словаря первичных терминов - элементов, из которых формируется модель, и грамматики - правил объединения элементов при ее формировании, и формы графического представления результатов моделирования. Поэтому в случае применения для реализации подобных моделей ЭВМ (и особенно при появлении средств, графического представления информации) можно сразу говорить не о
средствах структурно-лингвистического моделирования, а о разработке языка моделирования или автоматизации моделирования, языка автоматизации проектирования. Иногда это удобнее для пользователя, но разработчику такого языка полезно всеже исходить из основных положений СЛМ и использовать накопленный опыт создания таких моделей и средств их формирования и представления.
В основу формирования структурно-лингвистической модели могут быть положены средства: теоретико-множественных представлений, т.е. правила формирования пар, троек, пятерок из первичных элементов подмножеств; математическая логика, т.е. функция алгебр логики; математическая лингвистика; семиотические представления, допускающие произвольные правила, близкие к правилам естественного языка.
В зависимости от того, какие из этих направлений дискретной математики положены в основу языка, вместо термина «структурно-лингвистическое моделирование» используют другие термины - «графо-семиотическое», «сигнатурное» (знаковое) моделирование и т.п. Однако, учитывая, что все названные направления дискретной математики - теория множеств, математическая логика, математическая лингвистика, семиотика - отличаются одно от другого в основном исходными понятиями и видом отношений или правил комбинирования элементов, а общие принципы построения языков моделирования на их основе одинаковы, все подходы, сочетающие знаковые (в широком смысле) представления и графические (структурные), объединяют в единое направление - СЛМ.
Структурно-лингвистические модели могут быть многоуровневыми. На первом уровне моделей элементы могут объединяться в группы, образуя новые понятия, на следующем - эти новые понятия могут вступать в какие-либо отношения между собой, образуя еще более обобщенные компоненты модели, и т.д. При этом могут использоваться разные правила грамматики: на первом уровне это обычно правила типа «помещения рядом» (конкатенация, сцепление, формирование пар, троек, пятерок из элементов подмножеств исходного уровня модели), правила подстановки вместо одного элемента (символа, его обозначающего) нескольких; на последующих уровнях это могут быть операции типа «условного следования за», позволяющие формировать из компонентов предшествующего уровня модели принятия решений типа сетевых.
Структурно-лингвистический подход является хорошей основой для разработки моделей постепенной формализации модели принятия решения, которые должны базироваться на переменном использовании различных методов системного анализа - методов, направленных на активизацию использования интуиции и опыта специалистов, и методов формализованного представления систем.