Файл: Образовательная программа среднего профессионального образования Комплект контрольнооценочных средств по учебным.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 115
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
238 Глава 7
опустить, тогда по умолчанию тип доступа будет принимать значение
ReadWrite;
-
Считывание данных из текстового файла.
Для считывания данных из текстового файла используется класс
StreamReader, наследуемый от абстрактного класса TextReader. Он имеет сле-дующие основные конструкторы:
Sub New(ByVal pathAs String, ByVal encoding As Encoding)
Sub New(ByVal streamAs Stream, ByVal encoding As Encoding)
где:
path— полное имя файла, включающее само имя файла и путь к нему;
stream— поток для чтения;
encoding— кодировка знаков. Может принимать одно из значений пере-числения Encoding: ASCIIEncoding (Кодировка 7-разрядными ASCII-зна-ками), UnicodeEncoding (Кодировка в виде двух последовательных симво-лов), UTF7Encoding (Кодировка UTF-7) и UTF8Encoding(Кодировка UTF-8).
Параметр можно опустить.
Продемонстрируем примеры создания объекта класса:
Dim streamReader1 As New StreamReader ("C:\MyFile.txt")
Dim fileStream As New FileStream("C:\MyFile.txt", FileMode.Open)
Dim streamReader2 As New StreamReader(fileStream)
-
Запись данных в текстовый файл.
Класс StreamWriter, производный от абстрактного класса TextWriter, предна-значен для записи текстовых данных и имеет следующие основные конструк-торы:
Sub New(ByVal pathAs String, ByVal appendAs Boolean,
ByVal encodingAs Encoding)
Sub New(ByVal streamAs Stream, ByVal encoding As Encoding)
где:
path— полное имя файла, включающее само имя файла и путь к нему;
stream— поток для записи;
append— определяет, будет ли файл перезаписываться в случае указания
существующего файла. Если указано значение True, файл создается или
дописывается. Параметр можно опустить;
encoding— кодировка знаков. Может принимать одно из значений пере-числения Encoding: ASCIIEncoding(Кодировка 7-разрядными ASCII-зна-ками), UnicodeEncoding(Кодировка в виде двух последовательных симво-лов), UTF7Encoding(Кодировка UTF-7) и UTF8Encoding(Кодировка UTF-8).
Параметр можно опустить.
Продемонстрируем примеры создания объекта класса StreamWriter:
Dim streamWriter1 As New StreamWriter("C:\MyFile.txt", true)
Dim fileStream As New FileStream("C:\MyFile.txt", FileMode.Append)
Dim streamWriter2 As New StreamWriter(fileStream)
-
Открытие и создание файла для чтения и записи.
Для получения объектов классов FileStream, StreamReaderи StreamWriter
можно воспользоваться перечисленными в табл. 7.8 методами класса File.
Класс FileInfo имеет аналогичные методы за тем исключением, что имя фай-ла задается при создании экземпляра класса, и поэтому в методах параметр
Path отсутствует.
Эталоны ответов на теоретические задания: по дисциплине «Дискретная математика»
В формально-логических выводах используются истинные и ложные предложения. Определение: повествовательное предложение, о котором можно однозначно сказать, истинно оно или ложно, называется высказыванием. Примеры высказываний: "кит - животное", "все углы - прямые" и т. п. Первое из этих высказываний является, очевидно, истинным, а второе - ложным. Предложение "реши задачу", также как и "2+2", не является высказыванием. Определения математических понятий не являются высказываниями, т.к. это принятые соглашения. Будем обозначать высказывания большими латинскими буквами: A, B, C,…. Элементарные, нерасчленяемые высказывания будем называть атомами.Употребляемые в обычной речи логические связки "и", "или", "если..., то...", "эквивалентно", частица "не" и т. д. позволяют из уже заданных высказываний строить новые, более "сложные" высказывания. Аналогично тому, как в языке из простых предложений с помощью логических связок образуются сложные предложения, так и в логике высказываний из атомов можно образовывать составные высказывания. Истинность или ложность получаемых таким образом высказываний зависит от истинности и ложности исходных высказываний и соответствующей трактовки связок как операций над высказываниями. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
конъюнктивная нормальные формы Отрицанием высказывания A называется высказывание  (A), которое истинно, если A – ложно, и ложно, если A – истинно. (A), которое истинно, если A – ложно, и ложно, если A – истинно.Таблица истинности отрицания:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Конъюнкцией высказываний A и B называется высказывание A 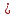 B (читается "A и B"), которое истинно тогда и только тогда, когда A, B – истинно. B (читается "A и B"), которое истинно тогда и только тогда, когда A, B – истинно.Таблица истинности конъюнкции:
Дизъюнкцией высказываний A и B называется высказывание A 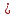 B (читается "A или B"), которое ложно тогда и только тогда, когда A, B – ложны. B (читается "A или B"), которое ложно тогда и только тогда, когда A, B – ложны.Таблица истинности дизъюнкции:
Импликацией высказываний A и B называется высказывание A→B (читается "если A, то B"), которое ложно тогда и только тогда, когда A – истинно, а B – ложно. Таблица истинности импликации:
Эквиваленцией высказываний A и В навивается высказывание, обозначаемое AB (читается :"A тогда и только тогда, когда В" или короче: "A эквивалентно В"), которое считается истинным только тогда, когда оба высказывания A и В имеют одинаковое истинностное значение. Эквивалентность АВ читается также следующим образом: "Для того, чтобы A, необходимо и достаточно, чтобы В". Таблица истинности эквиваленции:
7 – число простое; и.в. В: в равнобедренном треугольнике при основании углы равны, и.в. AВ - и.в.Логическая операция задается таблицей:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Законы логики (свойства логических операций)
Следующие формулы являются законами логики.
-
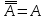 - закон двойного отрицания.
- закон двойного отрицания. -
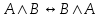 - закон коммутативности конъюнкции.
- закон коммутативности конъюнкции. -
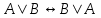 - закон коммутативности дизъюнкции.
- закон коммутативности дизъюнкции. -
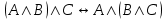 - закон ассоциативности конъюнкции.
- закон ассоциативности конъюнкции. -
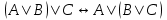 - закон ассоциативности дизъюнкции.
- закон ассоциативности дизъюнкции. -
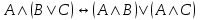 - закон дистрибутивности конъюнкции относительно дизъюнкции.
- закон дистрибутивности конъюнкции относительно дизъюнкции. -
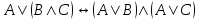 - закон дистрибутивности дизъюнкции относительно конъюнкции.
- закон дистрибутивности дизъюнкции относительно конъюнкции. -
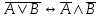 - закон отрицания дизъюнкции.
- закон отрицания дизъюнкции. -
 - закон отрицания конъюнкции.
- закон отрицания конъюнкции. -
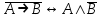 - закон отрицания импликации.
- закон отрицания импликации. -
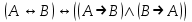 - закон выражения эквивалентности через конъюнкцию и импликацию.
- закон выражения эквивалентности через конъюнкцию и импликацию. -
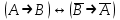 - закон контрапозиции.
- закон контрапозиции. -
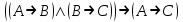 - закон силлогизма.
- закон силлогизма.
Отношения на множестве.
Если в декартовом произведении в качестве множества В выбрать множество А ( то есть А Х А= А
Для отношений на множестве вводятся понятия:
-
Обратное отношение-это множество пар (а,b) таких, что (b,a) А
А .
.
-
Дополнение-это множество пар (а,b) k.
k.
-
Тождественное отношение-множество пар (а, а) таких, что, а А,
А,
I= {(a, a), a
-
Универсальное отношение U={(a,b),a A, b
A, b А}
А}
Виды отношений:
-
Инъекция.
Е
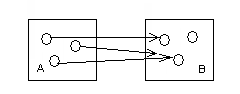 сли каждый элемент множества А соответствует элементу из множества В, то отношение f называется инъективным.
сли каждый элемент множества А соответствует элементу из множества В, то отношение f называется инъективным.Рис.2. Инъекция.
-
Сюръекция.
Если для каждого элемента y множества В существует элемент х
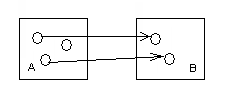
Рис.3.Сюръекция.
-
Биекция.
Если для каждого элемента y
Биективное отношение инъективно и сюръективно.
Биективное отношение имеет обратное отношение.
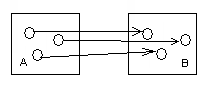
Рис.4. Биекция.