Файл: Образовательная программа среднего профессионального образования Комплект контрольнооценочных средств по учебным.docx

For j = 1 To n

For y = 1 To k

If Mid(x, y, 1) = Mid(i, j, k) Then s = s + 1

Next y

Next j

Next i

Case 2

s = 0

For i = 10 To 352

For j = 1 To k

If x = Mid(i, j, 2) Then s = s + 1

Next j

Next i

Case 3

s = 0

For i = 10 To 352

For j = 1 To k

If x = Mid(i, j, 3) Then s = s + 1

Next j

Next i

End Select

Text2.Text = s

End Sub

Private Sub Command2_Click()

Form5.Hide: Form6.Show

End Sub

Private Sub Command3_Click()

Form5.Hide: Form4.Show

End Sub
Задача № 6

1) Постановка задачи: Программа пересчитывает из кубического метра в галлон.

2)Интерфейс задачи:


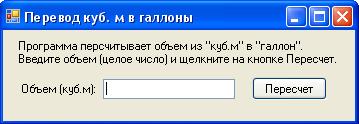
3) Листинг программы:

Dim S As Integer

Dim T As Integer

If Not IsNumeric(Vvod.Text) Then

MsgBox("Неверныйформатзаписи!", MsgBoxStyle.OkOnly, Title:="Ошибка")

Else

S = Vvod.Text

T = S * 264

Vvod.Text = T

End If

Задача № 7

1) Постановка задачи: Программа пересчитывает из литра в галлон.

2)Интерфейс задачи:


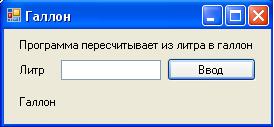
3)Листинг программы:

Dim L, G As Double, dial As DialogResult

If Not IsNumeric(TextBox1.Text) Then

MessageBox.Show("неправильныйформат")

TextBox1.Focus()

Else

L = TextBox1.Text

G = L / 3.78541178

Label4.Text = G

End If

dial = MessageBox.Show("хотитепосчитатьещераз?", "Выйти", MessageBoxButtons.YesNo, MessageBoxIcon.Asterisk)

If dial = DialogResult.Yes Then

TextBox1.Text = ""

Label4.Text = ""

Else

Application.Exit()

EndIf

Задача № 8

1) Постановка задачи: Программа пересчитывает из метров в футы.

2)Интерфейс задачи:


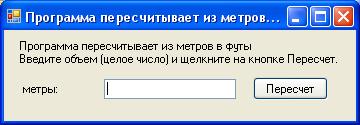
3)Листинг программы:

Dim S As Double

Dim T As Double

If Not IsNumeric(Vvod.Text) Then

MsgBox("Неверныйформатзаписи!", MsgBoxStyle.OkOnly, Title:="Ошибка")

Else

S = Vvod.Text

T = S * 0,305

Vvod.Text = T

End If

Задача № 9

1) Постановка задачи: Программа пересчитывает из аршина в метр.

2)Интерфейс задачи:


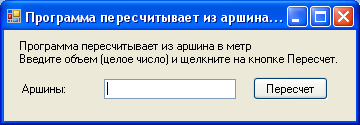
3)Листинг программы:

Dim S As Double

Dim T As Double

If Not IsNumeric(Vvod.Text) Then

MsgBox("Неверныйформатзаписи!", MsgBoxStyle.OkOnly, Title:="Ошибка")

Else

S = Vvod.Text

T = S * 1.28

Vvod.Text = T

End If

Задача № 10

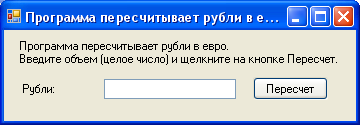
1) Постановка задачи: Программа пересчитывает рубли в евро.

2)Интерфейс задачи:


3)Листинг программы:

---

Dim S As Double

Dim T As Double

If Not IsNumeric(Vvod.Text) Then

MsgBox("Неверныйформатзаписи!", MsgBoxStyle.OkOnly, Title:="Ошибка")

Else

S = Vvod.Text

T = S * 50

Vvod.Text = T

End If

Задача № 11

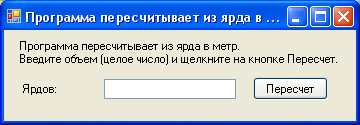
1) Постановка задачи: Программа пересчитывает из ярда в метр.

2)Интерфейс задачи:


3)Листинг программы:

Dim S As Double

Dim T As Double

If Not IsNumeric(Vvod.Text) Then

MsgBox("Неверныйформатзаписи!", MsgBoxStyle.OkOnly, Title:="Ошибка")

Else

S = Vvod.Text

T = S * 1.905

Vvod.Text = T

End If

Задача № 12

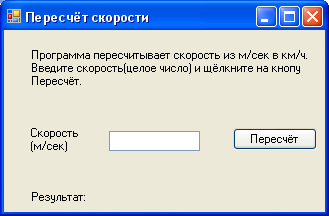
1) Постановка задачи: Программа пересчитывает скорость ветра из м/с в км/ч.

2)Интерфейс задачи:


3)Листинг программы:

Dim SkorostAs Integer

Dim rezult As Integer
If Not IsNumeric(txtVvod.Text) Then

MessageBox.Show("Ошибка!", "ПРоверкаошибки", MessageBoxButtons.OK, MessageBoxIcon.Stop)

Else

Skorost = txtVvod.Text

rezult = Skorost * 360

lblResult.Text = rezult

EndIf

Задача № 13

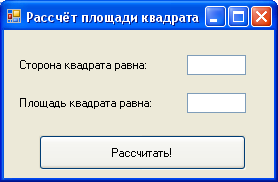
1) Постановка задачи: Программа рассчитывает площадь квадрата.

2)Интерфейс задачи:


3)Листинг программы:

Private Sub Button1_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button1.Click

Dim Side As Integer

Side = TextBox1.Text

Label1.Text = Square(Side)

'By value, ByVal, by reference ByRef

End Sub

Function Square(ByVal a As Integer) As Integer

Square = a ^ 2

End Function
Задача № 14

1) Постановка задачи: Программа рассчитывает значение по заданной формуле.

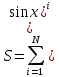
2)Интерфейс задачи:


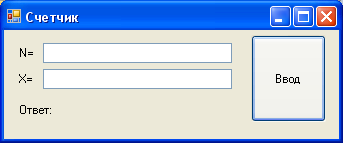
3)Листинг программы:

Dim N As Long, x, S1, S As Single

Dim k As Integer

Dim i As Integer

Dim dial As DialogResult
Public Sub Button1_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button1.Click

If Not IsNumeric(TextBox1.Text) Or Not IsNumeric(TextBox2.Text) Then

MessageBox.Show("неправильныйформат")

TextBox1.Focus()

TextBox2.Focus()

Else

S1 = 1

N = TextBox1.Text

x = TextBox2.Text

For i = 0 To N

S1 = S1 * MATH.SIN(x)

Next i

Label4.Text = S

End If

EndSub
Задача № 15

1) Постановка задачи: Программа рассчитывает значение по заданной формуле.

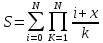
2)Интерфейс задачи:

---

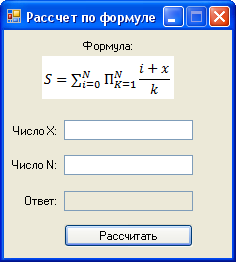
3)Листинг программы:

Private Sub Button1_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles ButtonRasschitat.Click

Dim i As Integer

Dim k As Integer

Dim N As Integer

Dim S As Double = 1

Dim S1 As Double

Dim x As Integer

If Not IsNumeric(TextBoxChisloN.Text) Or Not IsNumeric(TextBoxChisloX.Text) Then

MsgBox("Неверныйформатзаписи!")

Else

N = TextBoxChisloN.Text

x = TextBoxChisloX.Text

For i = 0 To N

For k = 1 To N

S = S * ((i + x) / k)

Next k

S1 = S1 + S

Next i
TextBoxOtvet.Text = S1

TextBoxOtvet.Text = (Format(S1, "#.##"))

EndIf

EndSub

Задача № 16

1) Постановка задачи: Программа рассчитывает значение по заданной формуле.

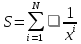
2)Интерфейс задачи:


3)Листинг программы:

Dim N As Long, x, S1, S As Single

Dim k As Integer

Dim i As Integer

Dim dial As DialogResult
Public Sub Button1_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button1.Click

If Not IsNumeric(TextBox1.Text) Or Not IsNumeric(TextBox2.Text) Then

MessageBox.Show("неправильныйформат")

TextBox1.Focus()

TextBox2.Focus()

Else

S1 = 1

N = TextBox1.Text

x = TextBox2.Text

For i = 0 To N

S1 = S1 + (1/x^i)

Next i

Label4.Text = S1

EndIf

EndSub

Задача № 17

1) Постановка задачи: Программа рассчитывает значение по заданной формуле.

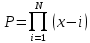
2)Интерфейс задачи:


3)Листинг программы:

Dim N As Long, x, S1, S As Single

Dim k As Integer

Dim i As Integer

Dim dial As DialogResult
Public Sub Button1_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button1.Click

If Not IsNumeric(TextBox1.Text) Or Not IsNumeric(TextBox2.Text) Then

MessageBox.Show("неправильныйформат")

TextBox1.Focus()

TextBox2.Focus()

Else

S1 = 1

N = TextBox1.Text

x = TextBox2.Text

For i = 1 To N

S1 = S1 *(x-i)

Next i

Label4.Text = S1

EndIf

EndSub
Теоретические задания: по дисциплине «Дискретная математика»

Составные высказывания

Основные логические операции. Формулы логики. Дизъюнктивная конъюнктивная нормальные формы

Построение таблицы истинности для формулы логики

Изучение законов логики. Равносильные преобразования.

Упрощение формул логики с помощью равносильных преобразований.

Булевы функции.

Совершенная дизъюнктивная и конъюнктивная нормальные формы (СДНФ и СКНФ)

Представление булевой функции в виде совершенной ДНФ и КНФ, минимальной КНФ, полинома Жегалкина

Понятие полноты множества функций. Замкнутые классы

Проверка булевой функции на принадлежность к замкнутым классам, на полноту.

Множества и подмножества.

Операции над множествами

Понятие предикат.

Логические операции над предикатами.

Определение логического значения для высказываний

Построение отрицаний к предикатам.

Понятие бинарного отношения и его свойства.

Отношение эквивалентности.

Исследование бинарных отношений на рефлексивность, симметричность и транзитивность; выделение классов эквивалентности

Композиция отображений

Операции над подстановками

Решение задач на запись циклического разложения подстановки

Выполнение операций и решение простейших уравнений в алгебре подстановок.

Понятие вычета по модулю N. Операции над вычетами. Шифрование

Метод математической индукции

Решение задач на выполнение операций в алгебре вычетов

Генерирование К-элементных подмножеств данного множества

Понятие графа. Способы задания графа. Методика выделения компонента связности в графе

Распознавание мостов и разделяющих вершин в графе

Нахождение расстояния между вершинами в графе.

Изоморфные графы. Эйлеровы графы

Плоские графы. Деревья и их свойства

Проверка графа на плоскость.

---

Практические задания: по дисциплине «Дискретная математика»

Задачи с решениями.

Задача №18

Между планетами введено космическое сообщение по следующим маршрутам: З-К, П-В, З-П, П-К, К-В, У-М, М-С, С-Ю, Ю-М, М-У. Можно ли добраться с З до М?

Решение:

Составим схему-граф маршрутов:



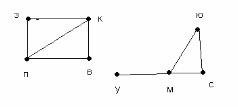
Мы видим, что от З до М добраться нельзя.
Задача №19

25 борцов играют по олимпийской системе (проигравший выбывает). За какое наименьшее количество встреч можно определить победителя?

Решение:

После каждой встречи 1 боец выбывает, в конце останется только один боец, значит наименьшее количество встреч 24.

Задача № 20

Аркадий, Борис. Владимир, Григорий и Дмитрий при встрече обменялись рукопожатиями (каждый пожал руку каждому по одному разу). Сколько всего рукопожатий было сделано?

Решение:

Пусть каждому из пяти молодых людей соответствует определенная точка на плоскости, названная первой буквой его имени, а производимому рукопожатию — отрезок или часть кривой, соединяющая конкретные точки — имена.


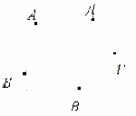
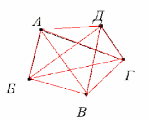
Если подсчитать число ребер графа, изображенного на рисунке справа, то это число и будет равно количеству совершенных рукопожатий между пятью молодыми людьми. Их 10.

Задача № 21

Кенигсбергские мосты.

К XVIII веку через реку, на которой стоял город Кенигсберг (ныне Калининград), было построено 7 мостов, которые связывали с берегами и друг с другом два острова, расположенные в пределах города ( см.рисунок)


Задача заключается в следующем: нужно пройти (если это возможно) по всем семи мостам так, чтобы на каждом из них побывать лишь по одному разу и вернуться к тому месту, откуда начал маршрут.

Решение:

Решить эту задачу удалось в 1736 г. Леонарду Эйлеру . В ходе решения задачи (после интерпретации условия задачи в виде графа, где вершины - острова и берега, а ребра - мосты, представленного на рисунке.)



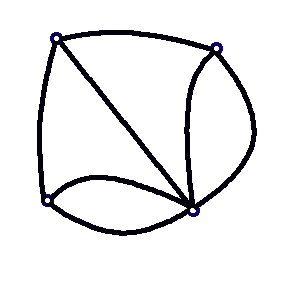
Прохождение по всем мостам при условии, что нужно на каждом побывать один раз и вернуться в точку начала путешествия, на языке теории графов выглядит как задача изображения «одним росчерком» графа, представленного на рисунке. Но, поскольку граф на этом рисунке имеет четыре нечетные вершины, то, согласно закономерности 7 такой граф начертить «одним росчерком» невозможно. Значит, и пройти по кенигсбергским мостам, соблюдая заданные условия,

---

нельзя.
Задача № 22

В трех различных домах живут три поссорившиеся между собой соседа. Недалеко от их домов имеются три колодца. Можно ли от каждого дома проложить к каждому из колодцев тропинку так, чтобы никакие две из них не пересекались?



Решение:

Построим граф, вершины которого
А, Б, В, 1, 2, 3
соответствуют домам и колодцам условия задачи, и попробуем доказать, что девятую тропинку — ребро графа, не пересекающее остальные ребра, провести нельзя.



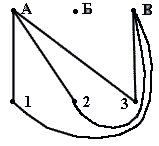
Проведенные в графе на рисунке ребра А1, А2, A3 и В1,В2, ВЗ (соответствующие тропинкам от домов А и В ко всем колодцам). Построенный граф разбил плоскость на три области: X, У, Z. Вершина Б, в зависимости от ее расположения на плоскости, попадает в одну из этих трех областей. Если вы рассмотрите каждый из трех случаев «попадания» вершины Б в одну из областей X, Y или Z, то убедитесь, что всякий раз одна из вершин графа 1, 2 или 3 (один из колодцев) будет «недоступной» для вершины Б (т. е. нельзя будет провести одно из ребер Б1, Б2 или Б3. которое не пересекло бы уже имеющихся в графе ребер).
Таким образом, ответ на вопрос задачи будет таким: «Нельзя!»

Задача № 23

---