Файл: Лабораторная работа 1 по теме Методы решения нелинейных уравнений.docx

Лабораторная работа 5.

Методы решения
обыкновенных дифференциальных уравнений»

5.1. Вопросы, подлежащие изучению

1. 
   Постановка задачи численного решения обыкновенных дифференциальных уравнений. Задача Коши.
   

1. 
   Методы Рунге-Кутты различных порядков, общие свойства.
   

2. 
   Погрешности методов.
   

2. 
   Выбор шага интегрирования.
   
3. 
   Графическая иллюстрация методов Рунге-Кутты.
   

5.2. Задание

1. 
   Выбрать индивидуальное задание в табл. 5-1 для решения обыкновенных дифференциальных уравнений:
   

4. 
   дифференциальное уравнение ;
   
5. 
   интервал [a;b] , где ищется решение дифференциального уравнения;
   
6. 
   начальные условия x0, y0;
   
7. 
   шаг интегрирования h0.
   
8. 
   Найти аналитическое решение заданного дифференциального уравнения, полагая его точным.
   
9. 
   Вычислить значения полученного решения на отрезке [a;b] с шагомh0.
   
10. 
    Найти численное решение дифференциального уравнения методом Эйлера - в точках отрезка [a;b] с шагом h0 с помощью «ручного счета».
    
11. 
    Вычислить значения погрешностей для , , .
    
12. 
    Составить схему алгоритма, написать программу интегрирования дифференциальных уравнений методом Рунге-Кутты 4-го порядка с автоматическим выбором шага и провести контрольное тестирование на примере, рассмотренном в п. 5.5.
    
13. 
    Получить решение с расчетом на ПК» с шагом h0 и E =10-4.
    
14. 
    Вычислить значения погрешностей ,
    
15. 
    Графически проиллюстрировать решения .
    

---

5.3. Варианты задания

Таблица 1.5-1

№ вар	Уравнение	x0	y0	h0	a	b
1	y' = x y2	0	-2	0.4	0	4
2	y' = y2 (x2+ x + 1)	0	-2	0.2	0	2
3	y' = x3 y2	0	-2	0.2	0	2
4	y' = y / cos2(x)	0	1	0.1	0	1
5	y' = y cos(x)	0	1	0.5	0	5
6	y' = y2cos(x)	0	-1	0.4	0	4
7	y' = x2 y + y	0	1	0.2	0	2
8	y' = (x – 1)2 y2	0	-1	0.5	0	5
9	y' = x3 y	0	1	0.2	0	2
10	y' = y2 sin(x)	0	0.5	0.2	0	2
11	y' = y sin(x)	0	1	0.4	0	4
12	y' = x y	0	1	0.2	0	2
13	y' = y2 / x	1	1	0.2	1	2
14	y' = x2 y	0	1	0.2	0	2
15	y' = y2 (2 – x)	0	-1	0.4	0	4
16	y' = 3 x2 y2	0	-4	0.2	0	2
17	y' = y2 (ex + 4x)	0	-1	0.4	0	4
18	y' = y (x – 1)	0	1	0.4	0	4
19	y' = x (1 + y2)	0	0	0.2	0	1.6
20	y' = x / (2y)	0	1	0.4	0	4
21	y' = y / (3 x2)	1	1	0.2	1	3
22	y' = 4 x e-3y	1	0	0.2	1	3
23	y' = 2 x y	0	1	0.2	0	2
24	y' = 2 x (y1/2)	0	1	0.4	0	4
25	y' = y2 ex	0	-2	0.4	0	4
26	y' = x (1 – y2)1/2	0	0	0.4	0	1.6
27	y' = (1 + x) y	0	1	0.2	0	2
28	y' = x2 (1 – y2)1/2	0	0	0.4	0	1.6
29	y' = (x2 + x) y2	0	-1	0.4	0	4
30	y' = y2 / cos2(x)	0	-1	0.3	0	1.5

---

5.4. Содержание отчета

1. 
   Индивидуальное задание.
   

16. 
    Решение ОДУ аналитическим методом.
    
17. 
    Значения полученного решения y(x) на отрезке [a;b] с шагом , записанные в табл. 5-2.
    
18. 
    Значения численного решения ОДУ, вычисленные методом Эйлера - в точках отрезка [a;b] с шагом h0, используя «ручной расчет», и записанные в табл. 5-2.
    
19. 
    Значения погрешностей для , , , записанные в табл. 5-2.
    
20. 
    Схема алгоритма, программа решения дифференциального уравнения методом Рунге-Кутты, результаты контрольного тестирования.
    
21. 
    Значения решения с шагом h0 и E =10-4 , полученные по программе, записанные в табл. 5-2 с указанием числа разбиений и фактического шага интегрирования для каждой точки.
    
22. 
    Значения вычисленных погрешностей , , записанные в табл. 5-2.
    
23. 
    Графическая иллюстрация решений .
    

Все решения в итоге должны быть оформлены в виде табл. результатов 5-2.

Таблица 5-2

xi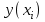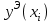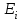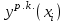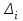
…	…	…	…	…	…

---

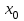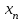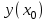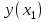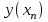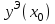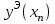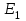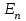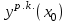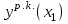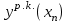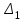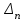5.5 Пример выполнения задания

2. 
   Задание для численного решения обыкновенных дифференциальных уравнений:
   

• 
  дифференциальное уравнение ;
  
• 
  интервал [0;1];
  
• 
  начальные условия x0=0, y0=1;
  
• 
  шаг интегрирования h0=0.1.
  

3. 
   Точное аналитическое решение заданного дифференциального уравнения
   

Найдем точное аналитическое решение заданного дифференциального уравнения (решение y=y(x)) методом разделения переменных. Для этого запишем уравнение в виде и проинтегрируем с учетом начальных условий. Получим . Из начальных условий следует, что с=0.

Аналитическое решение дифференциального уравнения .

4. 
   Значения точного решения ОДУ –y(x)
   

Вычислим значения полученного решения y(xi) на отрезке [0;1] с шагом изменения аргумента h=0.1:

xi	y(xi)
0	1
0.1	1.1051711
0.2	1.2214026
0.3	1.3498585
0.4	1.4918243
0.5	1.6487202
0.6	1.8221179
0.7	2.0137515
0.8	2.2255394
0.9	2.4596014
1	2.7182798

5. 
   Численное решение заданного ДУ методом Эйлера
   

Найдем значения численного решение ОДУ методом Эйлера (

---

)в точках отрезка[0;1]с шагом h=0.1. Для этого ДУ записывают в виде y’=f(x,y) . Тогда общая формула для определения очередного значения функции по методу Эйлера имеет вид yi+1=yi+hf(xi,yi), где , :

xi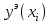
0
0.1	1.1000
0.2	1.210000
0.3	1.331000
0.4	1.4641001
0.5	1.6105101
0.6	1.7715611
0.7	1.9487172
0.8	2.1435795
0.9	2.3579478
1	2.5937426

6. 
   Значения погрешностей
   
7. 
   Вычислим значения погрешностей для , , :
   

   xi	Ei
   0
   0.1	0.005171
   0.2	0.011403
   0.3	0.018858
   0.4	0.027724
   0.5	0.038211
   0.6	0.050557
   0.7	0.065034
   0.8	0.081960
   0.9	0.101654
   1	0.124537

8. 
   Схема алгоритма и программа решения ОДУ методом Рунге-Кутты 4-го порядка с автоматическим выбором шага
   
9. 
   Схема алгоритма интегрирования ОДУ методом Рунге-Кутты 4-го порядка с автоматическим выбором шага приведена на рис.5.3-2 и рис. 5.3-3 в [2], а программу студенты должны написать самостоятельно.
   
10. 
    Решения, полученные по составленной программе «расчетом на ПК»
    
11. 
    Выполним программу и получим решение (то есть получим значения с шагом
    h= 0.1 и Е =10-4 ):
    

    xi
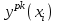
    0	1
    0.1	1.105171
    0.2	1.221403
    0.3	1.349859
    0.4	1.491825
    0.5	1.648721
    0.6	1.822119
    0.7	2.013753
    0.8	2.225541
    0.9	2.459603
    1	2.718282

12. 
    Значения погрешностей
    

---