Файл: Лабораторная работа 1 по теме Методы решения нелинейных уравнений.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 180
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
составить системы нормальных уравнений:
для линейной функции P1(x) = А0+А1*x система нормальных уравнений примет вид (линейная аппроксимация):
6*А0+9*А1 = 14.2
9*А0+10.2*А1 = 22.2
решить систему уравнений:
получим коэффициенты А0 = 0.438 и А1 = 1.286, тогда полином первой степени будет таким:
P1(x) = 0.438+1.286*x
-
Аппроксимация с помощью математического пакета
Осуществить аппроксимацию таблично заданной функции многочленом 1, 2, 3, 4 и 5-й степени.
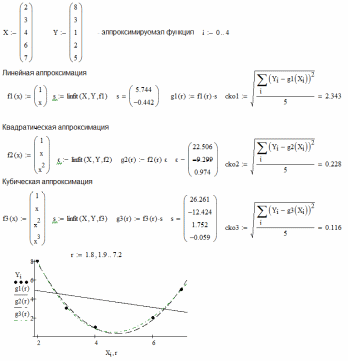
В этом примере рассмотрено использование функции linfit(x,y,f), где x,y- соответственно векторы значений аргументов и функции, а f – символьный вектор базисных функций. Использование этой функции позволяет определить вектор коэффициентов аппроксимации методом наименьших квадратов и далее невязку - среднеквадратическую погрешность приближения исходных точек к аппроксимирующей функции (сkо). Степень аппроксимирующего многочлена задается при описании символьного вектора f. В примере представлена аппроксимация таблично заданной функции многочленом 1, 2, 3, 4, 5-й степени, . Вектор s представляет собой набор аппроксимирующих коэффициентов, что позволяет получить аппроксимирующую функцию в явном виде.
Следует построить графики для полиномов 1, 2 и 5 степени.
Проанализировать изменение СКО в зависимости от степени полинома.
 |
Лабораторная работа по теме №4
«Численное интегрирование»
4.1. Вопросы, подлежащие изучению
-
Постановка задачи численного интегрирования. -
Методы прямоугольников, трапеций, Симпсона. -
Оценки погрешности численного интегрирования. Априорные, апостериорные. Правило Рунге. -
Графическая иллюстрация методов прямоугольников, трапеций и Симпсона.
4.2. Задание
-
Выбрать индивидуальное задание из табл.4-1 для численного интегрирования:
-
f(x) – подынтегральную функцию; -
a, b– пределы интегрирования; -
методы интегрирования для выполнения п.2 – значение в столбце tиm; -
начальный шаг интегрирования h0.
При этом значения в столбцах t и m означают: 1 –интегрирование методом средних прямоугольников, 2 – методом трапеций, 3 – методом Симпсона.
-
Вычислить интеграл по 1-му заданному методу, определяя значения (столбец m)из табл. 4-1, с шагом и
и  (
( и
и  ).
). -
Провести оценку погрешности полученных результатов по правилу Рунге. -
Написать программу для вычисления интеграла по 2-му заданному методу (столбец t из табл. 4-1) с точностями 10-2, 10-3, 10-4 . Получить результаты с точностями 10-2, 10-3, 10-4 -
Построить график зависимости числа разбиений отрезка от заданной точности. -
Вычислить заданный интеграл с использованием функции intg пакета Scilab.
4.3. Варианты задания
Таблица 4-1
| № | Подынтегральная функция | a | b | t | m | 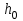 |
| 1 | f(x) = 8 e-x sin(-2x) | 2 | 3 | 1 | 3 | 0.25 |
| 2 | f(x) = e-x sin(2x) | 0 | 2 | 2 | 1 | 0.5 |
| 3 | f(x) = x3/2 – 2 x sin(x) | 3 | 4 | 3 | 2 | 0.25 |
| 4 | f(x) = e-xcos(-2x) | 2 | 4 | 1 | 3 | 0.5 |
| 5 | f(x) = cos(2x) + 2 sin(x) | 1 | 3 | 2 | 1 | 0.5 |
| 6 | f(x) = 8 sin(2x) – x | 0.2 | 1.2 | 3 | 2 | 0.25 |
| 7 | f(x) = 5 cos(-2x) e-x | -0.5 | 0.5 | 2 | 3 | 0.25 |
| 8 | f(x) = x sin(x + 1) – cos(x – 5) | 1 | 2 | 1 | 2 | 0.25 |
| 9 | f(x) = 0,25 x3 + cos(x/4) | 1 | 3 | 1 | 3 | 0,5 |
| 10 | f(x) = sin(2x) – 2 sin(x) | 3.5 | 5 | 1 | 3 | 0.5 |
| 11 | f(x) = sin(ex) – e-x +1 | 0 | 1 | 2 | 1 | 0.25 |
| 12 | f(x) = 5 x sin(x + 1) + 2 cos(x) | 1 | 2 | 1 | 2 | 0.25 |
| 13 | f(x) = 5 e-x + 4 x + x3/3 | -1 | 1 | 1 | 2 | 0.5 |
| 14 | f(x) = -2 sin(4x) ln(-x) + 5 | -2.5 | -1.5 | 1 | 3 | 0.25 |
| 15 | f(x) = sin(x – 1) – x cos(x + 3) | -4 | -2 | 3 | 1 | 0.5 |
| 16 | f(x) = 4 sin (x) – x1/2 | 1 | 2 | 2 | 3 | 0.25 |
| 17 | f(x) = 5 sin3(x) + cos3(x) | 1 | 2 | 2 | 1 | 0.25 |
| 18 | f(x) = cos(2x + 1) ln (2 / x) + 3 | 1 | 3 | 3 | 2 | 0.5 |
| 19 | f(x) = 3 cos(x2) / ln(x + 5) | -1 | 1 | 1 | 3 | 0.5 |
| 20 | f(x) = sin(x2) + 1 / (2 – x) | -1.5 | 0.5 | 2 | 1 | 0.5 |
| 21 | f(x) = x sin(x) + cos(x) + 5 | 0 | 2 | 1 | 2 | 0.5 |
| 22 | f(x) = – cos(x) – cos(2x) – x + 5 | 1 | 3 | 3 | 1 | 0.5 |
| 23 | f(x) = 1 + sin(4x) / ln(x) | 1.5 | 2.5 | 1 | 3 | 0.25 |
| 24 | f(x) = (1 + x2)1/2 + e-x | -1 | 2 | 2 | 1 | 0.75 |
| 25 | f(x) = sin(x + 1) e2 / x | 1 | 2 | 3 | 2 | 0.25 |
| 26 | f(x) = 2 (1 + x) e-x – 2 cos(x) | 1 | 4 | 2 | 3 | 0.75 |
| 27 | f(x) = – 8 sin(– x3) e-x | 0.4 | 1.4 | 1 | 3 | 0.25 |
| 28 | f(x) = – 10 sin(x3) cos(– x) | -1.4 | -0.4 | 2 | 1 | 0.25 |
| 29 | f(x) = x2cos(x + 3) – 4 | 3 | 4 | 3 | 1 | 0.25 |
| 30 | f(x) = – cos(x – 5) e2x / 3 | 1 | 3 | 1 | 3 | 0.5 |
4.4. Содержание отчета
-
Индивидуальное задание. -
Сценарий пакета Scilab для проведения расчета двумя заданными методами интегралов с шагом и
и  (
( и
и  ) и значения погрешностей по правилу Рунге.
) и значения погрешностей по правилу Рунге. -
Программа вычисления интеграла по 2-му заданному методу точностями 10-2, 10-3, 10-4 10-4. -
График полученной зависимости. -
Результаты решения, полученные с помощью функции пакета Scilab.
4.5. Пример выполнения задания
-
Задания для численного интегрирования:
-
 – подынтегральная функция;
– подынтегральная функция; -
a=1, b=3–пределы интегрирования; -
методы интегрирования – средних прямоугольников, трапеций, Симпсона; -
начальный шаг интегрирования h0=1.
-
Вычисление интегралов с шагом и
и  (
( и
и  ) и оценка его погрешности по правилу Рунге
) и оценка его погрешности по правилу Рунге
Правило Рунге применяют для вычисления погрешности путём двойного просчёта интеграла с шагами h/2 и h,при этом погрешность вычисляется по формуле
Полагают, что интеграл вычислен с точностьюЕ, если
– уточненное значение интеграла, p – порядок метода.
Вычислим интеграл по формуле
-
средних прямоугольников и оценим погрешность интегрирования методом двойного просчёта:
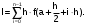

-
трапеций и оценим погрешность интегрирования методом двойного просчета:
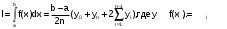

-
Симпсона и оценим погрешность интегрирования методом двойного просчета:
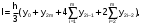 где
где 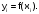

3.6. Вычисление определенных интегралов в Scilab
| --> deff('y=f(x)','y=log(x)'); --> a=1;b=3; --> [s,ir]=intg(a,b,f) ir = 1.439D-14 s = 1.2958369 |
Контрольные вопросы по теме
«Численное интегрирование»
-
Что такое шаг интегрирования? -
Каким образом связана задача численного интегрирования и интерполяция? -
Какое влияние оказывает уменьшение числа разбиений на отрезке [a;b] на погрешность интегрирования? -
Каким образом вычисляется определенный интеграл в случае, если подынтегральная функция задана таблицей с переменным шагом? -
Какой из изученных вами методов численного интегрирования обладает высшей степенью точности? -
Зависит ли точность численного интегрирования от величины шага интегрирования? -
Для чего предназначен метод двойного просчета? -
Что представляет собой формула для вычисления элементарного интеграла по формуле трапеций? -
Что представляет собой формула для вычисления элементарного интеграла по формуле Симпсона? -
Интерполяционным многочленом, какой степени заменяется подынтегральная функция в методе прямоугольников? -
Интерполяционным многочленом, какой степени заменяется подынтегральная функция в методе трапеций? -
В каком методе для вычисления интеграла необходимо выбирать количество интервалов разбиения кратное двум? -
Какой метод позволяет обеспечить вычисление интеграла с заданной точностью? -
Какой метод численного интегрирования даст наиболее точный результат, если подынтегральная функция имеет вид y = 5x3? -
В каком методе численного интегрирования подынтегральная функция заменяется квадратичным полиномом? -
Какой метод численного интегрирования даст точный результат, если подынтегральная функция имеет вид f(x) = x2? -
Какой метод интегрирования наилучшим образом подходит для вычисления интеграла линейной функции? -
Обеспечивают ли методы трапеций и метод средних прямоугольников точность одного порядка? -
Какой из известных вам методов интегрирования обладает наименьшей точностью? -
Сколько шагов интегрирования содержит элементарный отрезок интегрирования в методе Симпсона?