Файл: Контрольная работа по дисциплине Эконометрика Вариант 1 Содержание задача парная регрессия 2 задача множественная регрессия и корреляция 13.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 09.12.2023

Просмотров: 72

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Содержание

ЗАДАЧА 1. Парная регрессия

ЗАДАЧА 2. Множественная регрессия и корреляция

ЗАДАЧА 3. Временные ряды

ЗАДАЧА 3. Временные ряды


Имеются условные данные об изменении результирующего показателя 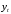для соответствующих моментов (уровней) времени t.

Требуется:

  1. Построить аддитивную модель временного ряда (для нечетных вариантов) или мультипликативную модель временного ряда (для четных вариантов),

  2. Сделать прогноз на 2 уровня вперед.

Дано: t- годы; yt – собственная продукция

t
1
2
3
4
5
6
7
8
9
10

yt
1,3
1,4
1,5
1,7
2,1
2,2
2,5
2,7
3,0
3,3

(вариант 1)

Под аддитивной моделью временного ряда подразумевают такую модель, в которой уровни ряда представлены как сумма трендовой (Т), сезонной или циклической (S) и случайной (Е) компонент:

уt=Т+S+Е.

Для того, чтобы построить аддитивную модель, для начала следует провести анализ структуры временного ряда, то есть определить наличие или отсутствие данных компонент в ряду динамики. Для определения структуруы временного ряда будем использовать автокорреляцию, заполнив вычислениями таблицы с 6 по 8.

Таблица 6 – Вычисление автокорреляции для временного ряда с лагом 1

t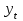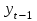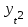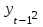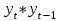










1
1,3
-
-
-
-

2
1,4
1,3
1,96
1,69
1,82

3
1,5
1,4
2,25
1,96
2,10

4
1,7
1,5
2,89
2,25
2,55

5
2,1
1,7
4,41
2,89
3,57

6
2,2
2,1
4,84
4,41
4,62

7
2,5
2,2
6,25
4,84
5,50

8
2,7
2,5
7,29
6,25
6,75

9
3,0
2,7
9,00
7,29
8,10

10
3,3
3,0
10,89
9,00
9,90

Итого Σ c 2 по 10
20,4
18,4
49,78
40,58
44,91

Среднее
2,3
2,0
5,53
4,51
4,99

Дисперсия
0,393
0,329
 
 
 

Среднее кв. откл.
0,627
0,574
 
 
 

Выведем коэффициент автокорреляции с лагом 1:



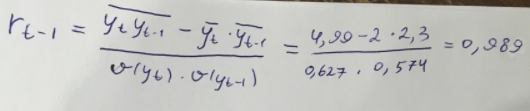
Таблица 7 – Вычисление автокорреляции для временного ряда с лагом 2

t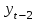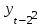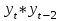










1
1,3
 -
- 
- 
- 

2
1,4
 -
 -
 -
 -

3
1,5
1,3
2,25
1,69
1,95

4
1,7
1,4
2,89
1,96
2,38

5
2,1
1,5
4,41
2,25
3,15

6
2,2
1,7
4,84
2,89
3,74

7
2,5
2,1
6,25
4,41
5,25

8
2,7
2,2
7,29
4,84
5,94

9
3,0
2,5
9,00
6,25
7,50

10
3,3
2,7
10,89
7,29
8,91

Итого Σ c 3 по 10
19,0
15,4
47,82
31,58
38,82

Среднее
2,4
1,9
5,98
3,95
4,85

Дисперсия
0,337
0,242
 
 
 

Среднее кв. откл.
0,580
0,492
 
 
 

Выведем коэффициент автокорреляции с лагом 2:



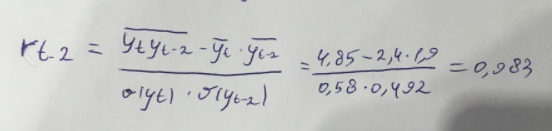
Таблица 8 – Вычисление автокорреляции для временного ряда с лагом 3

t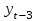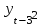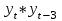










1
1,3
 -
 -
- 
- 

2
1,4
 -
 -
 -
 -

3
1,5
 -
 -
 -
 -

4
1,7
1,3
2,89
1,69
2,21

5
2,1
1,4
4,41
1,96
2,94

6
2,2
1,5
4,84
2,25
3,30

7
2,5
1,7
6,25
2,89
4,25

8
2,7
2,1
7,29
4,41
5,67

9
3,0
2,2
9,00
4,84
6,60

10
3,3
2,5
10,89
6,25
8,25

Итого Σ c 4 по 10
17,5
12,7
45,57
24,29
33,22

Среднее
2,5
1,8
6,51
3,47
4,75

Дисперсия
0,260
0,178
 
 
 

Среднее кв. откл.
0,510
0,422
 
 
 

Выведем коэффициент автокорреляции с лагом 3:



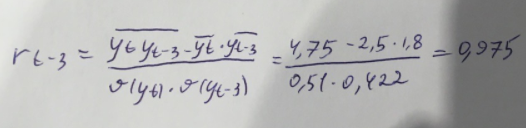
С увеличением лага на единицу число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается на 1. В таком случае следует использовать максимальный порядок коэффициента автокорреляции, равный n/4 (в данном случае: 3).

Анализ структуры ряда позволяет нам говорить, что наиболее высокое значение автокорреляции наблюдается при лаге = 1. Отсюда следует, что данный временной ряд содержит только тенденцию, циклические колебания отсутствуют.

Следующим шагом проведем построение уравнения тренда. Для этого будем заполнять таблицу 9

Таблица 9 – Вычисления для уравнения тренда

№
t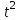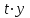








Т


1
1
1,3
1
1,69
1,3
1,14
0,025

2
2
1,4
4
1,96
2,8
1,37
0,001

3
3
1,5
9
2,25
4,5
1,60
0,010

4
4
1,7
16
2,89
6,8
1,83
0,016

5
5
2,1
25
4,41
10,5
2,06
0,002

6
6
2,2
36
4,84
13,2
2,28
0,007

7
7
2,5
49
6,25
17,5
2,51
0,000

8
8
2,7
64
7,29
21,6
2,74
0,002

9
9
3,0
81
9,00
27,0
2,97
0,001

10
10
3,3
100
10,89
33,0
3,20
0,010

Итого
55
21,7
385
51,47
138,2
21,70
0,074

Ср. знач.
5,50
2,17
38,50
5,15
13,82
2,17
0,007

Дисперсия
8,25
0,44
 
 
 
 
 

Среднее кв. откл.
2,87
0,66
 
 
 
 
 

Общий вид линейного уравнения тренда:



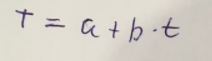
Используем метод наименьших квадратов для нахождения необходимых параметров:



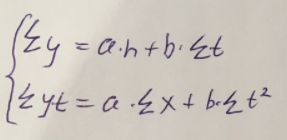
Теперь вычислим параметры:



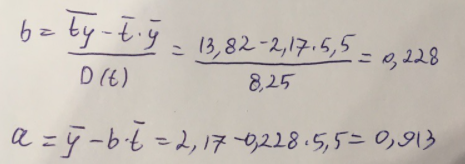
Тогда линейное уравнение тренда будет иметь вид:



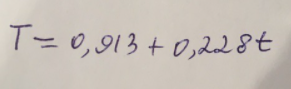
Дополним модель временного тренда расчетом ошибок Еi., заполнив новую таблицу 10.

Таблица 10 – Аддитивная модель временного тренда

№
t


Т
S
Е = y – (T+S)

1
1
1,3
1,14
0
0,16

2
2
1,4
1,37
0
0,03

3
3
1,5
1,60
0
-0,10

4
4
1,7
1,83
0
-0,13

5
5
2,1
2,06
0
0,04

6
6
2,2
2,28
0
-0,08

7
7
2,5
2,51
0
-0,01

8
8
2,7
2,74
0
-0,04

9
9
3,0
2,97
0
0,03

10
10
3,3
3,20
0
0,10

Итого
55
21,7
21,70
0
0,00

Ср. знач.
5,50
2,17
2,17
0
0,00

Смотрите также файлы