Файл: Контрольная работа по дисциплине Эконометрика Вариант 1 Содержание задача парная регрессия 2 задача множественная регрессия и корреляция 13.docx

Федеральное государственное образовательное бюджетное учреждение высшего образования

ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ

РОССИЙСКОЙ ФЕДЕРАЦИИ

Ярославский филиал Финуниверситета

Кафедра «Экономика и финансы»

Контрольная работа

по дисциплине «Эконометрика»

Вариант 1

Содержание

ЗАДАЧА 1. Парная регрессия

Требуется:

1. Для характеристики y от x построить следующие модели:

- линейную,

- экспоненциальную,

- гиперболическую.

2. Оценить каждую модель, определив:

- индекс корреляции,

- коэффициент детерминации,

- F-критерий Фишера.

3. Составить сводную таблицу вычислений, выбрать лучшую модель, дать интерпретацию рассчитанных характеристик.

4. По лучшей модели рассчитать прогнозные значения результативного признака, если прогнозное значение фактора увеличится на 10% относительно его среднего уровня.

5. На графике отобразить диаграмму рассеяния, график лучшей модельной кривой и прогнозное значение.

Дано:

х – имущество (в тыс. $) семи случайно выбранных семей,

у – накопления (в тыс. $).

x	60	36	36	15	90	45	70
y	3	6	5	3,5	1,5	4,5	2

(вариант 1)

Решение:

Выполним построение линейной модели

---

. Составим для этого таблицу 1. Для начала следует найти дисперсию и среднее квадратическое отклонение. Они помогут нам в решении задачи.

Таким образом, найдем дисперсию:



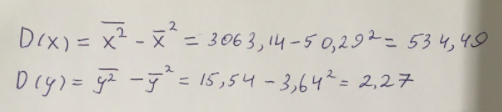
Далее выясним среднее квадратическое отклонение:



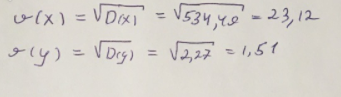
Таблица 1. – Вычисление для линейной модели зависимости накоплений (y) от имущества случайно выбранной семьи (x).

№
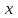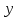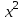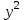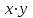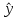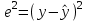1	60	3,0	3600	9,00	180,0	3,19	0,034
2	36	6,0	1296	36,00	216,0	4,32	2,836
3	36	5,0	1296	25,00	180,0	4,32	0,468
4	15	3,5	225	12,25	52,5	5,31	3,260
5	90	1,5	8100	2,25	135,0	1,77	0,074
6	45	4,5	2025	20,25	202,5	3,89	0,370
7	70	2,0	4900	4,00	140,0	2,71	0,510
Итого	352	25,5	21442	108,75	1106,0	25,50	7,551
Ср. знач.	50,29	3,64	3063,14	15,54	158,00	3,64	1,079

---

Линейное уравнение парной регрессии имеет вид:

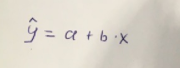
Используем метод наименьших квадратов для нахождения необходимых параметров:



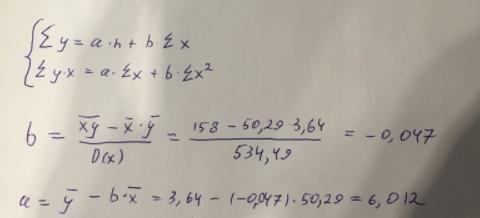
Итак, линейное уравнение парной регрессии будет:



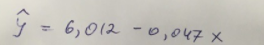
Найдем индекс корреляции для нахождения зависимости между показателями:



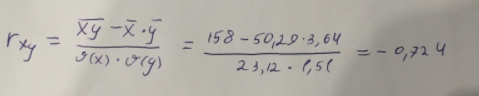
Мы видим, что значение индекса корреляции в диапазоне от 0,7 до 0,9. А значит можем сделать вывод о тесной линейной зависимости между накоплениями (y) и стоимость имущества семьи (x).

Далее выполним расчет коэффициента детерминации для оценки качества модели:



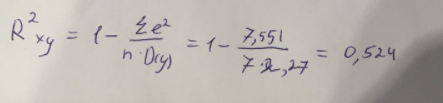
Значение коэффициента составляет 0,524. Также оно довольно сильно отклоняется от 1. Выводом для нас будет то, что мы не видим высокого качества линейной модели уравнения регрессии. К тоже она объясняет 52,4% вариации накоплений (значений y) в зависимости от изменения стоимости имущества семьи (x).

Найдем F-критерий Фишера для определения значимости уравнения:



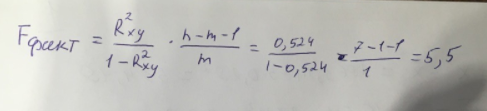
Табличное значение F-критерия мы найдем по таблице Фишера:

 = 0,05 (уровень значимости); к₁ = n – m – 1 = 7 – 1 – 1 = 5; к₂ = m = 1.

F_табл = 6,60

Теперь сравним фактическое и табличное значения F-критерия. Получим:

F_факт < F_табл (5,50 < 6,60)

Как итог, мы видим линейное уравнение регрессии не является значимым.

Выполним построение экспоненциальной модели. Составим для этого таблицу 2. Для начала следует найти дисперсию и среднее квадратическое отклонение. Они помогут нам в решении задачи.

Таким образом, найдем дисперсию:



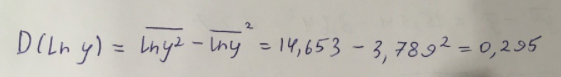
Далее выясним среднее квадратическое отклонение:



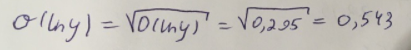
Таблица 2. – Вычисление для экспоненциальной модели зависимости накоплений (y) от имущества случайно выбранной семьи (x).

---

№
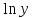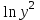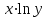1	60	1,099	3600	1,207	65,92	2,82	0,032
2	36	1,792	1296	3,210	64,50	4,15	3,411
3	36	1,609	1296	2,590	57,94	4,15	0,717
4	15	1,253	225	1,569	18,79	5,83	5,410
5	90	0,405	8100	0,164	36,49	1,74	0,057
6	45	1,504	2025	2,262	67,68	3,59	0,824
7	70	0,693	4900	0,480	48,52	2,40	0,161
Итого	352	8,355	21442	11,484	359,85	24,69	10,612
Ср. знач.	50,29	1,194	3063,14	1,641	51,41	3,53	1,516

---

Экспоненциальное уравнение парной регрессии имеет вид:



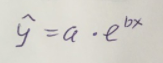
При этом линеаризация:



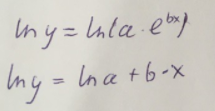
Используем метод наименьших квадратов для нахождения необходимых параметров:



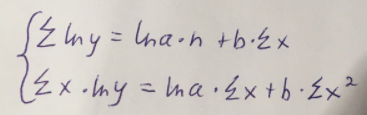
Следующим шагом найдем параметры:



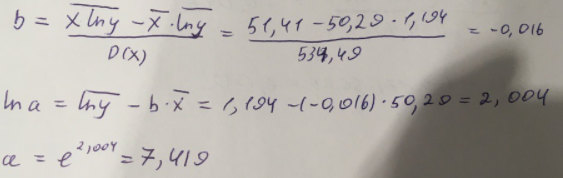
Итак, экспоненциальное уравнение парной регрессии будет:



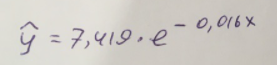
Найдем индекс корреляции для нахождения зависимости между показателями:



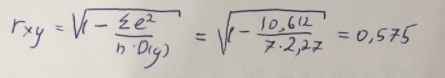
Мы видим, что значение индекса корреляции в диапазоне от 0,5 до 0,7. А значит в экспоненциальной модели мы можем сделать вывод о заметной зависимости между накоплениями (y) и стоимость имущества семьи (x).

Далее выполним расчет коэффициента детерминации для оценки качества модели:



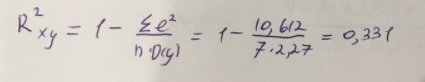
Значение коэффициента составляет 0,331. Также оно очень сильно отклоняется от 1. Выводом для нас будет то, что мы не видим высокого качества линейной модели уравнения регрессии. К тоже она объясняет 33,1% вариации накоплений (значений y) в зависимости от изменения стоимости имущества семьи (x).

Найдем F-критерий Фишера для определения значимости уравнения:



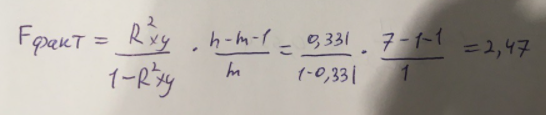
Табличное значение F-критерия мы найдем по таблице Фишера:

 = 0,05 (уровень значимости); к₁ = n – m – 1 = 7 – 1 – 1 = 5; к₂ = m = 1.

F_табл = 6,60

Теперь сравним фактическое и табличное значения F-критерия. Получим:

F_факт < F_табл (2,47 < 6,60)

Как итог, мы видим экспоненциальное уравнение регрессии не является значимым.

Выполним построение гиперболической модели

---