Файл: Контрольная работа по дисциплине Эконометрика Вариант 1 Содержание задача парная регрессия 2 задача множественная регрессия и корреляция 13.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.12.2023
Просмотров: 73
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
. Составим для этого таблицу 3. Для начала следует найти дисперсию и среднее квадратическое отклонение. Они помогут нам в решении задачи.
Таким образом, найдем дисперсию:
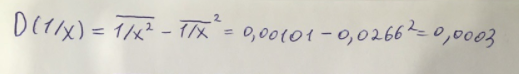
Далее выясним среднее квадратическое отклонение:
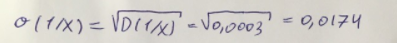
Таблица 3. – Вычисление для гиперболической модели зависимости накоплений (y) от имущества случайно выбранной семьи (x).
Гиперболическое уравнение парной регрессии имеет вид:
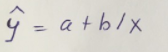
Используем метод наименьших квадратов для нахождения необходимых параметров:
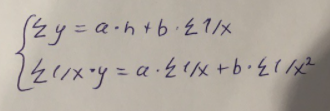
Следующим шагом найдем параметры:
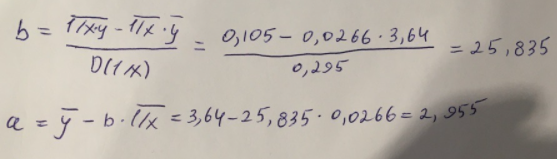
Итак, гиперболическое уравнение парной регрессии будет:
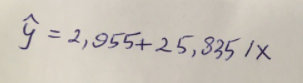
Найдем индекс корреляции для нахождения зависимости между показателями:
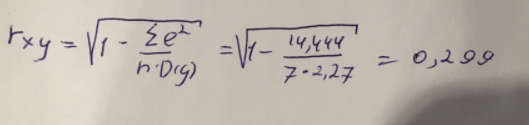
Мы видим, что значение индекса корреляции в диапазоне от 0,1 до 0,3. А значит в гиперболической модели мы можем сделать вывод о слабой зависимости между накоплениями (y) и стоимость имущества семьи (x).
Далее выполним расчет коэффициента детерминации для оценки качества модели:
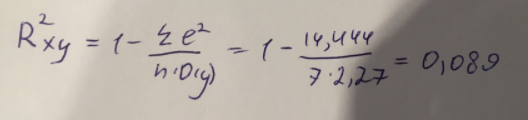
Значение коэффициента составляет 0,0,089. Также оно очень сильно отклоняется от 1. Выводом для нас будет то, что мы не видим высокого качества линейной модели уравнения регрессии. К тоже она объясняет 8,9% вариации накоплений (значений y) в зависимости от изменения стоимости имущества семьи (x).
Найдем F-критерий Фишера для определения значимости уравнения:
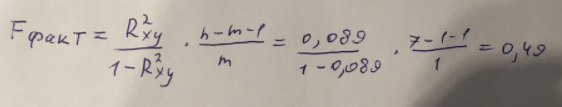
Табличное значение F-критерия мы найдем по таблице Фишера:
= 0,05 (уровень значимости); к1 = n – m – 1 = 7 – 1 – 1 = 5; к2 = m = 1.
Fтабл = 6,60
Теперь сравним фактическое и табличное значения F-критерия. Получим:
Fфакт < Fтабл (0,49 < 6,60)
Как итог, мы видим, что гиперболическое уравнение регрессии не является значимым.
Для последующего анализа и выведения итогов составим общую таблицу 4.
Таблица 4 – Парные уравнения регрессии зависимости накоплений (y) от имущества случайно выбранной семьи (x).
Проанализировав показатели, мы можем видеть, что наилучший результат (максимальный коэффициент детерминации и значение F-критерия Фишера) из предложенных вариантов дает линейная модель.
Составим прогноз:
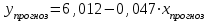
При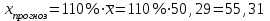
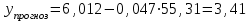
Для наглядности отобразим на графике диаграмму рассеяния, график выбранной модельной кривой (линейной) и прогнозное значение:
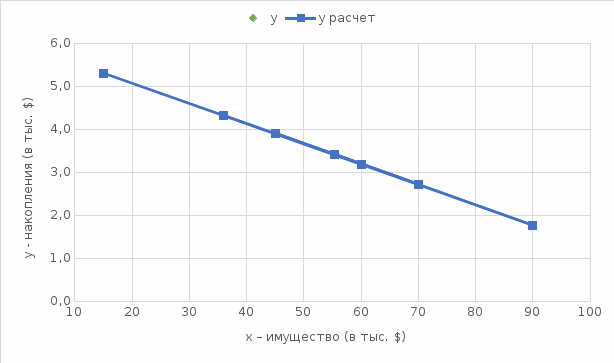
Рисунок 1 – График зависимости накоплений (y) от имущества случайно выбранной семьи (x)
Изучается зависимость показателя y от факторов х1 и х2.
Требуется (длявсехвариантов):
(вариант 1)
Составим сводную таблицу оценки зависимости производительности труда от трудоемкости продукции и удельного веса покупных изделий. Занесем данные в таблицу 5.
Таблица 5 – Оценка зависимости производительности труда (у) от трудоемкости продукции (х1) и удельного веса покупных изделий (х2)
Таким образом, найдем дисперсию:
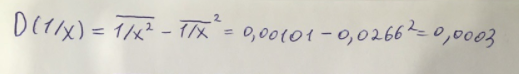
Далее выясним среднее квадратическое отклонение:
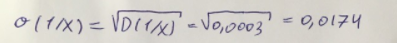
Таблица 3. – Вычисление для гиперболической модели зависимости накоплений (y) от имущества случайно выбранной семьи (x).
| № | 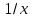 |  | 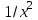 |  | 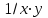 |  |  |
| 1 | 0,0167 | 3,0 | 0,00028 | 9,00 | 0,050 | 3,39 | 0,148 |
| 2 | 0,0278 | 6,0 | 0,00077 | 36,00 | 0,167 | 2,00 | 15,971 |
| 3 | 0,0278 | 5,0 | 0,00077 | 25,00 | 0,139 | 2,00 | 8,978 |
| 4 | 0,0667 | 3,5 | 0,00444 | 12,25 | 0,233 | 2,00 | 2,241 |
| 5 | 0,0111 | 1,5 | 0,00012 | 2,25 | 0,017 | 2,00 | 0,254 |
| 6 | 0,0222 | 4,5 | 0,00049 | 20,25 | 0,100 | 2,00 | 6,231 |
| 7 | 0,0143 | 2,0 | 0,00020 | 4,00 | 0,029 | 2,00 | 0,000 |
| Итого | 0,1865 | 25,5 | 0,00709 | 108,75 | 0,734 | 15,41 | 33,823 |
| Ср. знач. | 0,0266 | 3,64 | 0,00101 | 15,54 | 0,105 | 2,20 | 4,832 |
Гиперболическое уравнение парной регрессии имеет вид:
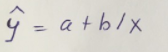
Используем метод наименьших квадратов для нахождения необходимых параметров:
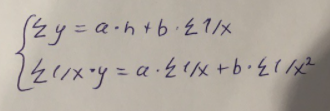
Следующим шагом найдем параметры:
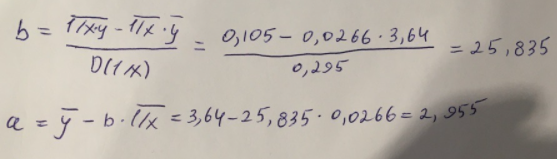
Итак, гиперболическое уравнение парной регрессии будет:
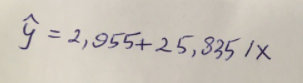
Найдем индекс корреляции для нахождения зависимости между показателями:
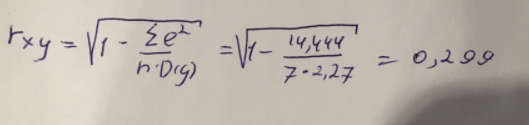
Мы видим, что значение индекса корреляции в диапазоне от 0,1 до 0,3. А значит в гиперболической модели мы можем сделать вывод о слабой зависимости между накоплениями (y) и стоимость имущества семьи (x).
Далее выполним расчет коэффициента детерминации для оценки качества модели:
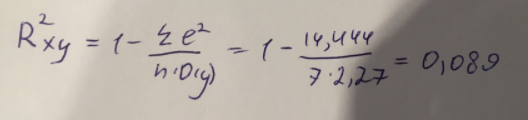
Значение коэффициента составляет 0,0,089. Также оно очень сильно отклоняется от 1. Выводом для нас будет то, что мы не видим высокого качества линейной модели уравнения регрессии. К тоже она объясняет 8,9% вариации накоплений (значений y) в зависимости от изменения стоимости имущества семьи (x).
Найдем F-критерий Фишера для определения значимости уравнения:
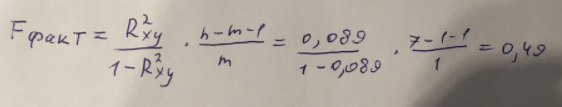
Табличное значение F-критерия мы найдем по таблице Фишера:
= 0,05 (уровень значимости); к1 = n – m – 1 = 7 – 1 – 1 = 5; к2 = m = 1.
Fтабл = 6,60
Теперь сравним фактическое и табличное значения F-критерия. Получим:
Fфакт < Fтабл (0,49 < 6,60)
Как итог, мы видим, что гиперболическое уравнение регрессии не является значимым.
Для последующего анализа и выведения итогов составим общую таблицу 4.
Таблица 4 – Парные уравнения регрессии зависимости накоплений (y) от имущества случайно выбранной семьи (x).
| Уравнение регрессии | Уравнение | Коэффициент детерминации R2 | F-критерий Фишера |
| 1. Линейное | 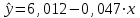 | 0,524 | 5,50 |
| 2. Экспоненциальное | 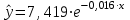 | 0,331 | 2,47 |
| 3. Гиперболическое | 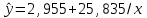 | 0,089 | 0,49 |
Проанализировав показатели, мы можем видеть, что наилучший результат (максимальный коэффициент детерминации и значение F-критерия Фишера) из предложенных вариантов дает линейная модель.
Составим прогноз:
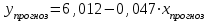
При
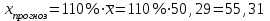
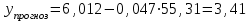
Для наглядности отобразим на графике диаграмму рассеяния, график выбранной модельной кривой (линейной) и прогнозное значение:

Рисунок 1 – График зависимости накоплений (y) от имущества случайно выбранной семьи (x)
ЗАДАЧА 2. Множественная регрессия и корреляция
Изучается зависимость показателя y от факторов х1 и х2.
Требуется (длявсехвариантов):
-
Построить линейную модель множественной регрессии. Записать стандартизованное уравнение множественной регрессии. На основе стандартизованных коэффициентов регрессии и средних коэффициентов эластичности ранжировать факторы по степени их влияния на результат. -
Найти коэффициенты парной, частной и множественной корреляции. Проанализировать их. -
С помощью F-критерия Фишера оценить статистическую надежность уравнения регрессии и коэффициента детерминации. -
С помощью частных F-критериев Фишера и t-статистики Стьюдента оценить целесообразность включения в уравнение множественной регрессии фактора х1 после х2 и фактора х2 после х1. -
По возможности составить уравнение линейной парной регрессии, оставив лишь один значащий фактор.
| y1 | 9,4 | 9,9 | 9,1 | 5,5 | 6,6 | 4,3 | 7,4 | 6,6 | 5,5 | 9,4 | 5,7 | 5,2 | 10 | 6,7 |
| x1 | 0,23 | 0,43 | 0,26 | 0,43 | 0,38 | 0,42 | 0,3 | 0,37 | 0,34 | 0,23 | 0,41 | 0,41 | 0,22 | 0,31 |
| x3 | 0,4 | 0,19 | 0,44 | 0,25 | 0,02 | 0,06 | 0,15 | 0,24 | 0,11 | 0,47 | 0,2 | 0,24 | 0,54 | 0,29 |
| y1 | Производительность труда, тыс. руб./чел. |
| x1 | Трудоемкость единицы продукции |
| x3 | Удельный вес покупных изделий |
(вариант 1)
Составим сводную таблицу оценки зависимости производительности труда от трудоемкости продукции и удельного веса покупных изделий. Занесем данные в таблицу 5.
Таблица 5 – Оценка зависимости производительности труда (у) от трудоемкости продукции (х1) и удельного веса покупных изделий (х2)
| № | х1 | х2 | у | х12 | х22 | у2 | х1∙у | х2∙у | х1∙х2 | | |
| 1 | 0,23 | 0,40 | 9,4 | 0,0529 | 0,1600 | 88,36 | 2,162 | 3,760 | 0,0920 | 8,973 | 0,182 |
| 2 | 0,43 | 0,19 | 9,9 | 0,1849 | 0,0361 | 98,01 | 4,257 | 1,881 | 0,0817 | 6,063 | 14,719 |
| 3 | 0,26 | 0,44 | 9,1 | 0,0676 | 0,1936 | 82,81 | 2,366 | 4,004 | 0,1144 | 8,929 | 0,029 |
| 4 | 0,43 | 0,25 | 5,5 | 0,1849 | 0,0625 | 30,25 | 2,365 | 1,375 | 0,1075 | 6,392 | 0,796 |
| 5 | 0,38 | 0,02 | 6,6 | 0,1444 | 0,0004 | 43,56 | 2,508 | 0,132 | 0,0076 | 5,573 | 1,056 |
| 6 | 0,42 | 0,06 | 4,3 | 0,1764 | 0,0036 | 18,49 | 1,806 | 0,258 | 0,0252 | 5,440 | 1,299 |
| 7 | 0,30 | 0,15 | 7,4 | 0,0900 | 0,0225 | 54,76 | 2,220 | 1,110 | 0,0450 | 6,988 | 0,169 |
| 8 | 0,37 | 0,24 | 6,6 | 0,1369 | 0,0576 | 43,56 | 2,442 | 1,584 | 0,0888 | 6,865 | 0,070 |
| 9 | 0,34 | 0,11 | 5,5 | 0,1156 | 0,0121 | 30,25 | 1,870 | 0,605 | 0,0374 | 6,417 | 0,842 |
| 10 | 0,23 | 0,47 | 9,4 | 0,0529 | 0,2209 | 88,36 | 2,162 | 4,418 | 0,1081 | 9,357 | 0,002 |
| 11 | 0,41 | 0,20 | 5,7 | 0,1681 | 0,0400 | 32,49 | 2,337 | 1,140 | 0,0820 | 6,294 | 0,353 |
| 12 | 0,41 | 0,24 | 5,2 | 0,1681 | 0,0576 | 27,04 | 2,132 | 1,248 | 0,0984 | 6,513 | 1,725 |
| 13 | 0,22 | 0,54 | 10,0 | 0,0484 | 0,2916 | 100,00 | 2,200 | 5,400 | 0,1188 | 9,828 | 0,030 |
| 14 | 0,31 | 0,29 | 6,7 | 0,0961 | 0,0841 | 44,89 | 2,077 | 1,943 | 0,0899 | 7,667 | 0,935 |
| Итого | 4,74 | 3,60 | 101,3 | 1,6872 | 1,2426 | 782,83 | 32,904 | 28,858 | 1,0968 | 101,300 | 22,206 |
| Среднее | 0,34 | 0,26 | 7,24 | 0,1205 | 0,0888 | 55,92 | 2,350 | 2,061 | 0,0783 | 7,236 | 1,586 |