Файл: 1 Классификация и физический механизм работы вч и свч генераторов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 905
Скачиваний: 1
СОДЕРЖАНИЕ
Узкополосные согласующие цепи связи
Возбудители косвенного синтеза
Однополосная модуляция. Балансные модуляторы. Фильтры в однополосной аппаратуре.
Аналитическое сравнение ФМ и ЧМ.
Фазовая модуляция. Способы осуществления
Сигналы ЧМн формируются в возбудителе при скоростях передачи не более 1000 Бод.
Квадратурное представление сигнала
Радиоприемные и радиопередающие устройства
Раздел 1. Ведение. Принципы работы и классификация рПрУ
Принцип построения приемника прямого усиления
Принцип построения супергетеродинного приемника
Проблема дополнительных каналов приема в супергетеродине
Приемники прямого преобразования (с преобразованием на нулевую пч)
Приемники с цифровой обработкой сигнала
Пример. Радиовещательный приемник св диапазона
Пример. Приемник мобильной станции gsm 900
Ключевые режимы генератора с внешним возбуждением
Варакторные умножители частоты
Общие принципы построения схем
Схемы анодной цепи генератора.
Схемы питания цепей накала мощных генераторных ламп
Схема генератора с общей сеткой
Совместная работа генераторных ламп на общую нагрузку
Схемы широкодиапазонных генераторов
Схемы узкополосных генераторов
Синфазные мостовые схемы сложения мощностей
Амплитудные условия в автогенераторе
Стабильность частоты автогенератора
Схемы автогенераторов с колебательными контурами
Схемы кварцевых автогенераторов
Компенсационный метод синтеза частот
Применение автоподстройки частоты в
Устойчивость работы генератора с внешним возбуждением
Паразитные колебания в генераторе
Общие сведения об амплитудной модуляции
Коллекторная амплитудная модуляция
Усиление модулированных колебаний
Общие сведения об однополосной модуляции
Способ многократной балансной модуляции
Общие сведения об угловой модуляции
Спектр сигнала с угловой модуляцией
Рисунок 8.5 – 4-х канальная однополосная модуляция
На этом рисунке ВУ – входное устройство, которое ограничивает полосу
и динамический диапазон информационного сигнала, а также обеспечивает согласование линии с балансным модулятором. Кроме того, во входном устройстве имеется усилитель и аттенюатор;
АТТ – аттенюатор, регулирующий уровень пилот-сигнала;
Σ – сумматор.
Выбор частот и размещение каналов на выходе устройства иллюстрируется рисунком 8.6. При использовании стандартного телефонного канала с полосой 250 ÷ 3000Гц, поднесущие частоты f1 , f2 , f3 выбираются с интервалом 3000 Гц. Каналы, расположенные рядом с f1 , обозначаются А1 и В1 . Остальные соответственно А2 и В2. Многоканальный (групповой) сигнал на выходе сумматора поступает на усилитель, назначение которого - компенсация затухания сигналов в балансных модуляторах и фильтрах. Для переноса группового сигнала на рабочую частоту используется повторное балансное преобразование.
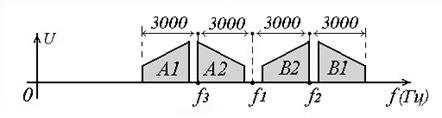
Рисунок 8.6 – Спектр группового сигнала
Каждый канал группового сигнала может быть дополнительно уплотнён несколькими узкополосными каналами, несущими информацию в цифровой форме.
Общие сведения об угловой модуляции
⇐ Предыдущая38394041424344454647Следующая ⇒
| |
Яндекс.Директ |
u(t)=Ucos(ωt+φ)= UcosФ(t) (9.1)
Очевидно, что в соответствии с передаваемой информацией, помимо амплитуды, можно менять частоту ω или фазу φ, осуществляя, таким образом, частотную или фазовую модуляцию (ЧМ, ФМ). Согласно (9.1) в обоих случаях будет меняться угловой аргумент косинуса Ф(t), поэтому частотную и фазовую модуляцию объединяют общим термином «угловая модуляция». Тем не менее, как будет показано ниже, между ЧМ и ФМ есть и существенные различия.
Воспользуемся простейшей моделью информационного сигнала в форме (7.1). Тогда колебание с частотной модуляцией можно представить в следующем виде
u(t)=Ucos[(ω+ΔωcosΩt)t+φо] (9.2)
В этом выражении Δω – амплитуда отклонения частоты при ЧМ, получившая название – девиация частоты; φо – произвольная постоянная, соответствующая фазовому сдвигу при t = 0. Согласно (7.1) и (9.1)
Δω=Кчм·UΩ (9.3)
Здесь Кчм - крутизна характеристики частотного модулятора.
Аналогично для фазовой модуляции получим
u(t)=Ucos(ωt+ΨcosΩt+φο) (9.4)
В этом выражении Ψ – амплитуда отклонения фазы, названная индексом модуляции. По аналогии с (9.3)
Ψ=Кфм·UΩ (9.5)
Где Кфм - крутизна характеристики фазового модулятора.
Частота и фаза гармонического колебания связаны следующими соотношениями
Используя эти зависимости можно определить связь между ЧМ и ФМ.
Подставив значение Ф(t) из (9.4) в (9.6), определим как изменяется частота при ФМ
Сравнивая частоту в выражениях (9.2) и (9.8), с учётом (9.5), получим
Δω(ФМ) = ΨΩ = Ω·Кфм·UΩ (9.9)
Таким образом, девиация частоты при ФМ пропорциональна амплитуде информационного сигнала и его частоте, в отличие от (9.3). Поэтому, в информационном сигнале, переданном фазовой модуляцией и принятым частотным детектором, произойдёт подъём верхних частот (исказится амплитудно-частотная характеристика).
Подставим теперь частоту из (9.2) в (9.7) и определим как меняется фаза при ЧМ .
Сравнивая фазу в (9.4) с (9.10), с учётом (9.3), получим
В этом случае, индекс модуляции при ЧМ пропорционален амплитуде информационного сигнала и обратно пропорционален его частоте, в отличие от (9.5). Поэтому, в информационном сигнале, переданном частотной модуляцией и принятом фазовым детектором, произойдёт завал верхних частот.
Рассмотренные отличия проявляются только в случае реальных информационных сигналов с меняющейся частотой
Ω. Для его модели (7.1) с постоянной частотой, различие между ЧМ и ФМ полностью отсутствует.
На основании (9.9) и (9.11) возможно взаимное преобразование ЧМ в ФМ и наоборот, обеспечив необходимую зависимость (или независимость) индекса модуляции от частоты модулирующего сигнала.
В частности, для преобразования ФМ в ЧМ, необходимо амплитуду модулирующего сигнала изменять обратно пропорционально его частоте. Это может быть выполнено с помощью интегрирующей RC цепи, через которую перед модуляцией должен быть пропущен модулирующий сигнал (см. рисунок 9.1а).
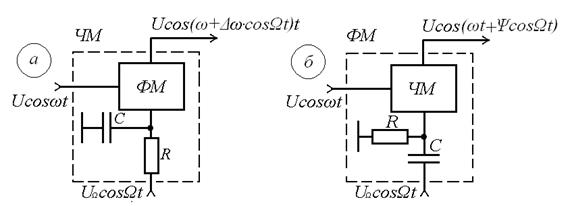
Рисунок 9.1 – Преобразование видов угловой модуляции
Действительно, коэффициент передачи такой цепи
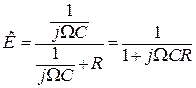 . При условии R>>ΩмаксС
. При условии R>>ΩмаксС(9.12)
Аналогично при использовании дифференцирующей цепи на входе частотного модулятора можно получить фазовую модуляцию (см. рисунок 9.1б).
Спектр сигнала с угловой модуляцией
⇐ Предыдущая39404142434445464748Следующая ⇒
| | |
Здесь Jn(Ψ) – функция Бесселя первого рода n – го порядка, аргументом которой является индекс модуляции Ψ.
Согласно (9.13), спектр сигнала с угловой модуляцией теоретически бесконечен . Форма огибающей спектра определяется зависимостью функций Бесселя от индекса модуляции. Графики первых четырёх функций Бесселя представлены на рисунке 9.2. Особенностью этих функций является затухающий колебательный характер, поэтому при некоторых значениях Ψ, указанных на рисунке 9.2, несущая частота (Jo) исчезает. В связи с этим, термин «несущая», при рассмотрении угловой модуляции, заменяют термином «средняя частота». Первый максимум функций Бесселя, начиная с n=1 , соответствует Ψ=n+1.
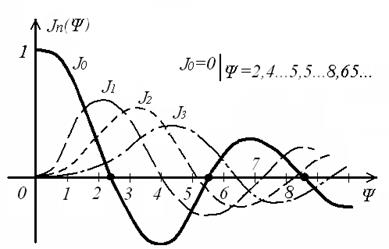
Рисунок 9.1 – Функции Бесселя
Затухающий характер функций Бесселя позволяет на практике без последствий ограничивать полосу занимаемых частот на уровне составляющих, амплитуда которых не превышает 1% от немодулированной несущей.
Эффективную полосу сигнала с угловой модуляцией в этом случае определяют эмпирической формулой
В последнем выражении Fмакс – максимальная частота модулирующего сигнала.
На рисунке 9.3 в качестве примера представлены спектры для некоторых значений Ψ [9].
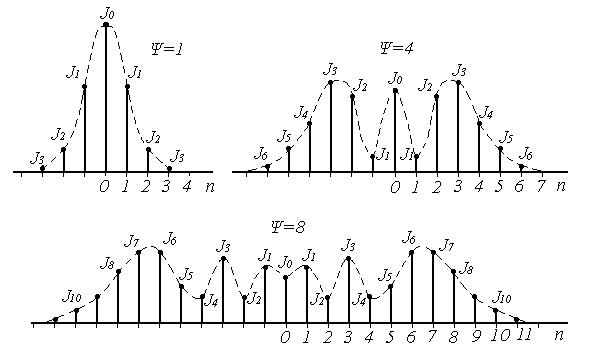
Рисунок 9.3 – Спектры сигналов с угловой модуляцией.
Как уже отмечалось выше, при угловой модуляции одним гармоническим тоном, различия между ФМ и ЧМ нет, т.к индекс модуляции в этом случае величина постоянная. Иначе обстоит дело при модуляции сложным многочастотным сигналом. Поясним это на следующем примере. Пусть фазовая модуляция осуществляется двух тоновым сигналом, в котором одна частота (