Файл: Контур регулирования уровня металла в промежуточном ковше мнлз.docx

2.1 Расчет статической характеристики объекта управления методом наименьших квадратов

Для предварительного теоретического исследования функционирования системы автоматического управления необходимо иметь математическое описание статической характеристики оптимизируемого реального процесса. Исходной информацией для математического описания статической характеристики автоматизируемого процесса являются полученные экспериментальные данные об установившихся значениях выходного параметра процесса при фиксированных значениях входного параметра[6].

Для математического описания статических характеристик используются полученные с применением методов математической статистики регрессионные уравнения вида Y = f(X), определяющие функциональную связь между выходным Y и входным X параметрами оптимизируемого процесса. Запас функций, которыми можно математически выразить зависимость Y = f(X), разнообразен. Предпочтение обычно отдается многочленам (полиномам) целых положительных степеней вида:



Так как статическая характеристика нелинейна, то для получения уравнения (теоретической линии регрессии) статической характеристики целесообразно использовать полином третьей степени вида:



При определении постоянных коэффициентов a, b, c, d аппроксимирующего полинома используется наиболее универсальный и наиболее часто применяемый в инженерной практике метод наименьших квадратов:



где n – число экспериментальных пар данных,

– экспериментальное значение выходного параметра при значении входного Xi,

– теоретическое значение выходного параметра при значении входного Xi.

Коэффициенты полинома определяются из решения системы уравнений

---

, полученных с использованием метода наименьших квадратов:
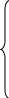 y_i = na + b  x_i + c  x_i² + d  x_i³ + e  x_i⁴ ;

x_iy_i = a  x_i + b  x_i² + c  x_i³ + d  x_i⁴ + e  x_i⁵ ;

 x_i²y_i = a  x_i² + b  x_i³ + c  x_i⁴ + d  x_i⁵ + e x_i⁶ ;

 x_i³y_i = a  x_i³ + b  x_i⁴ + c  x_i⁵ + d  x_i⁶ + e x_i⁷ ;

 x_i⁴y_i = a  x_i⁴ + b  x_i⁵ + c  x_i⁶ + d  x_i⁷ + e x_i⁸ ;

Расчет коэффициентов уравнения статической характеристики методом наименьших квадратов приведен в таблице 2.

Таблица 1 - Расчет коэффициентов уравнения статической характеристики





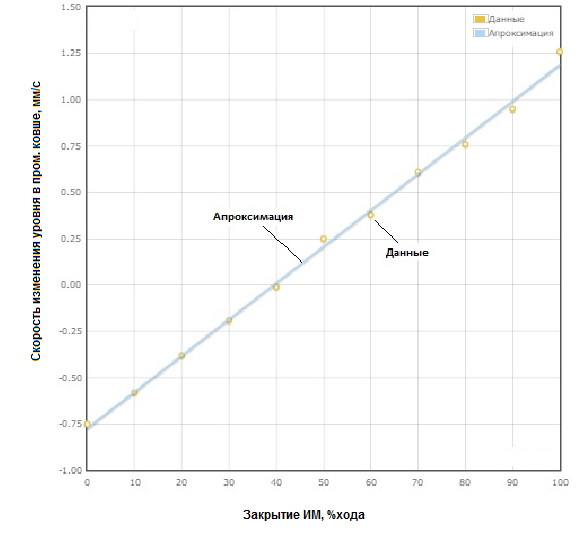
Рисунок 2.1. Апроксимация статической характеристики объекта
Аппроксимирующий полином примет вид:

Y=-0.78*x+0.019

2.2 Расчет динамических параметров по экспериментальной кривой разгона объекта

Наиболее сложными для управления являются объекты астатического типа или объекты без самовыравнивания. Отличительной чертой таких объектов является наличие интегрирующего элемента, определяющего их специфические динамические свойства.

Выходная величина объекта без самовыравнивания после нанесения входного одно- кратного скачкообразного возмущения неограниченно изменяется с постоянной скоростью, пропорциональной величине входного возмущающего воздействия.

Увеличение объема металла поступающего в промежуточный ковш



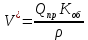
Где – плотность жидкого металла =7860 кг/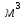

---

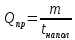
Где m – масса жидкого металла при заданном уровне металла (700 мм),

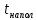– время наполнения промковша при 100% открытом ИМ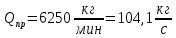





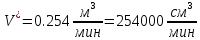
Внутреннее сечение промежуточного ковша Sи скорость изменения уровня жидкого металла в промковше



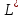
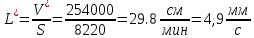
Расчет траектории изменения информационного сигнала вторичного прибора производится с помощью численного метода Эйлера по формулам:





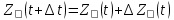
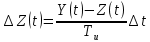
Результаты расчета представлены в таблице 3. По методу Элера определяются координаты других точек траектории Z(t). Расчет необходимо производить до достижения постоянной скорости приращения ΔZ, что было достигнуто 50 м шаге расчета ΔZ(t=50)=4.87, что практически совпадает со скоростью изменения уровня в промковше L*=4,9.

Таблица 2 - Расчет траектории выходного информационного сигнала

t	Y(t)	Z(t)	delZ(t)
1	4,9	0	0,49
2	9,8	0,49	0,931
3	14,7	1,421	1,3279
4	19,6	2,7489	1,68511
5	24,5	4,43401	2,006599
6	29,4	6,440609	2,295939
7	34,3	8,736548	2,556345
8	39,2	11,29289	2,790711
9	44,1	14,0836	3,00164
10	49	17,08524	3,191476
11	53,9	20,27672	3,362328
12	58,8	23,63905	3,516095
13	63,7	27,15514	3,654486
14	68,6	30,80963	3,779037
15	73,5	34,58867	3,891133
16	78,4	38,4798	3,99202
17	83,3	42,47182	4,082818
18	88,2	46,55464	4,164536
19	93,1	50,71917	4,238083
20	98	54,95726	4,304274
21	102,9	59,26153	4,363847
22	107,8	63,62538	4,417462
23	112,7	68,04284	4,465716
24	117,6	72,50856	4,509144
25	122,5	77,0177	4,54823
26	127,4	81,56593	4,583407
27	132,3	86,14934	4,615066
28	137,2	90,7644	4,64356
29	142,1	95,40796	4,669204
30	147	100,0772	4,692283
31	151,9	104,7695	4,713055
32	156,8	109,4825	4,731749
33	161,7	114,2143	4,748575
34	166,6	118,9628	4,763717
35	171,5	123,7265	4,777345
36	176,4	128,5039	4,789611
37	181,3	133,2935	4,80065
38	186,2	138,0942	4,810585
39	191,1	142,9047	4,819526
40	196	147,7243	4,827574
41	200,9	152,5518	4,834816
42	205,8	157,3867	4,841335
43	210,7	162,228	4,847201
44	215,6	167,0752	4,852481
45	220,5	171,9277	4,857233
46	225,4	176,7849	4,86151
47	230,3	181,6464	4,865359
48	235,2	186,5118	4,868823
49	240,1	191,3806	4,871941
50	245	196,2525	4,874747

---

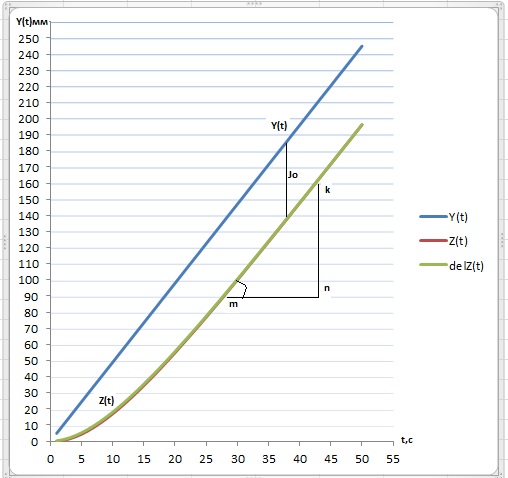
Рисунок 2.1 - Расчетные траектории изменения уровня металла

Полученная расчетная траектория является искомой траекторией кривой разгона астатического объекта второго порядка.

По графику рис. определяются:

величина интеграла 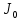=2.22 мм – динамическая ошибка измерительного канала;

тангенс угла tgα = KN/MN = 1,206 и угол α=50.33°

Определим коэффициенты дифференциального уравнения астатического объекта





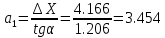
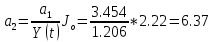
Составим уравнение динамики ОУ



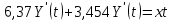
Точное решение уравнение имеет вид

---

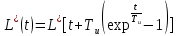
3 СТРУКТУРНАЯ СХЕМА САУ РЕГУЛИРОВАНИЯ УРОВНЯ ЖИДКОГО МЕТАЛЛА В ПРОМЕЖУТОЧНОМ КОВШЕ

Любой контур управления в обязательном порядке содержит объект управления, регулятор и механизм воздействия на управляемый объект. Заданием на курсовой проект был определен объект управления – интегральное звено и инерционное звено первого порядка.


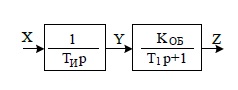
Рисунок 3.1 - Объект управления

Передаточная функция такого объекта описывается уравнением вида

,

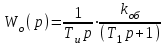Т_о – постоянная времени объекта, с;

τ – время запаздывания, c;

В качестве регулятора для данного типа объекта выбираем пропорционально-интегральный регулятор (ПИ-регулятор), передаточная функция которого описывается уравнением вида:



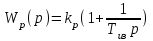
где k_р – коэффициент передачи регулятора;

Т_из – время изодрома.

Заданием определен исполнительный механизм постоянной скорости типа МЭО 100/63-0,25, описываемый передаточной функцией вида: 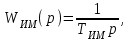где Т_им – время полного хода, или время перекладки исполнительного механизма от одного концевого выключателя до другого. Т_им является настроечным параметром контура управления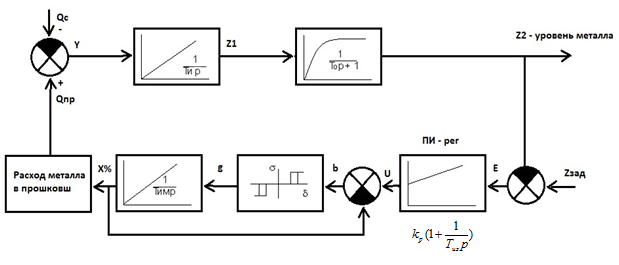



Рисунок 3.2 - Структурная схема контура управления.

Объект управления, представляющий из себяинтегрирующее звено, инерционное звено первого порядка с запаздыванием, представлен в. Первое звено с постоянной времени, равной постоянной времени объекта, второе звено – с постоянной времени, равной времени запаздывания (в первом приближении звено запаздывания можно заменить инерционным звеном первого порядка).

---