Файл: Контур регулирования уровня металла в промежуточном ковше мнлз.docx

Сигнал с выхода объекта Z₂ сравнивается с сигналом задания Z_з. Разница ε=Z_з-Z₂ поступает на вход ПИ-регулятора. ПИ-регулятор отрабатывает сигнал рассогласования ɛ во времени, выставляя на выходе управляющее воздействие U, которое, после вычитания сигнала обратной связи, подается на вход релейного элемента. Наиболее правильно в качестве сигнала обратной связи по положению ИМ использовать сигнал КиТ. При значительных сигналах рассогласования и при начальном положении ИМ близким к нулевому (до 15%хода), можно при формировании сигнала ООС по положению ИМ использовать выражение Хн+КиТ .В проекте применялся первый вариант формирования отрицательной обратной связи (КиТ).

Релейный элемент представляет собой трехпозиционное реле, которое переключается в зависимости от уровня сигнала ошибки, зоны нечувствительности ∆Z_нч, являющейся настроечным параметром системы управления, а также значения переключающей функции в предыдущий момент времени. Варианты формирования значения переключающей функции на последующем шаге в зависимости от значения этой функции на предыдущем шаге представлены на рис. Зона нечувствительности релейного элемента ограничивает частоту перемещений исполнительного механизма, ухудшая при этом качество регулирования.



Рисунок 3.3 - Варианты формирования значения переключающей функции на последующем шаге в зависимости от значения этой функции на предыдущем шаге.
В зависимости от сигнала на выходе реле исполнительный механизм:

а) работает на увеличение выходной величины если σ=+1;

б) неподвижен если σ=0;

в) работает на уменьшение выходной величины если σ=-1.

Исполнительный механизм рассматривается как интегрирующее звено, причем скорость исполнительного механизма обратно пропорциональна его постоянной времени:



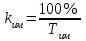
Изменение средней скорости исполнительного механизма (уменьшение от максимально возможной) осуществляется с помощью импульсного коммутирующего устройства ИКУ. При программировании работы ИКУ необходимо учитывать следующие рекомендации:

1. 
   Продолжительность работы цикла расчета управляющего воздействия зависит от инерционных свойств объекта и не должна превышать 1-5с.
   
2. 
   При выборе продолжительности цикла расчета 1с. минимальное значение скорости ИМ не должно быть меньше 0,1Ким _max.
   
3. 
   Минимально возможная продолжительность включения ИМ в пределах одного цикла расчета зависит от конструктивных особенностей ИМ и не должна быть меньше 0,1-0,15 с.
   

---

---

3.1 Расчет настроек контура управления.

Существует большое количество методик расчета оптимальных настроек регулятора в одноконтурных системах, метод симметричным оптимумом (СО) заключается в компенсации инерционных свойств объекта. Который обеспечивает малое время переходного процесса и перерегулирование, а также не требует большого объема расчетов.

При использовании метода “СО” значения настроечных параметров ПИ-регулятора определяются по следующим формулам:



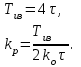
С учетом этого имеем:

Т_из = 4τ = 40с;

К_р = Т_из / 2К_об = 40/(2*0,32*10)=6,25

Зона нечувствительности релейного элемента и зона гистерезиса также являются настроечными параметрами контура управления. Он влияют на качество регулирования, т. е. то, насколько близко регулируемая величина будет подходить к заданному значению, и на частоту срабатывания ИМ. Точность регулирования возрастает с уменьшением величины зоны нечувствительности, однако при этом также растет частота колебаний исполнительного механизма, что нежелательно вследствие быстрого износа вращающихся частей. Кроме того, уменьшение зоны нечувствительности ограничено наличием погрешности измеряющего прибора.

Время полного хода исполнительного механизма напрямую влияет на качество переходного процесса. Чем меньше время полного хода, тем больше скорость работы исполнительного механизма, а, следовательно, тем быстрее система в целом выходит на новое заданное значение.

С уменьшением скорости исполнительного механизма возрастает перерегулирование, что не всегда допустимо на реальных объектах, в особенности нагревательных печах, связанных со строгим соблюдением технологических условий температурного режима. Также, в свою очередь, повышение скорости исполнительного механизма приводит к увеличению амплитуды колебаний вала исполнительного механизма, что вместе с зоной нечувствительности определяет срок службы последнего, и как следствие – рентабельность внедрения данной системы на производство.

---

3.2 Расчет траектории переходного процесса

Расчет траектории переходного процесса основан на применении численного метода Эйлера, позволяющего рассчитать траекторию изменения выходного сигнала на выходе инерционного звена при любом изменении входного сигнала. Основой метода является дифференциальное уравнение звена первого порядка:

,

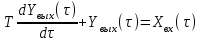или



Зная структурную схему контура управления можно последовательно рассчитать переходный процесс задания из одного установившегося состояния системы в другое на выходе объекта управления, при изменении задания в данном конкретном случае ступенчато на величину .

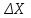4 РАСЧЕТ ПЕРЕХОДНОГО ПРОЦЕССА В КОНТУРЕ УПРАВЛЕНИЯ

Расчет переходного процесса вручную проводился для первых десяти точек траектории с шагом ∆t=0.5с, с динамическими параметрами настройки, рассчитанными в пункте 3.1 в целях проверки результатов машинного расчета, четкого понимания метода Эйлера и принципов работы контура цифрового управления.



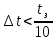
Введём следующие обозначения:

τ -текущее время, с;

Х-входная величина ИМ;

Х_н-начальное положение вала ИМ, %хода ИМ;

Y-установившееся значение регулируемой величины в соответствии со статической характеристикой, V;

Z-выходная величина, V;

Е-величина рассогласования (E=Z_зад-Z);

F-величина интеграла рассогласования (F=Edt);

U-управляющее воздействие, формируемое ПИ-регулятором, %хода ИМ;

σ-сигнум функция релейного элемента регулирующего устройства;

∆Z1/∆τ,∆Z2/∆τ-производные, мм/с;

₁-величина зоны нечувствительности релейного элемента, %хода ИМ;

₂-величина зоны гистерезиса релейного элемента, %хода ИМ;
t=0:

X=X_н=0 %хода ИМ:

Y=Y_н=Z1=Z2=0;

F=0;

Z_зад=40 мм;

Е=Z_зад-Z2_o=100-0=100 мм;

F=F_н+ 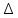tE=0+50=50 ;

U=k_р(E+F/T_и)=6,25(100+50/40)=632,8;

Если U<-1,то σ=-1, если U>+1, тоσ=+1, в противном случае σ=0.

σ(τ=0)=+1
t=0.5:

X=X_н+σk_имτ=50+0,51,59 =50,79%хода ИМ;

Y=-0,78*50,79+0,019= 38,981;

Z1=Z1_пр+∆Z1/∆τ=0+0=0;

---

Z2=Z2_пр+∆Z2/∆τ=0;

∆Z1/∆τ=(Y-Z1)/T_o=(-38,98-0)/10=-3,89;

∆Z2/∆τ=(Z1-Z2)/τ_з=(0-0)/6=0 ;

Е=Zзад-Z2=100-0=100мм;

F=F_н+∆τE=0+50=50;

U=k_р(E+F/T_и)=6,25(100+50/40)= 632,8 ;

Если U<-1,то σ=-1, если U>+1, тоσ=+1, в противном случае σ=0.

σ(τ=0)=+1
t=1:

X=X_н+σk_имτ=50+11,59 =51,79%хода ИМ;

Y=-0,78*51,79+0,019= -40,37;

Z1=Z1_пр+∆Z1/∆τ=0+(-3,89)=-3,89;

Z2=Z2_пр+∆Z2/∆τ=0;

∆Z1/∆τ=(Y-Z1)/T_o=(-40,37-(-3,89))/10=-4,42;

∆Z2/∆τ=(Z1-Z2)/τ_з=(-3,89-0)/6=-0,64 ;

Е=Zзад-Z2=100-0=100мм;

F=F_н+∆τE=0+50=50;

U=k_р(E+F/T_и)=6,25(100+50/40)= 632,8 ;

Если U<-1,то σ=-1, если U>+1, тоσ=+1, в противном случае σ=0.

σ(τ=0)=+1
t=1,5:

X=X_н+σk_имτ=50+1,51,59 =52,38 %хода ИМ;

Y=-0,78*52,38+0,019= -40,83;

Z1=Z1_пр+∆Z1/∆τ=-3,89+(-4,42)=-8,31;

Z2=Z2_пр+∆Z2/∆τ=0+(-0,64)=-0,64;

∆Z1/∆τ=(Y-Z1)/T_o=(-40,83-(-8,31))/10=-3,25;

∆Z2/∆τ=(Z1-Z2)/τ_з=(-8,31-(-0,64))/6=-1,27;

Е=Zзад-Z2=100-0,64=99,36мм;

F=F_н+∆τE=49,68;

U=k_р(E+F/T_и)=6,25(99,36+49,68/40)=653,3 ;

Если U<-1,то σ=-1, если U>+1, тоσ=+1, в противном случае σ=0.

σ(τ=0)=+1
t=2:

X=X_н+σk_имτ=50+21,59 =53,18%хода ИМ;

Y=-0,78*53,18 +0,019= -41,46;

Z1=Z1_пр+∆Z1/∆τ=-8,31+(-3,25)=-11,56;

Z2=Z2_пр+∆Z2/∆τ=-0,64+(-1,28)=-1,92;

∆Z1/∆τ=(Y-Z1)/T_o=(-41,46-(-11,56))/10=-2,9;

∆Z2/∆τ=(Z1-Z2)/τ_з=(-11,56-(-1,92))/6=-1,6;

Е=Zзад-Z2=100-1,92=98,08мм;

F=F_н+∆τE=49,04;

U=k_р(E+F/T_и)=6,25(98,08+49,04/40)=649,6 ;

Если U<-1,то σ=-1, если U>+1, тоσ=+1, в противном случае σ=0.

σ(τ=0)=+1
t=2,5:

X=X_н+σk_имτ=50+2,51,59 =53,97%хода ИМ;

Y=-0,78*53,97 +0,019= -42,07;

Z1=Z1_пр+∆Z1/∆τ=-11,56+(-2,9;)=-14,46;

Z2=Z2_пр+∆Z2/∆τ=-1,92+(-1,6)=-3,52;

∆Z1/∆τ=(Y-Z1)/T_o=(-42,07-(-14,46;))/10=-2,7;

∆Z2/∆τ=(Z1-Z2)/τ_з=(-14,46-(-3,52))/6=-1,82;

Е=Zзад-Z2=100-3,52=96,48мм;

F=F_н+∆τE=49,24;

U=k_р(E+F/T_и)=6,25(96,48+49,24/40)=645,7 ;

Если U<-1,то σ=-1, если U>+1, тоσ=+1, в противном случае σ=0.
t=3:

X=X_н+σk_имτ=50+31,59 =54,77 %хода ИМ;

Y=-0,78*54,77+0,019= -42,7;

Z1=Z1_пр+∆Z1/∆τ=-14,46+(-2,7;)=-17,16;

Z2=Z2_пр+∆Z2/∆τ=-3,52+(-1,82)=-5,34;

∆Z1/∆τ=(Y-Z1)/T_o=(-42,7-(-17,16;))/10=-2,5;

∆Z2/∆τ=(Z1-Z2)/τ_з=(-17,16-(-5,34))/6=-1,97;

Е=Zзад-Z2=100-5,34=94,66 мм;

F=F_н+∆τE=347,33;

U=k_р(E+F/T_и)=6,25(94,66+47,33/40)=640,81 ;

Если U<-1,то σ=-1, если U>+1, тоσ=+1, в противном случае σ=0.

σ(τ=0)=+1

t=3,5:

X=X_н+σk_имτ=50+3,51,59 =55,56%хода ИМ;

Y=-0,78*55,56 +0,019= -43,31;

Z1=Z1_пр+∆Z1/∆τ=-17,16+(-2,5;)=-19,66;

Z2=Z2_пр+∆Z2/∆τ=-5,34+(-1,97)=-7,31;

∆Z1/∆τ=(Y-Z1)/T_o=(-43,31-(-19,66;))/10=-2,3;

∆Z2/∆τ=(Z1-Z2)/τ_з=(-19,66-(-7,31))/6=-2,05;

Е=Zзад-Z2=100-7,31=692,69мм;

F=F_н+∆τE=46,34;

U=k_р(E+F/T_и)=6,25(92,69+46,34/40)=635,62 ;

Если U<-1,то σ=-1, если U>+1, тоσ=+1, в противном случае σ=0.

σ(τ=0)=+1
t=4:

X=X_н+σk_имτ=50+41,59 =56,36%хода ИМ;

Y=-0,78*56,36 +0,019= -43,94;

Z1=Z1_пр

---