ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 439
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1. ИНТЕРФЕРЕНЦИЯ СВЕТА
Основные формулы и законы
• Скорость света в среде
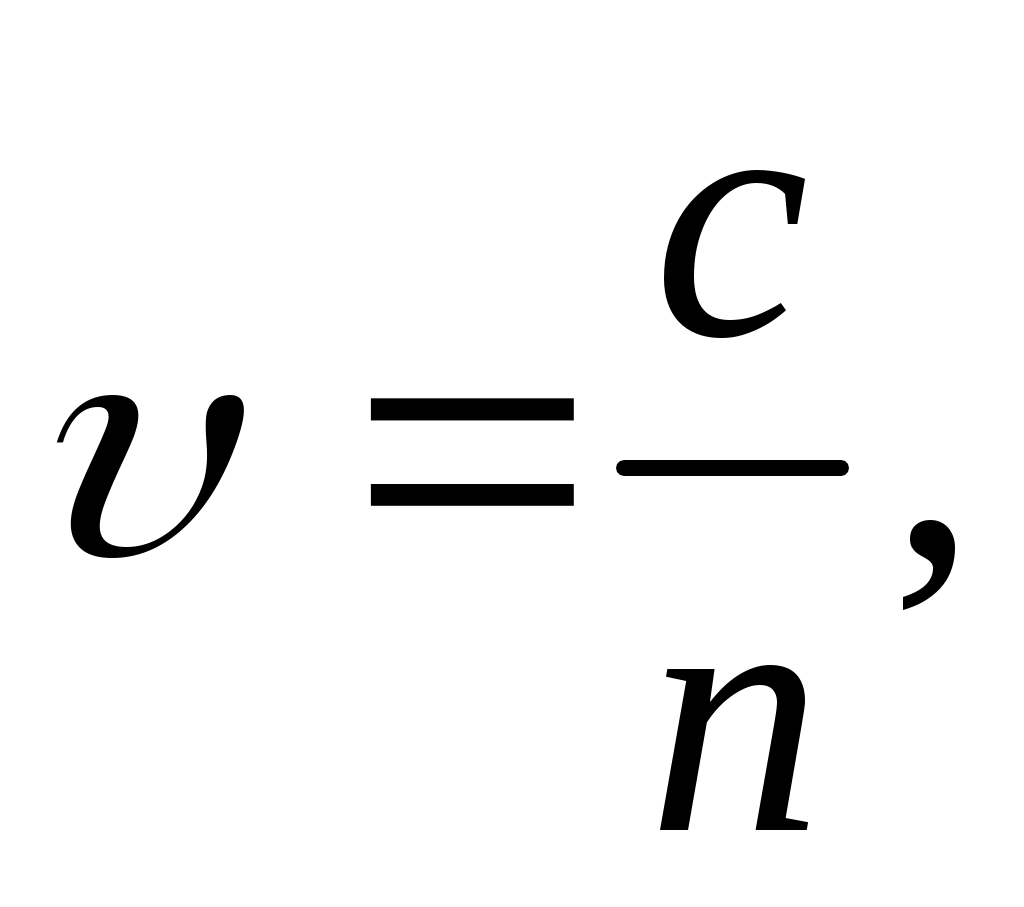
где 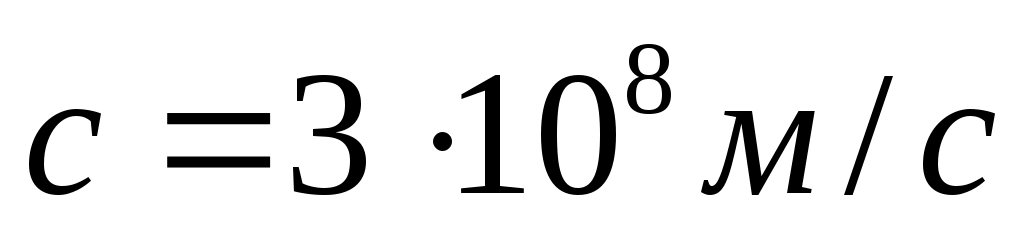 – скорость света в вакууме; n- абсолютный показатель преломления среды.
– скорость света в вакууме; n- абсолютный показатель преломления среды.
• Оптическая длина пути световой волны
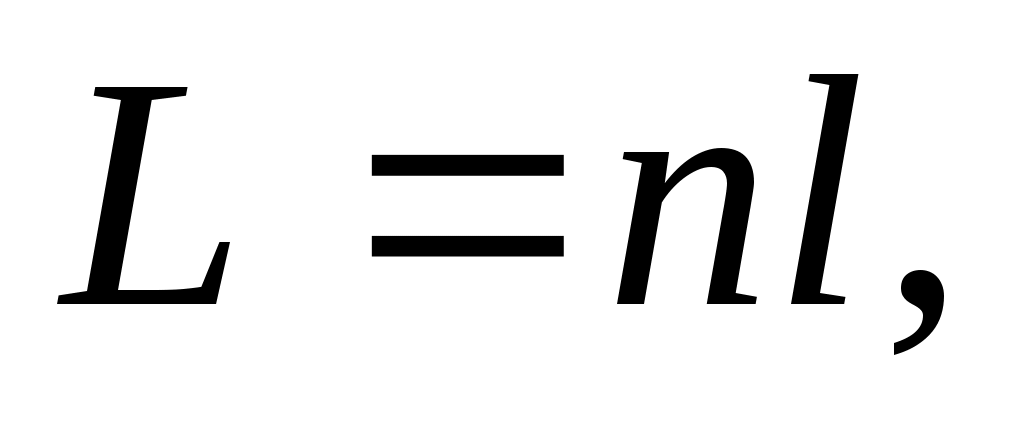
где 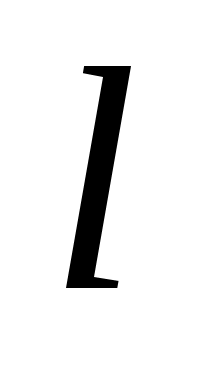 – геометрическая длина пути световой волны в среде с показателем преломления n.
– геометрическая длина пути световой волны в среде с показателем преломления n.
• Оптическая разность хода двух световых волн
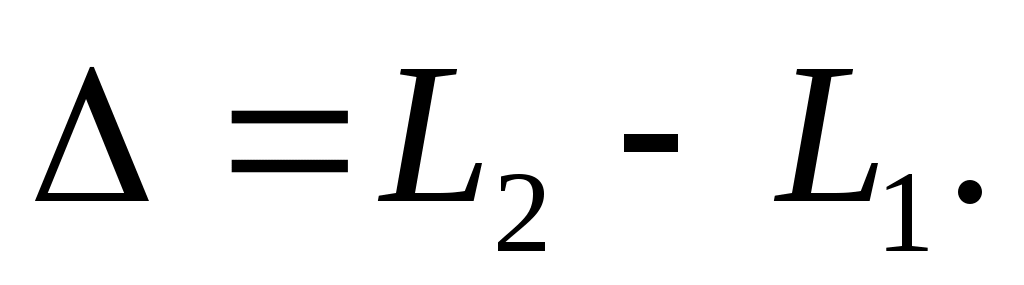
• Зависимость разности фаз от оптической разности хода световых волн


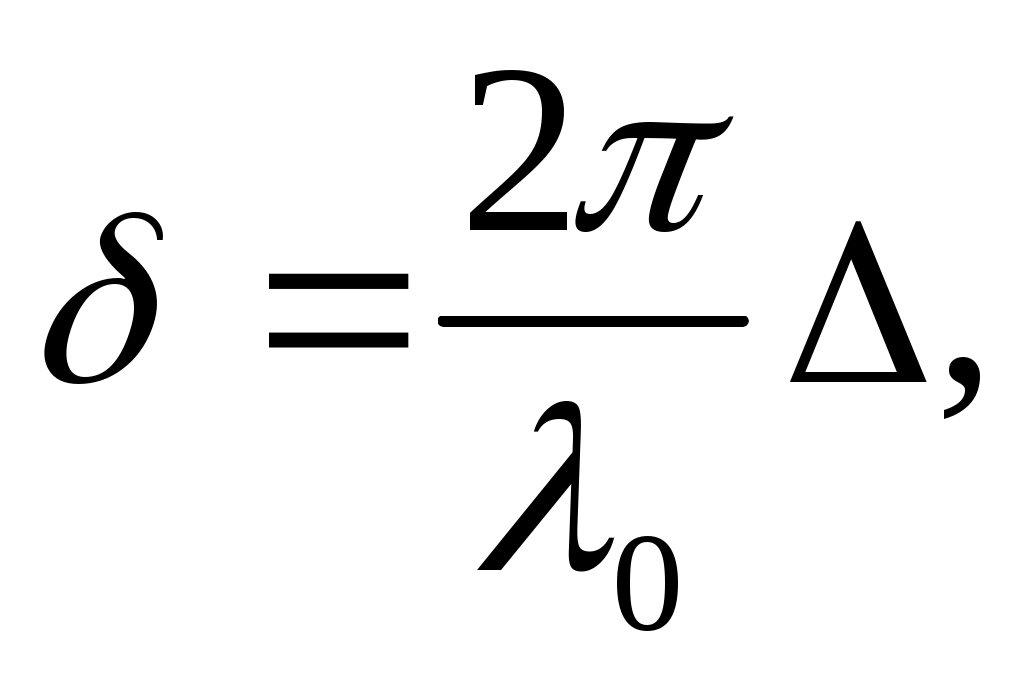
где λ0 – длина световой волны в вакууме.
• Условие интерференционных максимумов
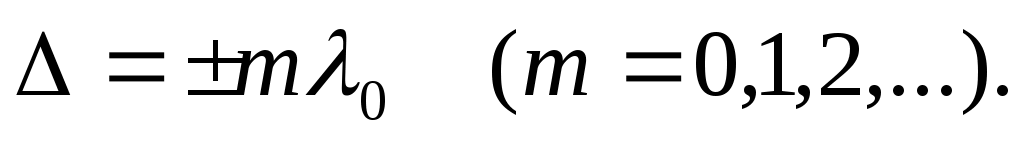
• Условие интерференционных минимумов
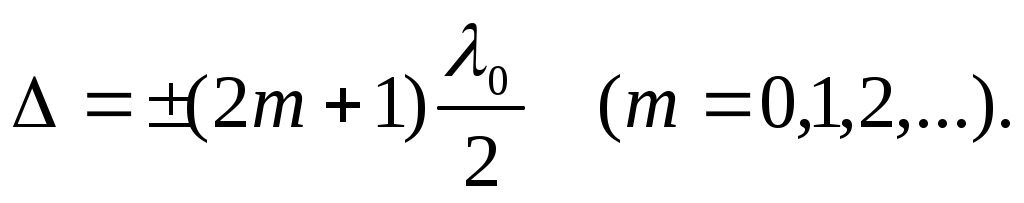
-
Координаты максимумов и минимумов интенсивности в опыте Юнга
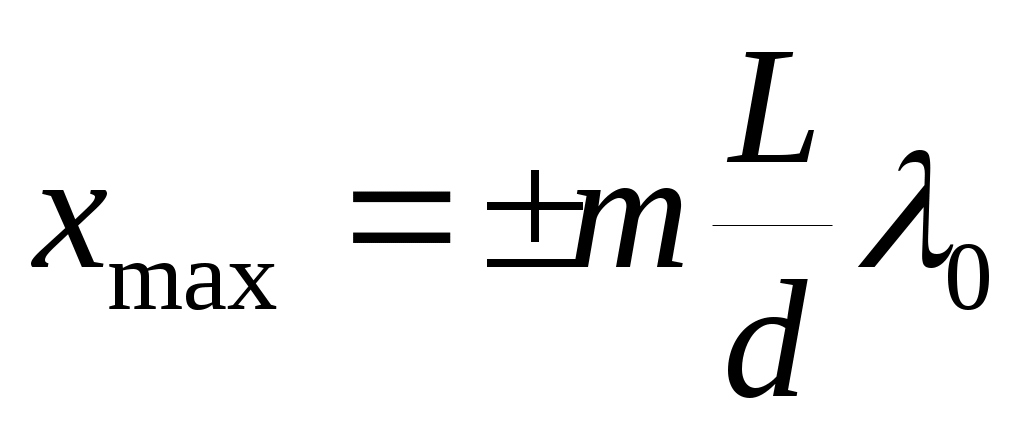 ;
; 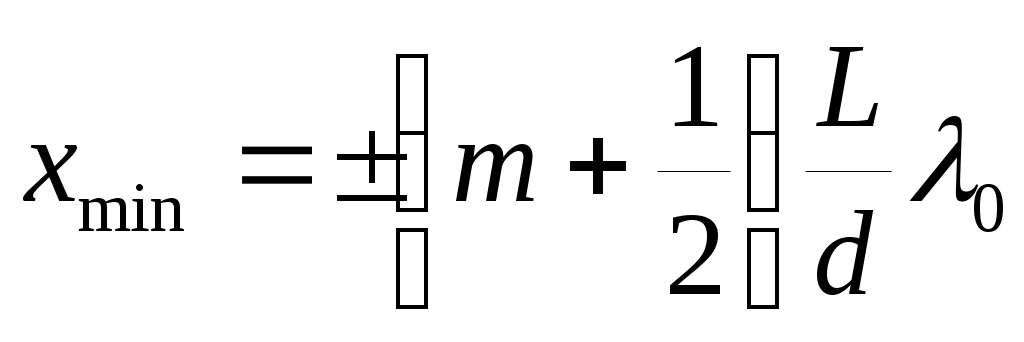 ,
,
где m= 0, 1, 2…-номер интерференционной полосы, d – расстояние между двумя когерентными источниками, находящимися на расстоянии L от экрана 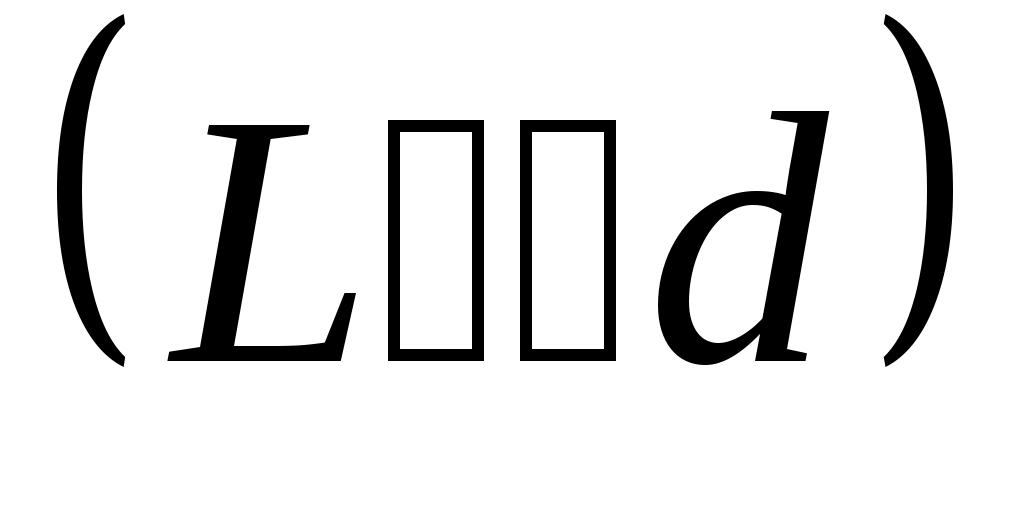 .
.
• Ширина интерференционной полосы
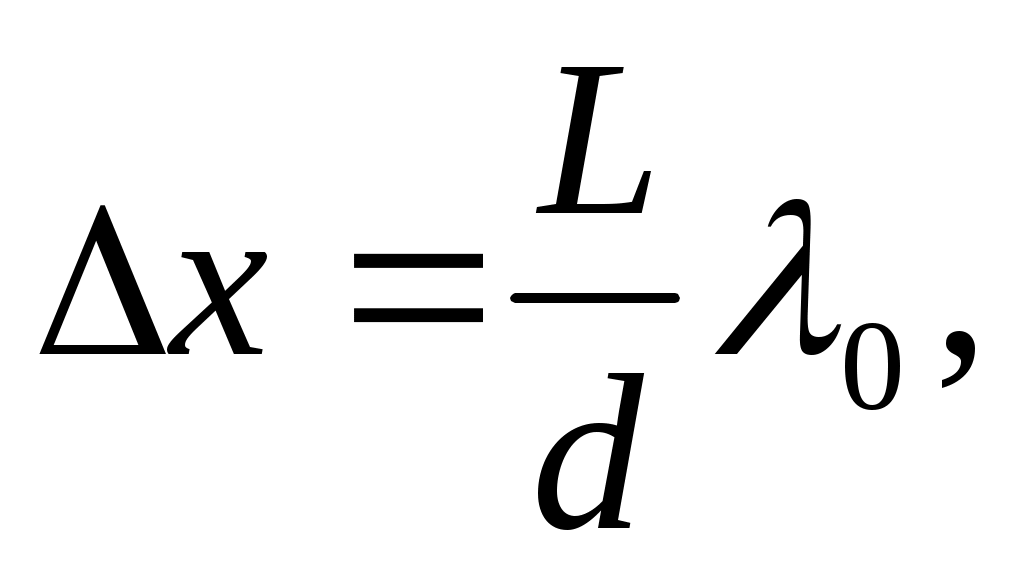
-
Оптическая разность хода при интерференции в тонких плёнках
в проходящем свете:
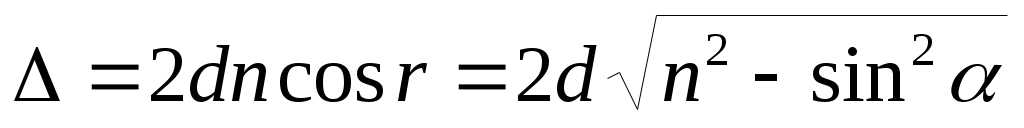 ,
,
в отражённом свете:
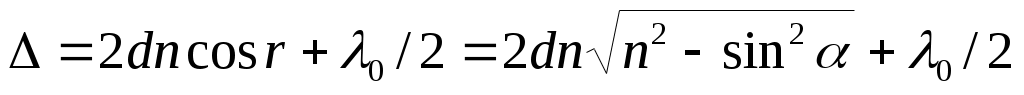
где d – толщина пленки; n – ее показательпреломления;– угол падения; r – угол преломления.
• Радиусы светлых колец Ньютона в отраженном свете (или темных в проходящем свете)
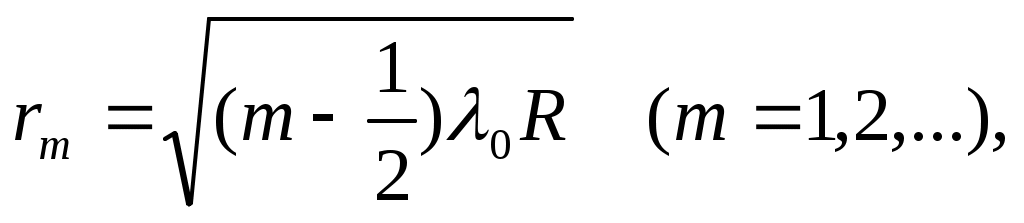

где m – номер кольца; R – радиус кривизны линзы.
• Радиусы темных колец Ньютона в отраженном свете (или светлых в проходящем свете)
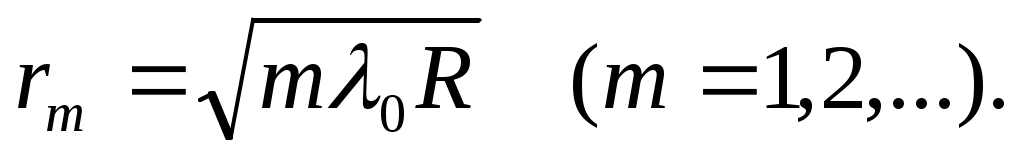
• В случае «просветления оптики» интерферирующие лучи в отраженном свете гасят друг друга при условии
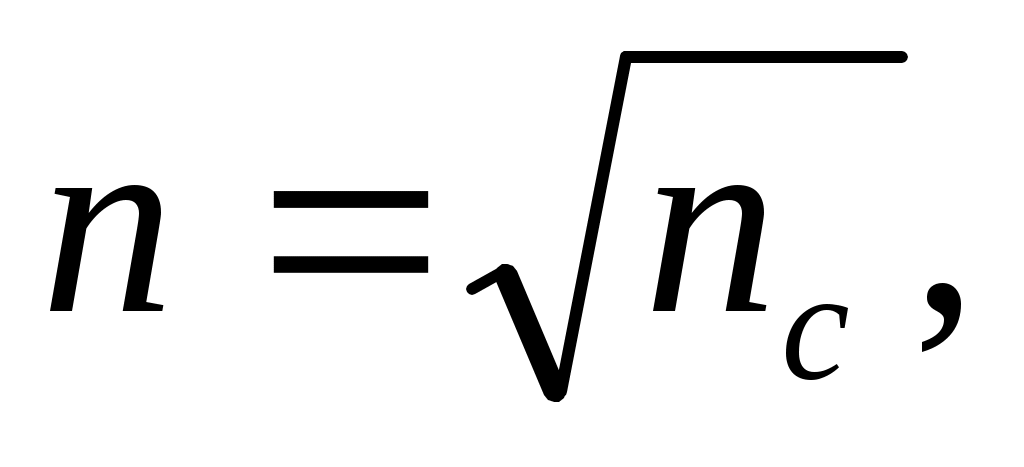
где nс – показатель преломления стекла; n – показатель преломления пленки.
Задания
1.1. Расстояние от щелей до экрана в опыте Юнга равно 1 м. Определить расстояние между щелями, если на отрезке длиной 1 см укладывается 10 темных интерференционных полос. Длина волны равна 0,7 мкм.
А.0,63 мм В.0,70 мм С.0,07 мм D.0,063 мм.
1.2. Две когерентные световые волны приходят в некоторую точку пространства с разностью хода 2,25 мкм. Каков результат интерференции в этой точке, если свет: а) красный (= 750 нм), б) зеленый (= 500 нм)?
А.а) усиление; б) ослабление В.а) усиление; б) усиление
С.а) ослабление; б) ослабление D.а) ослабление; б) усиление.
1.3. Разность хода двух интерферирующих лучей монохроматического света 0,3. Определить разность фаз колебаний.
А.108 В.18,84 рад С.1,08 D.3,14 рад.
1.4. Расстояние между двумя щелями в опыте Юнга равно 1 мм, расстояние от щелей до экрана 3 м, расстояние между максимумами яркости смежных интерференционных полос на экране 1,5 мм. Определить длину волны источника монохроматического света.
А.500 нм В.500 мкм С.0,5 нм D.0,05 мкм.
1.5. В опыте Юнга расстояние между щелями равно 1 мм, а расстояние от щелей до экрана равно 3 м. Определить: 1) положение первой светлой полосы; 2) положение третьей темной полосы, если щели освещать монохроматическим светом с длиной волны 0,5 мкм.
А.1) 1,5 мм; 2) 5,25 мм В.1) 5,25 мм; 2) 1,5 мм
С.1) 0,15 мм; 2) 0,525 мм D.1) 15 мм; 2) 5,25 мм.
1.6. Расстояние между двумя щелями в опыте Юнга равно 0,5 мм. Длина волны света равна 0,6 мкм. Определить расстояние от щелей до экрана, если ширина интерференционных полос равна 1,2 мм.
А.1 м В.0,1 м С.0,01м D.10 м.
1.7. Во сколько раз изменится ширина интерференционных полос на экране в опыте с зеркалами Френеля, если фиолетовый светофильтр (0,4 мкм) заменить красным (0,7 мкм).
А.1,75 В.17,5 С.0,175 D.0,0175.
1.8. Во сколько раз увеличится расстояние между соседними интерференционными полосами на экране в опыте Юнга, если зеленый светофильтр (=0,5 мкм) заменить красным (=0,65 мкм)?
А.В 1,3 раза В.В 13 раз С.В 0,13 раза D.В 130раз.
1.9. В опыте Юнга отверстия освещались монохроматическим светом длиной волны 600 нм, расстояние между отверстиями 1 мм и расстояние от отверстий до экрана 3 м. Найти положение трех первых полос.
А.1,8 мм; 3,6 мм; 5,4 мм В.18мм; 36 мм; 54 мм
С. 0,18 мм; 0,36 мм; 0,54 мм D.1,8 см; 3,6 см; 5,4 см.
1.10. В опыте с зеркалами Френеля расстояние между мнимыми изображениями источника света равно 0,5 мм, расстояние от них до экрана равно 5 м. В желтом свете ширина интерференционных полос равно 6 мм. Определить длину волны света.
А.0,6мкм В.0,6 мм С.60 мкм D.60 нм.
1.11*. Если в опыте Юнга на пути одного из интерферирующих лучей поместить перпендикулярно этому лучу тонкую стеклянную пластинку (n=1,5), то центральная светлая полоса смещается в положение, первоначально занимаемое пятой светлой полосой. Длина волны света равна 0,5 мкм. 5 мкм
1.12*. В опыте Юнга расстояние от щелей до экрана равно 3 м. Определить угловое расстояние между светлыми соседними полосами, если третья светлая полоса на экране отстоит от центра интерференционной картины на 4,5 мм. 5·10ˉ4 рад
1.13. На стеклянный клин (n=1,5) с малым углом нормально к его грани падает параллельный пучок лучей монохроматического света с длиной волны 0,698 мкм. Определить угол между поверхностями клина, если расстояние между двумя соседними интерференционными минимумами в отраженном свете равно 2 мм.
А. В.
В. С.
С. D.
D. .
.
1.14. На тонкий стеклянный клин (n=1,5) нормально падает монохроматический свет. Угол клина равен  . Определить длину световой волны, если расстояние между двумя соседними интерференционными максимумами в отраженном свете равно 0,2 мм.
. Определить длину световой волны, если расстояние между двумя соседними интерференционными максимумами в отраженном свете равно 0,2 мм.
А.698 нм В.1396 нм С.349 нм D.139,6 нм.
1.15. На стеклянный клин (n=1,5) падает нормально пучок света с длиной волны 0,582 мкм. Угол клина равен  . Какое число темных интерференционных полос приходится на единицу длины клина?
. Какое число темных интерференционных полос приходится на единицу длины клина?
А.5 полос на 1 см В.5 полос на 1 мм
С.4 полосы на 1 мм D.4 полосы на 1 см.
1.16*. Между двумя плоскопараллельными стеклянными пластинками (n=1,5) положили очень тонкую проволочку. Проволочка находится на расстоянии 75 мм от линии соприкосновения пластинок и ей параллельна. В отраженном свете с длиной волны 0,5 мкм на верхней пластинке видны интерференционные полосы. Определить толщину проволочки, если на протяжении 30 мм насчитывается 16 светлых полос. 10 мкм
1.17*. Между двумя плоскопараллельными стеклянными пластинками (n=1,5) на расстоянии 10 см от границы их соприкосновения находится проволока диаметром 0,01 мм, образуя воздушный клин. Пластины освещаются нормально падающим светом с длиной волны 0,6 мкм. Определить ширину интерференционных полос, наблюдаемых в отраженном свете. 3 мм
1.18*. Монохроматический свет падает нормально на поверхность воздушного клина, причем расстояние между интерференционными полосами равно 0,4 мм. Определите расстояние между интерференционными полосами, если пространство между пластинами, образующими клин, заполнить прозрачной жидкостью с показателем преломления n=1,33. 0,3 мм
1.19. Радиус второго темного кольца Ньютона в отраженном свете равен 0,4 мм. Определить радиус кривизны плосковыпуклой линзы, взятой для опыта, если она освещается светом с длиной волны 0,64 мкм.
А.125 мм В.1,25 мм С.12,5 мм D.125 см.
1.20. Между стеклянной пластинкой и лежащей на ней плосковыпуклой линзой находится жидкость. Найти показатель преломления жидкости, если радиус третьего темного кольца Ньютона при наблюдении в отраженном свете с длиной волны 0,6 мкм равен 0,82 мм. Радиус кривизны линзы равен 0,5 м.
А.1,34 В.8,92 С.0,134 D.0,892.
1.21. На стеклянную пластинку положена выпуклой стороной плосковыпуклая линза. Сверху линза освещена монохроматическим светом длиной волны 500 нм. Найти радиус кривизны линзы, если радиус четвертого темного кольца Ньютона в отраженном свете равен 2 мм.
А.2 м В.0,02 м С.0,2 м D.1 м.
1.22. Плосковыпуклая стеклянная линза (n=1,5) с фокусом 1 м лежит выпуклой стороной на стеклянной пластинке. Радиус пятого темного кольца Ньютона в отраженном свете равен 1,1 мм. Определить длину световой волны.
А.0,484 мкм В.0,242 мкм С.48,4 нм D.613 нм.
1.23. Установка для наблюдения колец Ньютона освещается нормально падающим монохроматическим светом с длиной волны 600 нм. Определить толщину воздушного промежутка в том месте, где в отраженном свете наблюдается первое светлое кольцо.
А.0,15 мкм В.0,15 мм С.1,5 мкм D.1,5 мм.
1.24. Расстояние между вторым и первым кольцами Ньютона в отраженном свете равно 1 мм. Определить расстояние между десятым и девятым.
А.0,39 мм В.0,039 мм С.0,78 мм D.0,078 мм.
1.25. Диаметр второго светлого кольца Ньютона при наблюдении в отраженном свете с длиной волны 0,6мкм равен 1,2 мм. Определить оптическую силу плосковыпуклой линзы, взятой для опыта.
А.1,25 дптр В.0,125 дптр С.12,5 дптр D.0,0125 дптр.
1.26. Плосковыпуклая линза с оптической силой 2 дптр выпуклой стороной лежит на стеклянной пластинке. Радиус четвертого темного кольца Ньютона в отраженном свете равен 0,7 мм. Определить длину световой волны.
А.0,49 мкм В.4,9 мкм С.49 нм D.049 нм.
1.27. Плосковыпуклая линза радиусом кривизны 4 м выпуклой стороной лежит на стеклянной пластинке. Определить длину волны падающего монохроматического света, если радиус пятого светлого кольца в отраженном свете равен 3 мм.
А.0,5 мкм В.5,0 мкм С.50 нм D.0,5 нм.
1.28. Установка для наблюдения колец Ньютона освещается нормально падающим монохроматическим светом с длиной волны 550 нм. Определить толщину воздушного промежутка в том месте, где в отраженном свете наблюдается четвертое темное кольцо.
А.1,1 мкм В.1,1 нм С.11 мкм D.11 нм.
1.29. Установка для наблюдения колец Ньютона освещается нормально падающим монохроматическим светом с длиной волны 600 нм. Пространство между линзой и стеклянной пластинкой заполнено жидкостью, и наблюдение ведется в проходящем свете. Радиус кривизны линзы равен 4 м. Определить показатель преломления жидкости, если радиус второго светлого кольца равен 1,8 мм.
А.1,48 В.1,11 С.1,21 D.1,31.
1.30. Плосковыпуклая линза с показателем преломления n=1,6 выпуклой стороной лежит на стеклянной пластинке. Радиус третьего светлого кольца в отраженном свете с длиной волны 0,6 мкм равен 0,9 мм. Определить фокусное расстояние линзы.
А.0,9 м В.9 м С.0,09 м D.9 мм.
1.31. Плосковыпуклая линза с радиусом сферической поверхности 12,5 см прижата к стеклянной пластинке. Диаметр десятого темного кольца Ньютона в отраженном свете равен 1 мм. Определите длину волны света.
А.0,2 мкм В.0,2 нм С.2 нм D.20 мкм.
1.32. Установка для наблюдения колец Ньютона освещается монохроматическим светом, падающим нормально. При заполнении пространства между линзой и стеклянной пластинкой прозрачной жидкостью радиусы темных колец в отраженном свете уменьшились в 1,21 раза. Определить показатель преломления жидкости.
А.1,46 В.1,26 С.1,36 D.1,56.
1.33*. Найти радиус центрального темного пятна колец Ньютона, если между линзой и пластинкой налит бензол (n=1,5). Радиус кривизны линзы равен 1 м. Показатели преломления линзы и пластинки одинаковы. Наблюдение ведется в отраженном свете с длиной волны 589 нм. 0,63 мм
1.34. На мыльную пленку с показателем преломления n=1,33 падает по нормали монохроматический свет с длиной волны 0,6 мкм. Отраженный свет в результате интерференции имеет наибольшую яркость. Какова возможная наименьшая толщина пленки?
А.0,113 мкм В.0,113 нм С.1,13 мкм D.1,13 нм.
1.35. На тонкую пленку в направлении нормали к ее поверхности падает монохроматический свет с длиной волны 500 нм. Отраженный от нее свет максимально усилен вследствие интерференции. Определить минимальную толщину пленки, если показатель преломления материала пленки равен 1,4.
А.89 нм В.8,9 нм С.0,89 мкм D.89 мкм.
1.36. На тонкую глицериновую пленку толщиной 1,5 мкм нормально к ее поверхности падает белый свет. Определить число длин волн лучей видимого участка спектра (0,4 ≤ λ ≤ 0,8 мкм), которые будут ослаблены в результате интерференции в проходящем свете. Показатель преломления глицерина равен 1,47.
А.5 В.6 С.7 D.4.
1.37. На стеклянную пластинку нанесен тонкий слой прозрачного вещества с показателем преломления n=1,3. Пластинка освещена параллельным пучком монохроматического света с длиной волны 640 нм, падающим на пластинку нормально. Какую минимальную толщину должен иметь слой, чтобы отраженный пучок имел наименьшую яркость?
А.0,123 мкм В.1,23 мкм С.12,3 мкм D.123 мкм.
1.38. Пучок параллельных лучей с длиной волны 0,6 мкм падает под углом 30˚ на мыльную пленку с показателем преломления n=1,33. При какой возможной наименьшей толщине пленки отраженные лучи будут максимально ослаблены интерференцией? Максимально усилены?
А.0,243 мкм; 0,122 мкм В.0,122 мкм; 0,243 мкм
С.2,43 мкм; 1,22 мкм D.1,22 мкм; 2,43 мкм.
1.39. Пучок белого света падает нормально на стеклянную пластинку, толщина которой равна 0,4 мкм. Показатель преломления стекла равен 1,5. Какие длины волн, лежащие в пределах видимого спектра (0,4 ≤ λ ≤ 0,7 мкм), усиливаются в отраженном пучке?
А.0,48 мкм В.4,8 мкм С.48 мкм D.480 мкм.
1.40. На мыльную пленку с показателем преломления n=1,33 падает белый свет под углом 45˚. При какой наименьшей толщине пленки отраженные лучи будут окрашены в желтый цвет?
А.0,13 мкм В.1,3 мкм С.13 мкм D.13 нм.
1.41*. Темной или светлой будет в отраженном свете мыльная пленка толщиной d = 0,1λ? Пленка находится в воздухе, показатель преломления пленки равен 1,3. Считать, что пучок света падает на пленку нормально. темной
1.42*. Зимой на стеклах трамваев и автобусов образуются тонкие пленки наледи, окрашивающие все видимое сквозь них в зеленоватый цвет. Оценить, какова наименьшая толщина этих пленок (показатель преломления наледи принять равным 1,33).
0,5 мкм
Координаты максимумов и минимумов интенсивности в опыте Юнга
Оптическая разность хода при интерференции в тонких плёнках
1.43*. На поверхность стеклянного объектива (n1=1,5) нанесена тонкая пленка, показатель преломления которой n2=1,2 («просветляющая» пленка). При какой наименьшей толщине этой пленки произойдет максимальное ослабление отраженного света в средней части видимого спектра? 0,115 мкм
1.44*. На линзу с показателем преломления n = 1,58 нормально падает монохроматический свет с длиной волны 0,55мкм. Для устранения потерь света в результате отражения на линзу наносится тонкая пленка. Определить: 1) оптимальный показатель преломления для пленки;
2) толщину пленки. 1) 1,26; 2) 109 нм
1.45*. Тонкая пленка с показателем преломления n=1,5 освещается светом с длиной волны 600 нм. При какой минимальной толщине пленки исчезнут интерференционные полосы? 100 нм
2. ДИФРАКЦИЯ И ПОЛЯРИЗАЦИЯ СВЕТА
Основные формулы и законы
-
Радиус внешней границы m-йзоны Френеля для сферической волны
где m— номер зоны Френеля; — длина волны;
-
Условия дифракционных максимумов и минимумов от одной щели, на которую свет падает нормально:
-
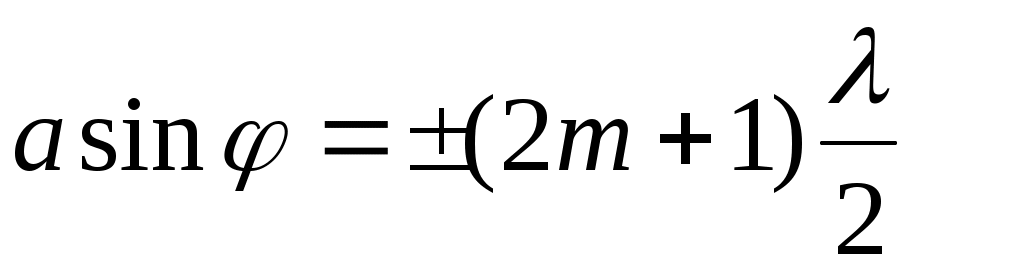
условие максимума
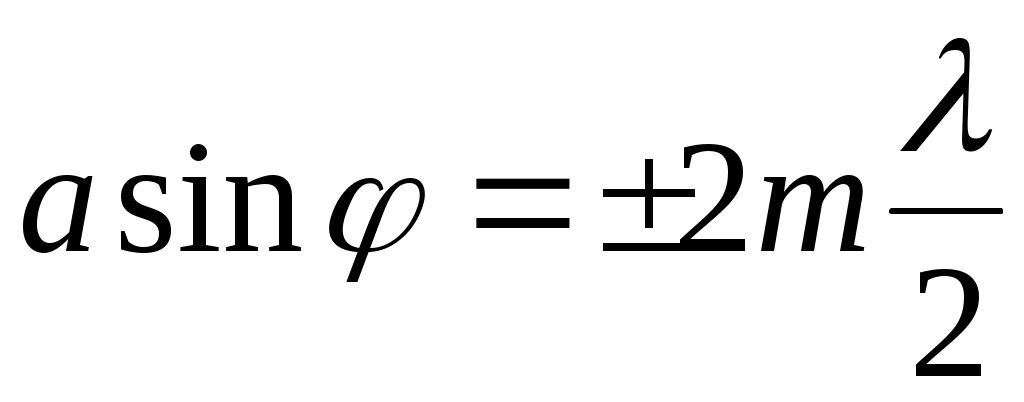
условие минимума
(m = 1, 2, 3, ...),
где
— длина волны.
-
Условия главных максимумов и дополнительных минимумов дифракционной решетки, на которую свет падает нормально:
- (k= 1, 2, 3...) – условие минимума
где d— период (постоянная) дифракционной решетки; N — число штрихов решетки.
-
Период дифракционной решетки
где No— число щелей, приходящихся на единицу длины решетки.
-
Условие дифракционных максимумов от пространственной решетки (формула Вульфа — Брэггов)
где d— расстояние между атомными плоскостями кристалла; — угол скольжения.
-
Угловая дисперсия дифракционной решетки
-
Разрешающая способность дифракционной решетки
где , ( + ) — длины волн двух соседних спектральных линий, разрешаемых решеткой; m— порядок спектра; N — общее число штрихов решетки.
-
Закон Малюса
где I – интенсивность плоскополяризованного света, прошедшего через анализатор; I0 – интенсивность плоскополяризованного света, падающего на анализатор; - угол между главными плоскостями поляризатора и анализатора.
-
Закон Брюстера
где
-
Угол поворота плоскости поляризации:
для оптически активных кристаллов и чистых жидкостей
для оптически активных растворов
,
где d – длина пути, пройденного светом в оптически активном веществе; ([]) – удельное вращение; С – массовая концентрация оптически активного вещества в растворе.
ЗАДАНИЯ
2.1. Посередине между точечным источником монохроматического света ( = 550 нм) и экраном находится диафрагма с круглым отверстием. Дифракционная картина наблюдается на экране, расположенном на расстоянии 5 м от источника. Определите радиус отверстия, при котором центр дифракционных колец, наблюдаемых на экране, будет наиболее темным.
А. [1,17 мм] В. [1,17 м] С. [11,7 мм] D. [0,117 мм]
2.2 На мыльную пленку с показателем преломления n=1,33 падает белый свет под углом 45˚. При какой наименьшей толщине пленки отраженные лучи будут окрашены в желтый цвет?
А. [2 м] В.[ 0,2 м] С. [0,5 м] D. [20 м]
2.3. Определите радиус третьей зоны Френеля, если расстояния от точечного источника света (= 0,6 мкм) до волновой поверхности и от волновой поверхности до точки наблюдения равны 1,5 м.
А. [1,16 мм] В. [1,5 мм] С. [11,6 мм] D. [0,6 мм]
2.4. На диафрагму с круглым отверстием диаметром 5 мм падает нормально параллельный пучок света с длиной волны 0,6 мкм. Определите расстояние от точки наблюдения до отверстия, если отверстие открывает: 1) две зоны Френеля; 2) три зоны Френеля.
А. [1) 5,21 м; 2) 3,47 м] В. [1) 5,21 мм; 2) 3,47 м]
С. [1) 52,1 м; 2) 34,7 м] D. [1) 5,21 м; 2) 3,47 мм]
2.5. Определите радиус третьей зоны Френеля для случая плоской волны. Расстояние от волновой поверхности до точки наблюдения равно 1,5 м. Длина волны 0,6 мкм.
А. [1,64 мм] В. [1,5 м] С. [16,4 мм] D. [0,6 мм]
2.6. Определите радиус четвертой зоны Френеля, если радиус второй зоны Френеля для плоского волнового фронта равен 2 мм.
А. [2,83 мм] В. [2,0 мм] С. [28,3 мм] D. [2,5 мм]
2.7. Определите радиус первой зоны Френеля, если расстояния от точечного источника света ( = 0,5 мкм) до зонной пластинки и от пластинки до места наблюдения 1 м.
А. [0,5 мм] В. [0,5 м] С. [2,5 мм] D. [1,0 мм]
2.8. На зонную пластинку падает плоская монохроматическая волна ( = 0,5 мкм). Определите радиус первой зоны Френеля, если расстояние от зонной пластинки до места наблюдения 1 м.
А. [707 мкм] В. [7,07 мкм] С. [707 мм] D. [70,7 мкм]
2.9. Дифракция наблюдается на расстоянии
А. [50 м] В. [0,5 м] С. [5,0 м] D. [50 мм]
2.10. Какой должна быть ширина щели, чтобы первый дифракционный минимум наблюдался под углом 90° при освещении: 1) красным светом (1 =760 нм)? 2) синим светом (2 = 440 нм)?
А. [1) 7,610-5 см; 2) 4,410-5 см] В. [1) 7,610-8 см; 2) 4,410-8 см]
С. [1) 7,610-3 см; 2) 4,410-3 см] D. [1) 7,610-7 см; 2) 4,410-7 см]
2.11. На щель падает нормально монохроматический свет. Угол отклонения лучей, соответствующих второму минимуму, равен 2°18'. Скольким длинам волн падающего света равна ширина щели?
А. [50] В. [20] С. [70] D. [10]
2.12. Длина волны падающего на щель нормально монохроматического света укладывается в ширине щели 6 раз. Под каким углом будет наблюдаться третий дифракционный минимум света?
А. [30°] В. [90°] С. [60°] D. [45°]
2.13. На щель шириной 0,1мм падает нормально монохроматический свет ( = 0,6 мкм). Экран, на котором наблюдается дифракционная картина, расположен параллельно щели на расстоянии 1 м. Определите расстояние между первыми дифракционными минимумами, расположенными по обе стороны центрального максимума.
А. [1,2 см] В. [0,12 см] С. [12 см] D. [1,8 см]
2.14. На дифракционную решетку нормально падает монохроматический свет с длиной волны 600 нм. Определите наибольший порядок спектра, полученный с помощью этой решетки, если ее постоянная равна 2 мкм.
А. [3] В. [7] С. [5] D. [9]
2.15. На дифракционную решетку длиной 1,5 мм, содержащую 3000 штрихов, падает нормально монохроматический свет с длиной волны 550 нм. Определите: 1) число максимумов, наблюдаемых в спектре дифракционной решетки; 2) угол, соответствующий последнему максимуму.
А. [1) 18; 2) 81°54'] В. [1) 25; 2) 60°54']
С. [1) 20; 2) 45°54'] D. [1) 10; 2) 30°54']
2.16. Определите число штрихов на 1 мм дифракционной решетки, если углу = 30° соответствует максимум четвертого порядка для монохроматического света с длиной волны 0,5 мкм.
А. [250 мм-1] В. [25 мм-1] С. [350 мм-1] D. [250 м-1]
2.17. Период дифракционной решетки 0,005 мм. Определить число наблюдаемых главных максимумов в спектре дифракционной решетки для: 1) = 760 нм; 2) = 440 нм.
А. [1) 13; 2) 23] В. [1) 10; 2) 20] С. [1) 18; 2) 28] D. [1) 5; 2) 10]
2.18. Сколько штрихов на 1 мм должна иметь дифракционная решетка, чтобы углу = 90° соответствовал максимум 5-го порядка для света с длиной волны = 500 нм?