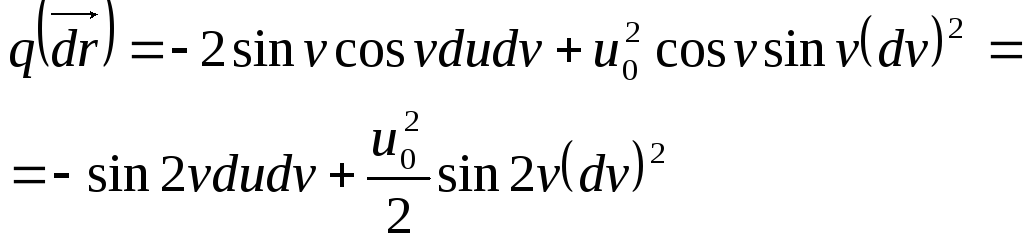ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 18.04.2024
Просмотров: 153
Скачиваний: 0
СОДЕРЖАНИЕ
Б.1в1 Различные способы задания прямой.
Взаимное расположение прямой и плоскости
В.2 Линии и поверхности 2-ого порядка в аффинных и евклидовых пространствах, канонические уравнения.
Б1.В3Топологич пр-ва.Гомеоморф.Примеры
Первая квадратичная форма поверхности.
9.Найти эйлерову характеристику сферы .
Решение. Сфера в 3-мерном пространстве – это 2-мерное компактное связное отделимое многообразие без края.
Впишем в сферу
![]() тетраэдр -
тетраэдр -
![]() треугольная пирамида симплекс-3-мерном
пр-ве
треугольная пирамида симплекс-3-мерном
пр-ве
Тетраэдр
![]() - двумерное компактное связное отделимое
многообразие без края.
- двумерное компактное связное отделимое
многообразие без края.
Рассмотрим
ортогональное проектирование
![]() из центра
из центра
![]() такое, что для
такое, что для
![]() ставим в соответствие
ставим в соответствие
![]() .
Ортогональное проектирование
.
Ортогональное проектирование
![]() -это
гомеоморфизм, т.е.оно взаимно однозначно
и взаимно непрерывно.
-это
гомеоморфизм, т.е.оно взаимно однозначно
и взаимно непрерывно.
![]()
![]() и
и
![]() гомеоморфны.
гомеоморфны.
Эйлерова характеристика
![]() ,
где
,
где
![]() -
вершины,
-
вершины,
![]() -
ребра,
-
ребра,
![]() -грани.
-грани.
![]() .
.
Но эйлерова
характеристика – это топологический
инвариант, т.е.она сохраняется при
![]() гомеоморфизмах..
гомеоморфизмах..
![]() эйлерова
характеристика сферы
эйлерова
характеристика сферы
![]()
![]() .
.
Замечание. Эйлерова характеристика применима только к компактным многообразиям.
----------------------------------------------------------------------------------------------
10.найти
точку пересечения касательной к линии
![]() ,
,
![]() ,
,
![]() в точке касания
в точке касания
![]() с плоскостью
с плоскостью
![]() .
.
Решение.
![]()
![]()
![]()
![]() ,
,
![]()
Теорема. В каждой
точке
![]() гладкой линии
гладкой линии
![]() ,
заданной ур-ем
,
заданной ур-ем
![]() ,
сущ-т касательная прямая, которая
опред-ся точкой
,
сущ-т касательная прямая, которая
опред-ся точкой
![]() и направляющим вектором
и направляющим вектором
![]() .
.
![]() .
.
Т.к.рассматр.пересечение
с
![]() ,
то координата по
,
то координата по
![]() .
.
При
![]() имеем точку
имеем точку
![]() .
.
11. написать
уравнение касательной плоскости и
рнормали к геликоиду, заданному
уравнениями
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
в точке
,
в точке
![]() .
.
Решение.
Уравнение касательной плоскости
![]()
Уравнение нормали:
![]()
В точке
![]() :
:
![]()
![]()
Найдем
![]() :
:

![]() .
.
Уравнение касательной
плоскости:
![]() .
.
Но
![]() ,
,
![]() ,
,
![]() .
Поэтому
.
Поэтому
![]()
Уравнение нормали
![]()
12.найти первую квадратичную форму геликоида
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Решение:
Квадр форма
![]() назыв первой квадратич формой поверхности
назыв первой квадратич формой поверхности
![]() .
.
![]()
![]()
![]() ,
,
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()