ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 18.04.2024
Просмотров: 147
Скачиваний: 0
СОДЕРЖАНИЕ
Б.1в1 Различные способы задания прямой.
Взаимное расположение прямой и плоскости
В.2 Линии и поверхности 2-ого порядка в аффинных и евклидовых пространствах, канонические уравнения.
Б1.В3Топологич пр-ва.Гомеоморф.Примеры
Первая квадратичная форма поверхности.
![]() :
:![]()
![]() .
.
Составим определитель
вида
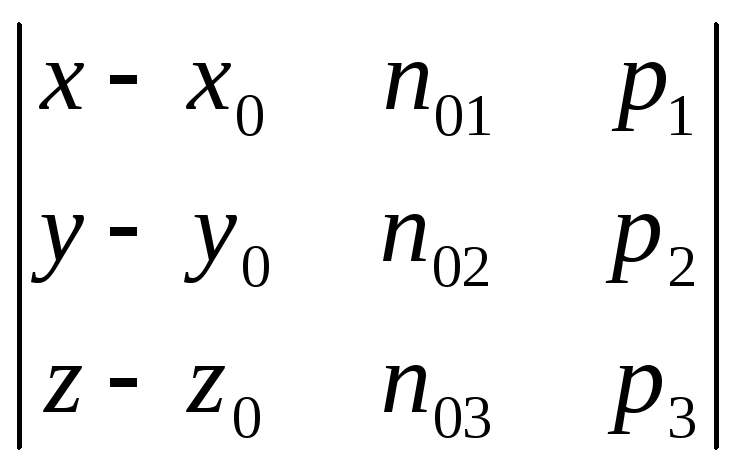 , где
, где
![]() ,
,
![]()
![]() ,
,
![]()
![]()
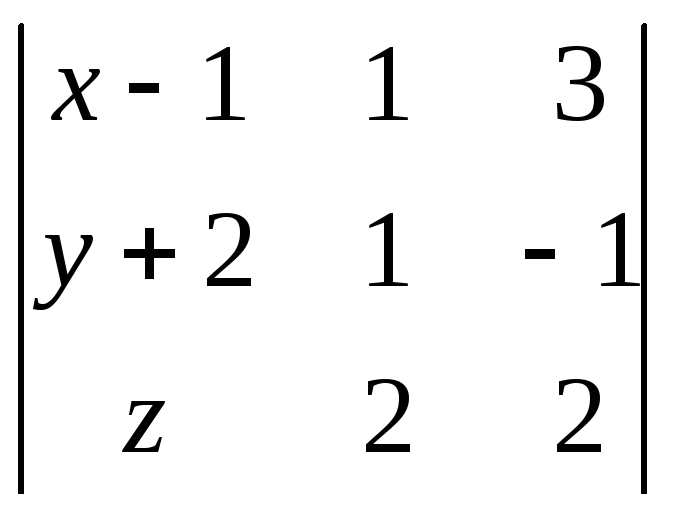
![]()
![]()
![]() .-
ур-ие искомой пл-ти.
.-
ур-ие искомой пл-ти.
Задача 4 определить тип поверхности
Решение:
Сгруппируем
![]()
Упростим и получим выражение вида
![]()
Рассмотрим общий вид уравнения эллипсоида
![]()
Где a,b,c- полуоси,(0,0,0)- центр.
Следовательно
уравнение
![]() это уравнения эллипсоида со смещенным
центром (2,-1,2)и полуосями
это уравнения эллипсоида со смещенным
центром (2,-1,2)и полуосями
![]() .
.
---------------------------------------------------------------
5.парабола
с параметром
![]() расположена на плоскости
расположена на плоскости
![]() так, что директриса совпадает с осью
так, что директриса совпадает с осью
![]() .
написать ур-ие поверхности, образованной
вращением параболы вокруг оси
.
написать ур-ие поверхности, образованной
вращением параболы вокруг оси
![]()
Решение:
Найдем ур-ие пов-ти вращения. В общем виде:
![]() .
.
![]() найдем из ур-ия
линии
найдем из ур-ия
линии
![]() ,
,
![]() ,
,
![]()
Подставим в общее ур-ие
![]()
![]()
![]()
![]() - искомое ур-ие
пов-ти в общем виде.
- искомое ур-ие
пов-ти в общем виде.
Для
![]() :
:
![]()
Ответ:
![]() .
.
6.привести
к каноническому виду ур-ие пов-ти
![]() .
.
Решение.
![]()
![]()
![]()
Сделаем замену:
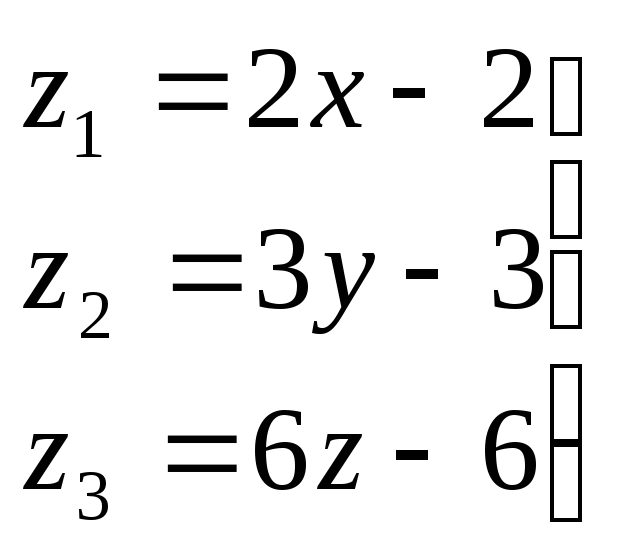
![]()
![]() .
.
------------------------------------------------------------------------------------------------
7.являются ли непрерывными и гомеоморфными отображения:
А)![]() ,
где
,
где
![]() - единичная окружность, заданная по
правилу :
- единичная окружность, заданная по
правилу :
![]()
![]()
Решение:
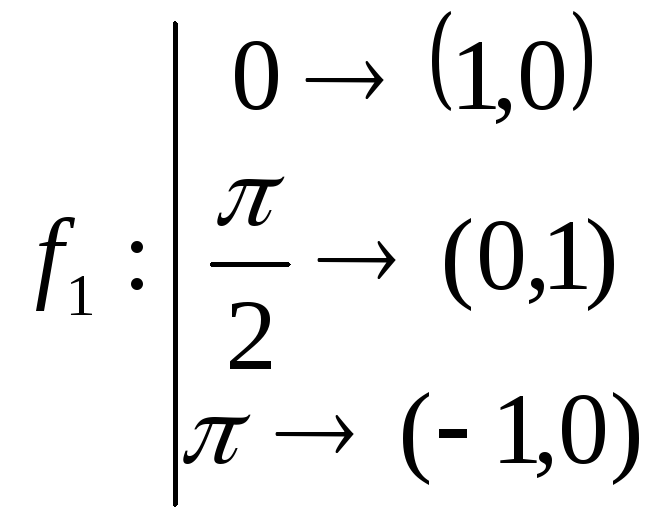
![]() ,
,
![]() ,
,
![]()
![]() существует
существует
![]()
![]()
Опред. Отображение
![]() наз непрер в
наз непрер в
![]() ,
если для
,
если для
![]() окрестности
окрестности
![]() точки
точки
![]() найдется окрестность
найдется окрестность
![]() :
:
![]()
По определ имеем
![]() ,
,![]() .
.
Определение
выполняется для
![]() точки
точки
![]() отображение
непрерывно.
отображение
непрерывно.
Опред. Отображение
![]() наз гомеоморфным, если оно взаимно
однозначно и взаимно непрерывно
наз гомеоморфным, если оно взаимно
однозначно и взаимно непрерывно
Очевидно, что
![]() - непрерыв.отображ, но и обратное отобр.
- непрерыв.отображ, но и обратное отобр.
![]() нет явл непрерыв,
т.к.происходит разрыв в т окружности
нет явл непрерыв,
т.к.происходит разрыв в т окружности
![]() .
.
![]()
![]()
![]() обратное
отображение не явл непрерывным
обратное
отображение не явл непрерывным
![]()
![]() не явл гомеоморфизмом.
не явл гомеоморфизмом.
Б)![]() ,
где
,
где
![]() -
полуокружность единичной окружности
-
полуокружность единичной окружности
![]() ,
расположенная в полуплоскости
,
расположенная в полуплоскости
![]() ,
заданная по правилу:
,
заданная по правилу:
![]()
![]()
Решение
![]()
![]() :
:
![]()
![]() отображ
непрер. Аналогично обратное отображение
отображ
непрер. Аналогично обратное отображение
![]() также непрерывно
также непрерывно
Ответ : это гомеоморфизм по определению.
8.Показать что интервал гомеоморферфен числовой прямой, полуинтервал гомеоморфен лучу, а интервал - открытому лучу.
Решение.
Рассмотрим функциюс![]() ,
,
![]() ,
,
![]() .
.
График функции
задает отображение
![]() ,
где
,
где
![]() -ось
-ось
![]() .
.
![]() отображение
явл биективным (взаимно однозначным).
отображение
явл биективным (взаимно однозначным).
Докажем это.
Действит-но, каждая т на оси
![]() соответствует 1 и только одной точке
интервала.
соответствует 1 и только одной точке
интервала.
Непрерывность
очевидна из графика. По определению для
![]() окрестности
окрестности
![]() для
для
![]()
![]() окрестность
окрестность
![]() точки
точки
![]() ,
такая , что
,
такая , что
![]() .
.
![]() отображение
непрер для
отображение
непрер для
![]() точки
точки
![]() отображение непрер. Ч.т.д.
отображение непрер. Ч.т.д.
Аналогично обратное
отображение
![]() также непрерывно.
также непрерывно.
![]()
![]() -гомеоморфизм
-гомеоморфизм
![]()
![]() (
(![]() - гомеоморфен). Сужение этого отображения
на
- гомеоморфен). Сужение этого отображения
на
![]() дает гомеоморфизм.
дает гомеоморфизм.
![]() - замкнутый луч (мн-во всех неотриц
чисел). Сужение
- замкнутый луч (мн-во всех неотриц
чисел). Сужение
![]() дает гомеоморфизм
дает гомеоморфизм
![]() - открытый луч.
- открытый луч.