Файл: Геометрия.doc

Контрпримеры: не являются элементарными следующие поверхности: сфера (её можно покрыть двумя полусферами); эллипсоид (он гомеоморфен сфере), эллиптический цилиндр (его можно покрыть конечным числом цилиндрических полос, гомеоморфных плоскости); однополостный гиперболоид (гомеоморфен эллиптическому цилиндру)

двуполостный гиперболоид (покрывается двумя своими полостями, каждая из которых гомеоморфна плоскости); гиперболический цилиндр и т.д

О пр 4: Точка M поверхности F называется обыкновенной, если у этой точки как точки пространства существует - окрестность B(M, ), такая, что F∩ B(M, )является элементарной поверхностью. Если пересечение гомеоморфно плоскости, то точка называется внутренней, если замкнутой полуплоскости – граничной. Опр 5: Точка M F называется особой, если она не является обыкновенной. Пр: Рассмотрим цилиндрическую поверхность, которая сама себя пересекает по прямой MN. Каждая точка этой прямой является особой

М

N

Опр 6: Поверхность, все точки котобыкновенные, наз простой.

---

Опр7: Множество всех граничных точек простой поверхности называется её краем (границей). Примеры: 1) Всякая элементарная поверхность является простой. 2) Сфера, эллипсоид, эллиптический цилиндр, гиперболоиды – простые поверхности.3) Коническая поверхность не является простой, т.к. её вершина – особая точка. Замечания: 1) Любая поверхность, гомеоморфная квадрату, является поверхностью с краем, причем край гомеоморфен окружности. 2) Всякая поверхность, гомеоморфная замкнутой полуплоскости () также является поверхностью с краем, но край гомеоморфен прямой. 3) Всякая простая поверхность является двумерным многообразием (или двумерным многообразием с краем). В дальнейшем будем изучать простую поверхность F в некоторой -окрестности B(M, ), её внутренней точки M. Очевидно, что всегда можно выбрать настолько малым, что пересечение) F∩ B(M, ) будет гомеоморфно плоскости. Будем обозначать через G плоскую область, гомеоморфную плоскости (или R²), а через F₀ = F∩ B(M, ) - элементарную поверхность, гомеоморфную G. Зададим в пространстве E₃ п.с.к. и рассмотрим гомеоморфизм f: G→F₀ (см приложение 1)

Если точка (u,v) переходит в точку M(x,y,z)F₀, то ясно, что x,y,z являются функциями (непрерывными) от переменных u и v:

x=x(u,v); y=y(u,v); z=z(u,v), (1) определёнными в области G.(1)– параметрические уравнения поверхности F₀. Уравнения (1) эквивалентны векторному уравнению:

, (2) _где - радиус-вектор точки M. Уравнение (2) коротко можно записать в виде: . (3) – векторная функция двух скалярных аргументов u,v, определенная в G(области G)(см приложение 2). G – открытая область в плоскости Oxy; z=f(x,y) – явное ур-ие поверхности F₀. Гладкие поверхности. Пусть F₀ – элементарная поверхность, заданная параметрическими уравнениями: x=x(u,v); y=y(u,v); z=z(u,v), (1) где функции в правых частях определены в плоской области G. Опр 1: Элементарная поверхность называется гладкой класса C^k (kN), если правые части уравнений (1) являются функциями, имеющими в области G непрерывные частные производные до порядка k включительно, причем в точке (u,v) ранг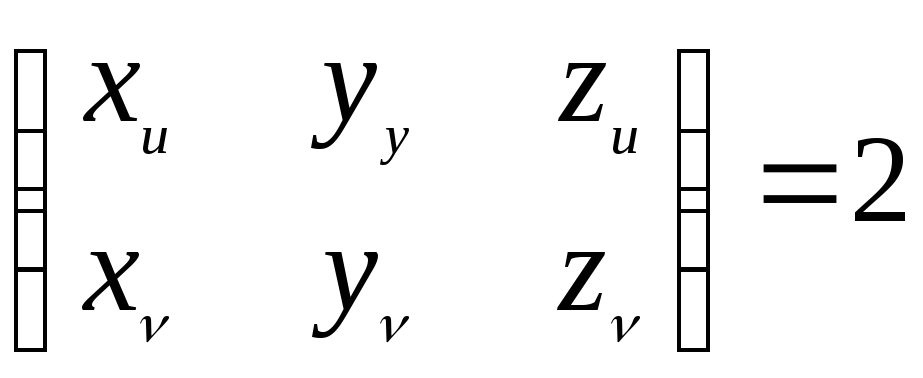 (2) Опр 2: Простая поверхность F называется гладкой класса C^k, если у каждой её внутренней точки M существует ε-окрестность B(M, ε), такая, что F∩ B(M, ε) - гладкая элементарная поверхность класса C^k.

---

Первая квадратичная форма поверхности.

Опр1: Квадратичная форма = наз первой квадратичной формой поверхности F₀ (или её линейным элементом). Таким образом, первая квадратичная форма поверхности имеет значение квадрата линейного элемента ds (дифференциала длины дуги s гладкой линии на этой поверхности при бесконечно малом смещении точки вдоль этой линии).Формула для вычисления длины дуги линии с концами M₁(t₁); M₂(t₂):

s=

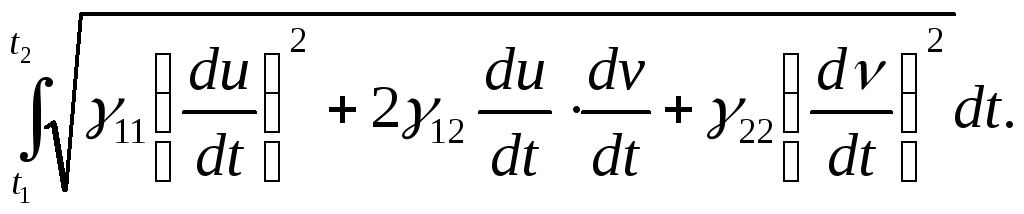
1. написать ур-е плоскости, проходящей через т и перпендикулярной к прямой . Написать ур-ие пл-ти, содержащей т и прямую .

Решение.

, .

,

Построим плоскость , содержащую и т .

,

---

: .

Теперь построим плоскость, пох-ую ч-з и : плоскости = прямой

-уравнение искомой плоскости.

---------------------------------------------------------------

2.составить ур-ие пл-ти, касательной к сфере . В точке

Решение:

Подставим координаты т в ур-ие сферы:

сфере

:

3.

Найти ур-ие плоскости, проходящей ч-з прямую перпендикулярно к плоскости

Решение:

По уравнению прямой видно, что искомой плоскости

---