Файл: Г.М. Гринфельд лекции по курсу дискретные системы автоматического управления.doc

(22)

(23)

где - дискретные передаточные функции прямого канала и разомкнутой системы, соответственно.

Для системы, рассматриваемой в данном примере:

,

Следовательно,

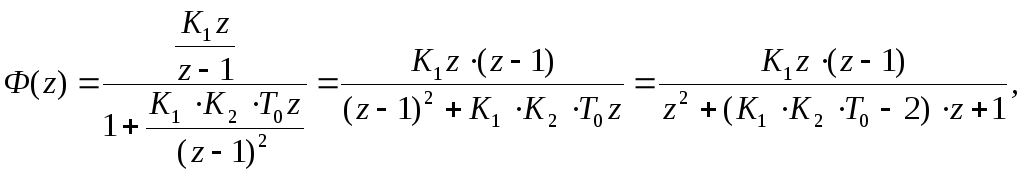
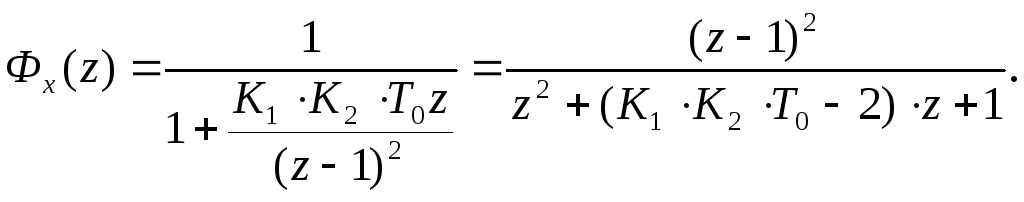
2.6. Обратное z-преобразование.

Определив дискретные передаточные функции ии, знаяZ-изображение входного сигнала, можно вычислитьZ-изображение выходного сигнала или сигнала ошибки:

.

По Z-изображениям сигналов системы могут быть найдены соответствующие решетчатые функции. Такая операция представляет собой обратноеZ-преобразование, символическое обозначение которой -.

Не следует забывать, что получаемая в результате обратного Z-преобразования решетчатая функцияопределяет значения непрерывного сигналатолько в дискретные моменты времени. Поэтому для полного описания функциинеобходимо использовать дополнительную информацию о поведении системы, либо применять методы, позволяющие вычислить величинувнутри интервалов квантования. К числу таких методов относятся рассматриваемые в последующих разделах данного курса методы дробного квантования и модифицированногоZ-преобразования.

По изображению произвольного вида значениямогут быть вычислены путем разложенияв ряд Лорана (в ряд по убывающим степеням (z)):

(24)

Сравнивая приведенный ряд с (12), получим:

Поскольку для каждого изображения в ряд (24) является единственным, оно может быть осуществлено любым способом, например по формулам:

Наиболее простым приемом нахождения коэффициентов ряда (24) в случае, когда представлено в виде дробно-рациональной функции

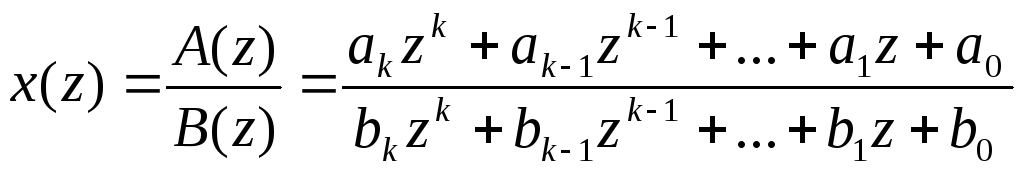(25)

является деление числителя на знаменатель.

Пример 14. Необходимо определить решетчатую переходную функцию системы с передаточной функцией:

Z-изображение решетчатой переходной функции:

В результате деления полинома, стоящего в числителе , на полином в знаменателе, получим:

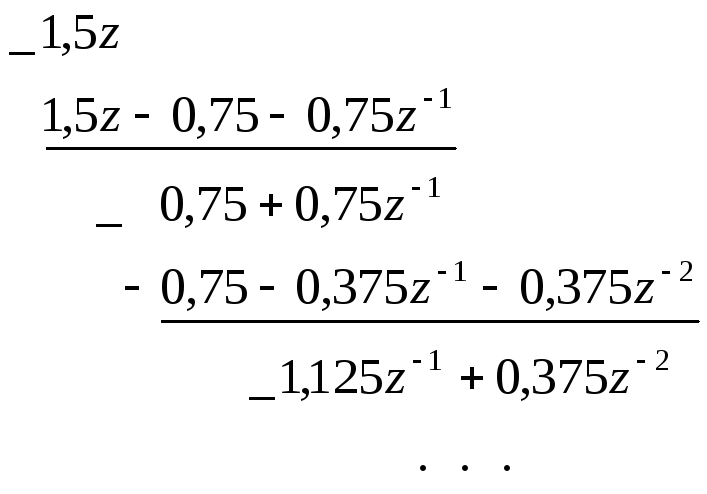
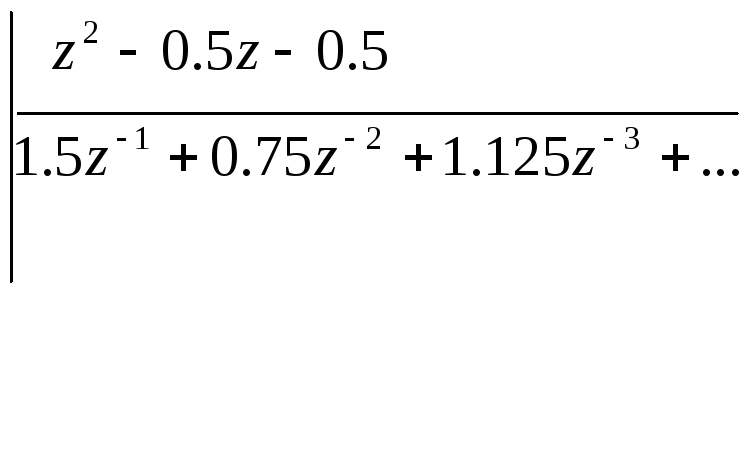
Коэффициенты полученного степенного ряда определяют следующие дискреты (рис. 21):

;;и т.д.

Использование любого из предложенных методов расчета дискрет решетчатой функции не ограничено какими-либо условиями к виду , но не дает возможности записать выражение дляв виде компактной функции натурального аргумента.

Такая функция может быть получена на основании формулы обратного Z-преобразования (формулы обращения):

.

(26)

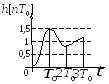
Рис.21. Решетчатая переходная функция

(пример 14)

где замкнутый контур интегрирования Г на плоскостиZохватывает особые точки.

Вычисление интеграла (26) может быть осуществлено с использованием формулы Коши в полюсах :

. (27)

Вычет в простом полюсе находится по формуле:

, (28)

а вычет в полюсе кратности S:

. (29)

Если полюса изображения (25) простые, , а полином в числителе может быть представлен в виде, то (27) преобразуется к виду:

.

Пример 15. Необходимо определить выражение для решетчатой функции , если

.

Используя (30), имеем:

Рассчитанные по полученному выражению значения дискрет, как и следовало ожидать, совпадают с вычисленными в предыдущем примере.

Если все условия, ограничивающие применение (30), выполняются, за исключением того, что полином не имеет нулевого корня, то искомая решетчатая функция определяется по формуле:

,

которую можно использовать для . При этом величинуследует находить по теореме о начальном значении.

Пример 16. Необходимо определить выражение для решетчатой функции, если

.

Начальное значение решетчатой функции равно:

.

Для определения предыдущих значений по (31) полагаем:

В соответствии с полученным выражением для имеем:

;и т.д.

Если число нулей равно числу полюсов (25) (порядок полиномов иравны), следует, разделивна, представитьв виде суммы составляющей нулевого порядка и дробно-рационального остатка. При этом первое слагаемое определяет величину, а по второму, используя формулу (31), можно вычислить искомую решетчатую функцию.

Пример 17. Необходимо определить выражение для решетчатой переходной функции разомкнутой дискретной САУ, передаточная функция ПНЧ которой равна:

Передаточная функция дискретной системы:

.

Z– изображение переходной функции:

.

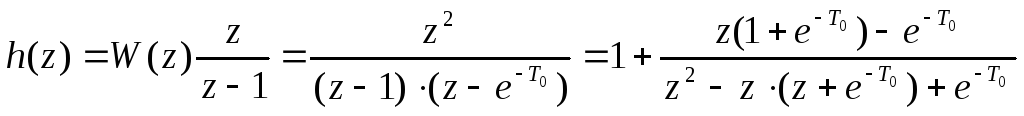В соответствии с формулой (31) можно записать:

;

;

Начальное значение решетчатой функции: . Длясправедливо:

.
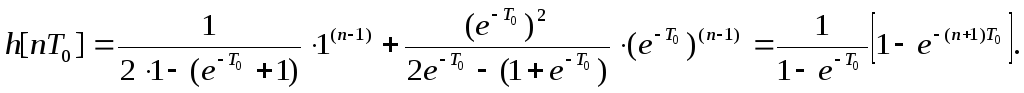