Файл: Г.М. Гринфельд лекции по курсу дискретные системы автоматического управления.doc

Следуя рассмотренной выше методике, необходимо, в первую очередь, найти решетчатую функцию, соответствующую . Выполнение этой операции сводится к формальной замене непрерывного аргументаtв функциина дискретное время. В рассматриваемом примере:

.

Следующий этап – нахождение дискретного преобразования Лапласа приведенной решетчатой функции. С учетом (11) имеем:

.

Применяя формулу суммы членов бесконечно убывающей прогрессии, получаем:

.

Переход к Z– изображению осуществляем на основании (13):

. (14)

Пример 4. Необходимо найти Z-преобразование выходного сигнала ПИЭ, входной сигнал которого – единичная ступенчатая функция. Искомое изображение определим непосредственно по формуле (12):

(15)

Аналогичный результат может быть получен, если в (14) перейти к пределу при .

Пример 5. Необходимо найти Z-преобразование функции.

Соответствующая решетчатая функция . На основании (12) имеем:

.

Умножая обе части этого выражения на , получим:

.

Вычтем последнее выражение из предыдущего:

.

Следовательно

. (16)

Рассмотрим иной метод выполнения Z-преобразования, который предполагает использование непрерывногоL-изображения сигналавместо решетчатой функциии ееD-изображения. Для случая, когда изображениеимеет конечное число простых полюсов, оно может быть представлено в виде:

,

где p – i-й простой полюс изображения;k– порядок полинома

Осуществим замену и преобразуем последнее выражение к виду:

(17)

Пример 6. Используя формулу (17), необходимо найти Z-изображение экспоненциального сигнала (см. пример 3) непосредственно по егоL- изображению.

Зная, что

,

можно записать:

Тогда

Как и следовало ожидать, полученный результат совпадает с (14).

Согласно (12) определяется только величинами дискрет решетчатой функциии абсолютно не учитывает поведение непрерывного сигналамежду моментами квантования. Тем не менее, для обозначения операцииZ-преобразования наряду св дальнейшем используются выражения видаили. Эта формальная запись означает только то, чтоZ-преобразование осуществляется по решетчатой функции, полученной путем квантования непрерывного сигнала, обладающегоL-изображением.

Для наиболее часто встречающихся функций существуют таблицыZ-изображений, достаточно подробные таблицы приведены в [2,11].

2.2. Основные теоремы z-преобразования.

Математический аппарат Z-преобразования является основой теории дискретных САУ. Ниже приведены формулировки основных теоремZ-преобразования и примеры их применения.

1. Теорема о линейности преобразования:

Если константы, то

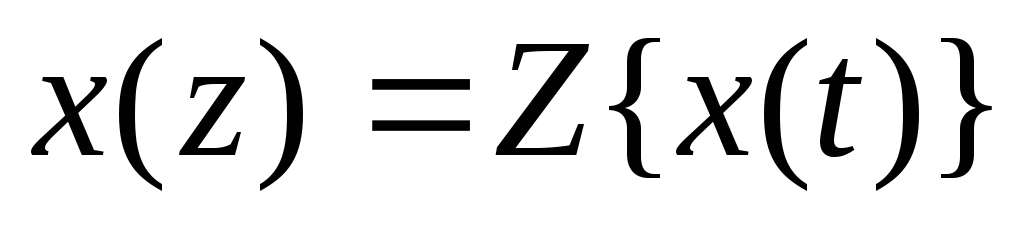2. Теорема о смещении во временной области:

Если , а k-натуральное число, то

.

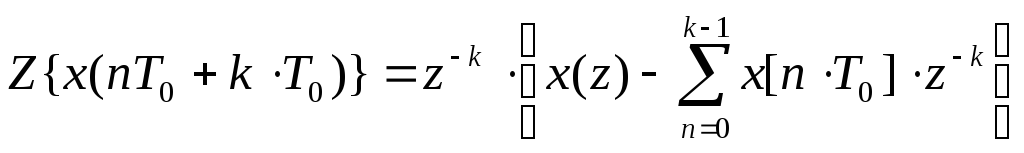
3. Теорема об умножении оригинала на экспоненту:

Есликонстанта, то

.

4. Теорема о начальном значении:

Если и существует предел , то

.

5. Теорема о конечном значении:

Если и если функция не имеет полюсов на окружности единичного радиуса и вне ее на комплексной плоскостиZ, то

.

Пример 7. Необходимо найти Z-изображение функции.

На основании теоремы линейности можно записать:

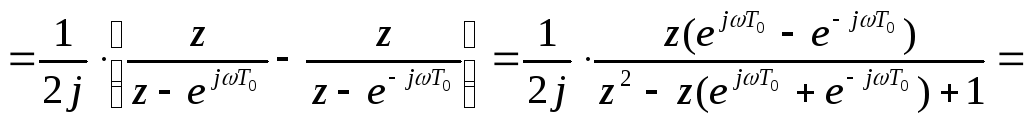
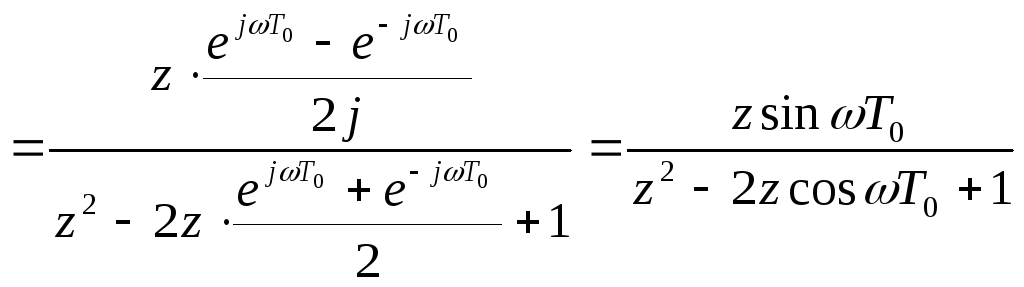
Пример 8. Необходимо найти Z-изображение функции.

Используя теорему об умножении на экспоненту применительно к (16), можно записать

.

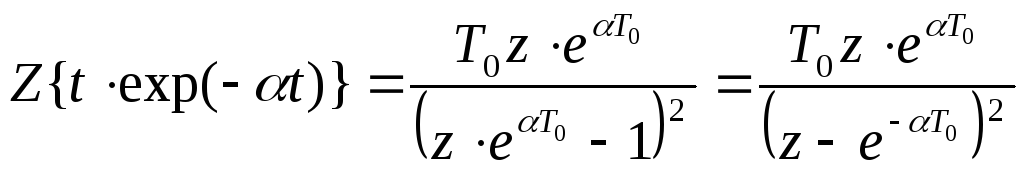2.3. Передаточная функция разомкнутой дискретной системы.

По аналогии с непрерывными системами введем в рассмотрение передаточную функцию дискретной системы , как отношениеZ- изображений выходного и входного сигналов при нулевых начальных условиях:

. (18)

В разомкнутой дискретной САУ (рис. 13) сигналы и- непрерывные функции времени, и формула (19) определяет связь не между ними, а между соответствующими решетчатыми функциямии.

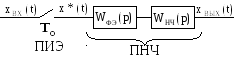
Рис.13. К определению дискретной

передаточной функции

Как было указано выше, рассматриваемые выше в данном курсе импульсные САУ с АИМ и , являются линейными. В линейных системах, как в непрерывных, так и в дискретных, передаточная функция не зависит от вида входного сигнала. Поэтому с целью упрощения вывода формул дляв качестве входного сигнала используется единичный одиночный импульс, который описывается зависимостью:

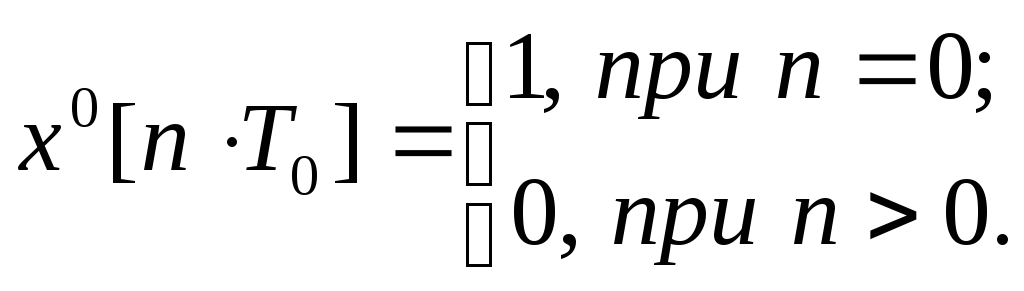
Z-изображение такого сигнала равно единице. На выходе квантователя ему будет соответствовать немодулированная- функция. Следовательно, реакция САУ на единичный одиночный импульс является функция веса ПНЧ, а ееZ-изображение совпадает с передаточной функцией: