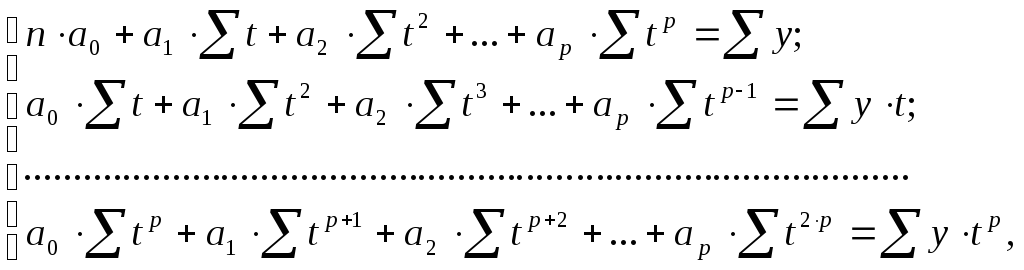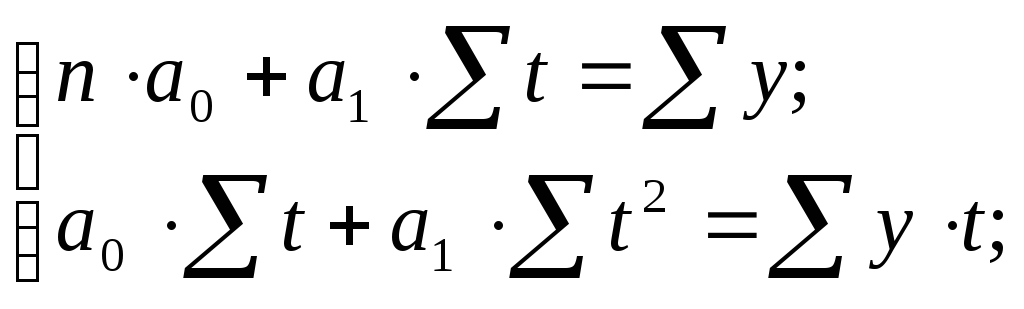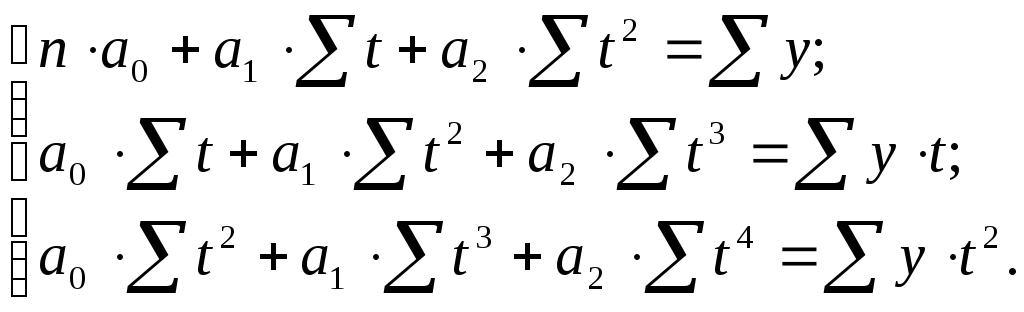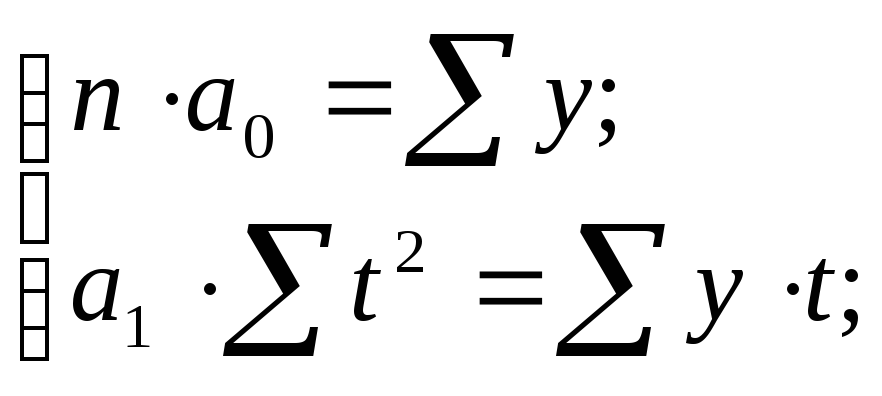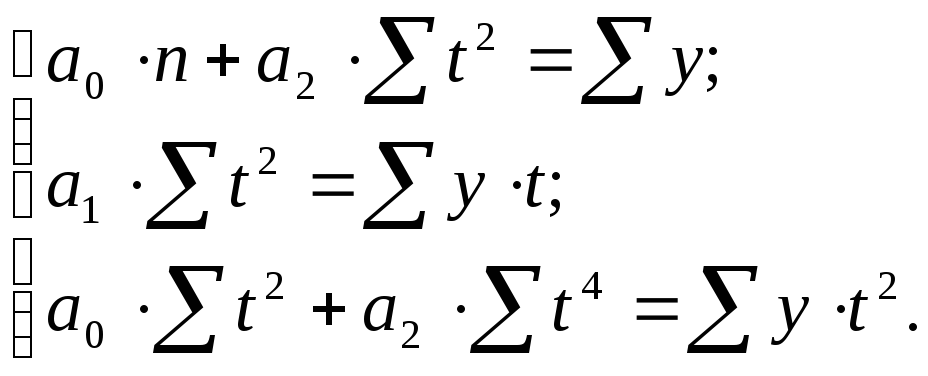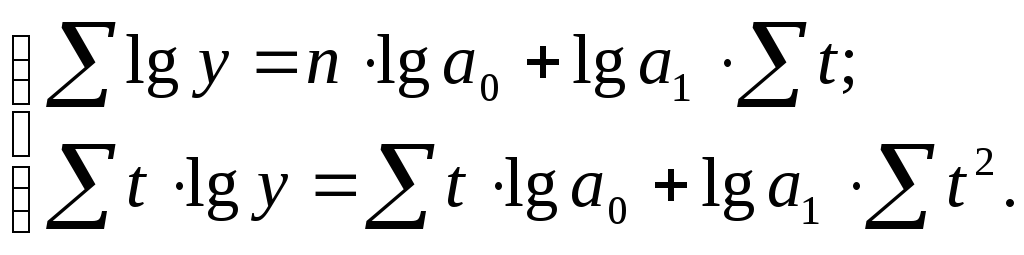Файл: Тема 10.doc

Отсюда находятся методом наименьших квадратов, сущность которого нам известна из регрессионного анализа.

Согласно этому методу для нахождения параметров полинома -й степени необходимо решить систему так называемых нормальных уравнений:

Система (10.32), состоящая из уравнений, содержит в качестве известных величины,, …,, т.е. суммы наблюдаемых значений уровней динамического ряда, умноженные на показатели времени в степени, и-неизвестных величин. Решение этой системы относительно и дает искомые значения параметров.

Системы для расчета параметров полиномов невысоких степеней намного проще. Обозначим последовательные параметры полиномов как . Тогда системы нормальных уравнений для оценивания параметров прямой () примут вид:

для параболы 2-го порядка ():

Решение системы (10.33) относительно искомых параметров и:

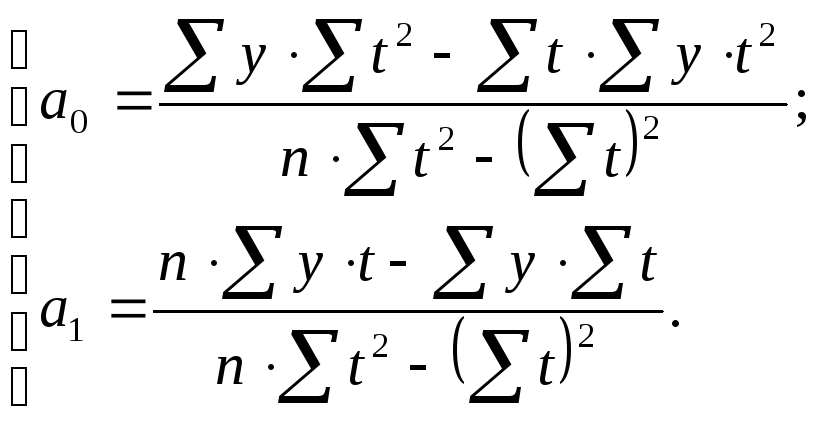
Аналогичным путем можно было бы подойти и к системе (10.34). Однако такой путь расчета параметров достаточно трудоемок, если он не выполняется с помощью пакета прикладных программ. Поэтому перейдем к упрощенным приемам расчета параметров, применение которых дает ощутимую экономию труда без какой-либо потери точности результатов.

Упрощенный расчет параметров уравнений заключается в переносе начала координат в середину ряда динамики. В этом случае упрощаются сами нормальные уравнения, кроме того, уменьшаются абсолютные значения величин, участвующих в расчете. В самом деле, если до переноса начала координат было равно, то после переноса, если число членов ряда нечетное. Когда же число ряда четное, то. Следовательно,и все, у которых- нечетное число, равны 0. Таким образом, все члены уравнений, содержащиес такими степенями, могут быть исключены. Системы нормальных уравнений теперь упрощаются для прямой:

для параболы второго порядка:

Решая системы (10.35), (10.36) относительно неизвестных параметров, получим величины параметров соответствующих полиномов.

Параметр выражает начальную скорость роста, а коэффициент - постоянную скорость изменения прироста. Если уровень явления растет с ускорением, то величина этого ускорения в среднем за изучаемый период равна единицам.

При сглаживании ряда динамики по экспоненте для определения параметров применяется метод наименьших квадратов к логарифмам исходных данных. Так, для нахождения параметров экспоненты необходимо решить следующую систему уравнений:

Если , то параметры уравнения и находим по формулам:

;.

Экспонента отражает постоянный относительный рост, равный единицам.

Во многих случаях моделирование рядов динамики с помощью полиномов или экспоненциальной функции не дает удовлетворительных результатов, так как в рядах динамики содержатся заметные периодические колебания вокруг общей тенденции или наблюдается автокорреляция не в самих уровнях, а в их отклонениях от теоретических значений, полученных по определенным аналитическим формулам. В таких случаях следует использовать гармонический анализ.

Целью данного анализа являются выявление и измерение периодических колебаний в рядах динамики и автокорреляции в остатках ряда.

Функцию, заданную в каждой точке изучаемого интервала времени, можно представить бесконечным рядом синусоидальных и косинусоидальных функций. Нахождение конечной суммы уровней с использованием функций косинусов и синусов времени называется гармоническим анализом.

Другими словами, гармонический анализ представляет собой операцию по выражению заданной периодической функции в виде ряда Фурье по гармоникам разных порядков. Каждый член ряда представляет собой слагаемое постоянной величины с функциями косинусов и синусов определенного периода.

В простейшем случае динамика явлений, обладающих периодичностью, может быть аппроксимирована синусоидой:

При получаем.

Аппроксимация динамики экономических явлений рядом Фурье состоит в выборе таких гармонических колебаний, наложение которых друг на друга (сумма) отразит периодические колебания фактических уровней динамического ряда. С помощью ряда Фурье можно представить динамику явлений в виде некоторой функции времени, в которой слагаемые расположены по убыванию периодов:

В этом уравнении величина определяет гармонику ряда Фурье и может быть взята целым числом (чаще всего от 1 до 4). Параметры уравнения рассчитываются методом наименьших квадратов.

Найдя частные производные этой функции и приравняв их к нулю, получим систему нормальных уравнений, из которой вычислим параметры:

;;.

Последовательные значения обычно определяются от 0 с увеличением (приростом), равным, где - число уровней ряда динамики.

Для изучения специфического периодического явления - сезонности берется , по числу месяцев в году.

Тогда ряд динамики годового производства можно записать так:

;;;;;;;;;;;.

;;;;;;;;;;;.