ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.08.2024
Просмотров: 122
Скачиваний: 0
СОДЕРЖАНИЕ
Тема 7 показатели вариации и анализ частотных распределений
Вариация признака в совокупности и значение ее изучения
7.2 Показатели центрараспределения
7.3 Показатели вариации и способы их расчета
7.4 Вариации альтернативного признака. Энтропия распределения
7.5 Виды дисперсий в совокупности, разделенной на группы. Правило сложения дисперсий
7.6 Структурные характеристики вариационного ряда распределения. Показатели дифференциации
7.8 Изучение формы распределения
7.9 Теоретические распределения в анализе вариационных рядов
Таким образом, анализируя формулы моментов распределения в табл. 7.14, можно сделать следующие выводы:
начальный момент первого порядка представляет собой среднюю арифметическую и используется как показатель центра распределения (
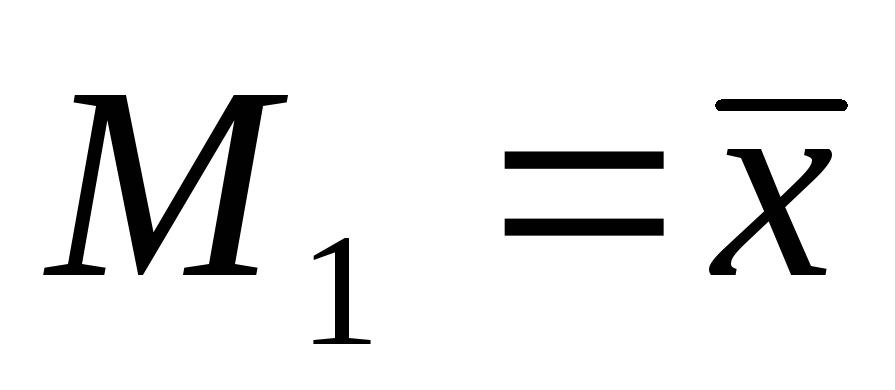 );
);начальные моменты 2-го, 3-го и 4-го порядков не имеют самостоятельного значения, а используются для упрощения вычислений центральных моментов. Например, используя начальные моменты 1-го и 2-го порядка, можно получить дисперсию по такой формуле:
|
|
(7.67) |
центральный момент 1-го порядка всегда равен нулю в соответствии с нулевым свойством средней арифметической (
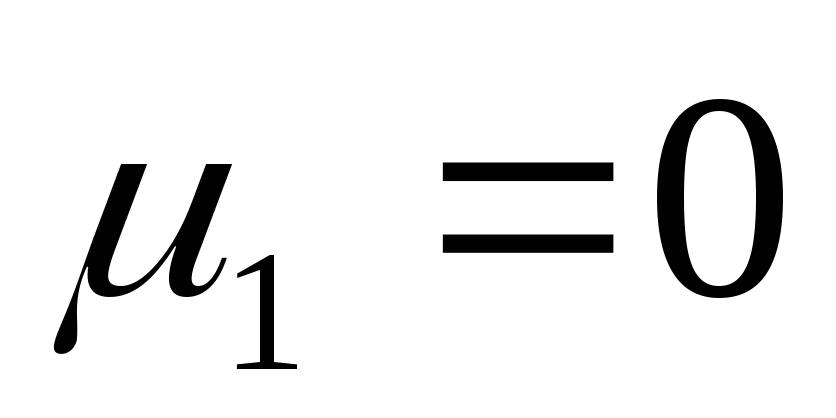 );
);центральный момент 2-го порядка представляет собой дисперсию и служит основной мерой колеблемости признака (
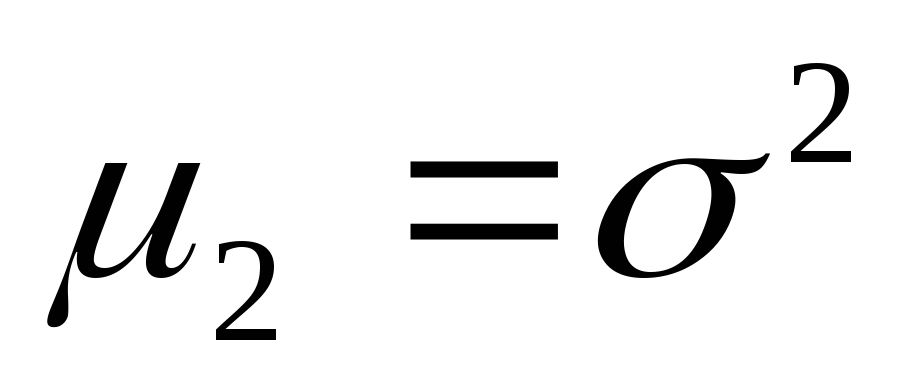 );
);центральный момент 3-го порядка служит мерой асимметрии распределения, а если распределение симметрично, он равен нулю(
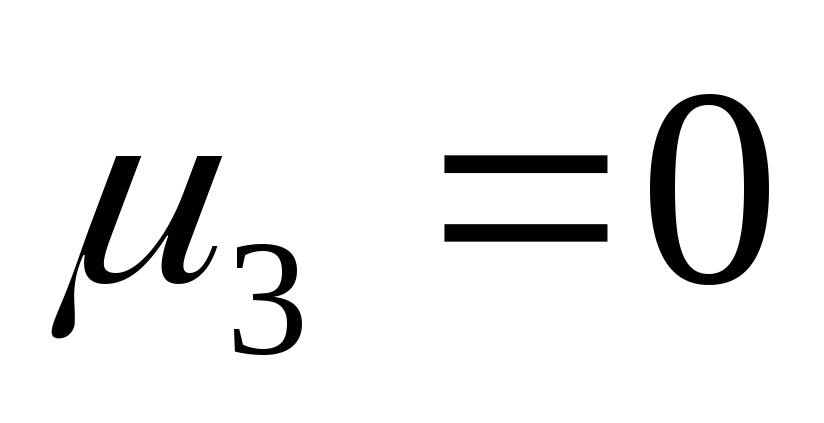 );
);центральный момент четвертого порядка применяется при вычислении показателя эксцесса;
условные моменты 1-го, 2-го, 3-го и 4-го порядков не имеют самостоятельного значения, а используются для упрощения вычислений центральных моментов.
7.8 Изучение формы распределения
Для обобщающей характеристики особенностей формы распределения применяются кривые распределения. Кривая распределения выражает графически (полигон, гистограмма) закономерность распределения единиц совокупности по величине варьирующего признака. Различают эмпирические и теоретические кривые распределения.Эмпирическая кривая распределения - это фактическая кривая распределения, полученная по данным наблюдения, в которой отражаются как общие, так и случайные условия, определяющие распределение.Теоретическая кривая распределения - это кривая, выражающая функциональную связь между изменением варьирующего признака и изменением частот и характеризующая определенный тип распределения. При этом теоретическое распределение играет роль некоторой идеализированной модели эмпирического распределения, а сам анализ вариационного ряда сводится к сопоставлению эмпирического и теоретического распределений.
Кривые распределения бывают симметричными и асимметричными. В зависимости от того, какая ветвь кривой вытянута - правая или левая, различают правостороннюю или левостороннюю асимметрию. Кривые распределения могут быть одно-, двух- и многовершинными.
Для однородных совокупностей, как
правило, характерны одновершинные
распределения. Многовершинность
свидетельствует о неоднородности
изучаемой совокупности. Появление двух
и более вершин делает необходимой
перегруппировку данных с целью выделения
более однородных групп. Для симметричных
распределений частоты любых двух
вариант, равноотстоящих в обе стороны
от центра, равны между собой. Рассчитанные
для таких рядов распределений
характеристики равны:
![]() ,
,![]() ;
;![]() .
Если указанные соотношения нарушены,
то это свидетельствует о наличии
асимметрии распределения. Так, при
.
Если указанные соотношения нарушены,
то это свидетельствует о наличии
асимметрии распределения. Так, при![]() разности между
разности между![]() и
и![]() положительные и асимметрия правосторонняя,
а при
положительные и асимметрия правосторонняя,
а при![]() ,
наоборот, разности
,
наоборот, разности![]() и
и![]() отрицательные и асимметрия левосторонняя.
отрицательные и асимметрия левосторонняя.
При сравнительном изучении асимметрии
нескольких распределений с разными
единицами измерения вычисляется
относительный показатель асимметрии
(![]() ):
):
|
|
(7.68) |
Его величина может быть положительной и отрицательной. В первом случае речь идет о правосторонней асимметрии, а во втором - о левосторонней (рис. 7.4).

В симметричном распределении центральный
момент 3-го порядка
![]() ,
поэтому чем он больше, тем больше и
асимметрия. Эта особенность и используется
для характеристики асимметрии.Коэффициент
асимметрии равен отношению центрального
момента 3-го порядка к среднему
квадратическому отклонению в кубе, т.е.
,
поэтому чем он больше, тем больше и
асимметрия. Эта особенность и используется
для характеристики асимметрии.Коэффициент
асимметрии равен отношению центрального
момента 3-го порядка к среднему
квадратическому отклонению в кубе, т.е.
|
|
(7.69) |
Если
![]() ,
то асимметрия правосторонняя, а если
,
то асимметрия правосторонняя, а если
![]() ,
то асимметрия левосторонняя. Чем
числитель ближе к 0, тем асимметрия
меньше. Этот показатель асимметрии
более точен по сравнению с предыдущими
и применяется более широко. Принято
считать, что асимметрия выше 0,5 (независимо
от знака) считается значительной; если
она меньше 0,25, то незначительной.
,
то асимметрия левосторонняя. Чем
числитель ближе к 0, тем асимметрия
меньше. Этот показатель асимметрии
более точен по сравнению с предыдущими
и применяется более широко. Принято
считать, что асимметрия выше 0,5 (независимо
от знака) считается значительной; если
она меньше 0,25, то незначительной.
Оценка существенности
![]() проводится на основе средней квадратической
ошибки, коэффициента асимметрии
проводится на основе средней квадратической
ошибки, коэффициента асимметрии![]() ,
которая зависит от числа наблюдений
(
,
которая зависит от числа наблюдений
(![]() )
и рассчитывается по формуле:
)
и рассчитывается по формуле:
|
|
(7.70) |
В случае
![]() асимметрия существенна и распределение
признака в генеральной совокупности
несимметрично. В противном случае
асимметрия несущественна и ее наличие
может быть вызвано случайными
обстоятельствами.
асимметрия существенна и распределение
признака в генеральной совокупности
несимметрично. В противном случае
асимметрия несущественна и ее наличие
может быть вызвано случайными
обстоятельствами.
Для симметричных распределений может
быть рассчитан показатель эксцесса
(![]() ).
Наиболее точно он определяется по
формуле с использованием центрального
момента 4-го порядка
).
Наиболее точно он определяется по
формуле с использованием центрального
момента 4-го порядка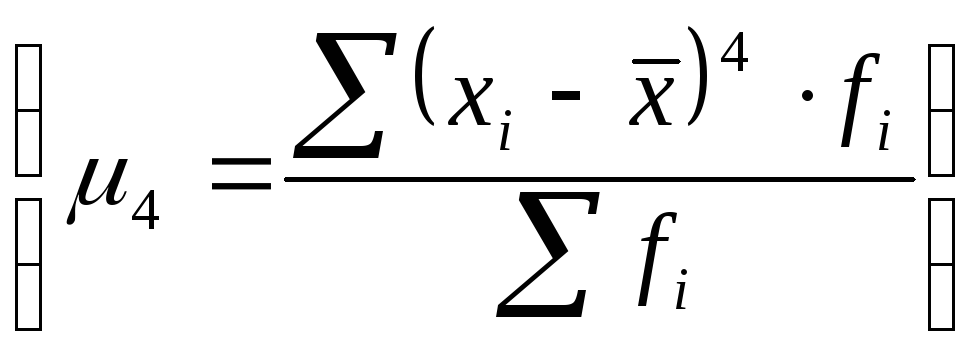 :
:
|
|
(7.71) |
На рис. 7.5 и 7.6 представлены два
распределения: островершинное (Ек
положительный) и плосковершинное (![]() отрицательный). В нормальном распределении
отрицательный). В нормальном распределении![]() .
.
Среднеквадратическая ошибка эксцесса
(![]() )
рассчитывается по формуле:
)
рассчитывается по формуле:
|
|
(7.72) |
где
![]() - число наблюдений.
- число наблюдений.
Для определения асимметрии и эксцесса можно пользоваться упрощенными формулами, предложенными Линдбергом:
|
|
(7.73) |
где
![]() - удельный вес (%) количества тех
вариант, которые превосходят среднюю
арифметическую, в общем количестве
вариант данного ряда;
- удельный вес (%) количества тех
вариант, которые превосходят среднюю
арифметическую, в общем количестве
вариант данного ряда;
50 - удельный вес (%) вариант, превосходящих среднюю арифметическую ряда нормального распределения.
|
|
(7.74) |
где
![]() - доля (%) количества вариант, лежащих
в интервале, равном половине среднего
квадратического отклонения (в ту или
другую сторону от величины средней в
общем количестве вариант данного ряда);
- доля (%) количества вариант, лежащих
в интервале, равном половине среднего
квадратического отклонения (в ту или
другую сторону от величины средней в
общем количестве вариант данного ряда);
38,29 - доля (%) количества вариант, лежащих в интервале, равном половине среднего квадратического отклонения (в ту или другую сторону от величины средней), в общем количестве вариант ряда нормального распределения.
Необходимо отметить, что хотя показатели асимметрии и эксцесса характеризуют непосредственно лишь форму распределения признака в пределах изучаемой совокупности, однако их определение имеет не только описательное значение. Часто асимметрия и эксцесс дают определенные указания для дальнейшего исследования социально-экономических явлений. Например, появление значительного отрицательного эксцесса может указывать на качественную неоднородность исследуемой совокупности. Кроме того, эти показатели позволяют сделать вывод о возможности отнесения данного эмпирического распределения к типу кривых нормального распределения.