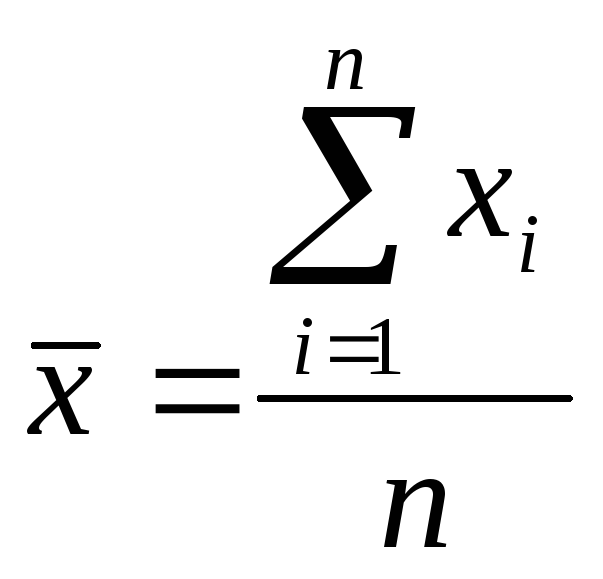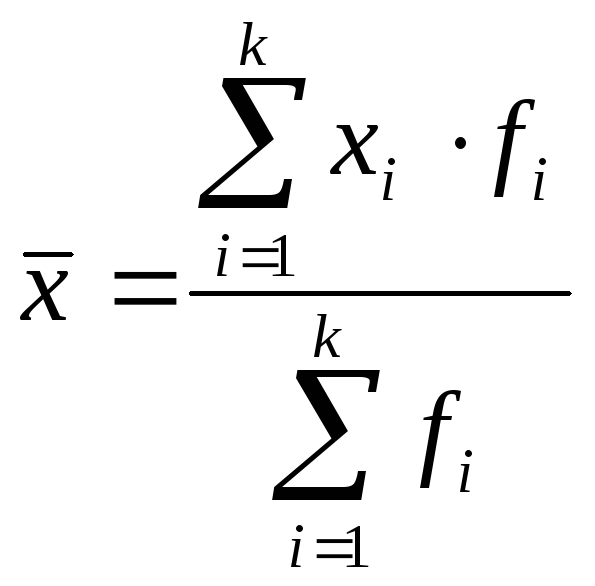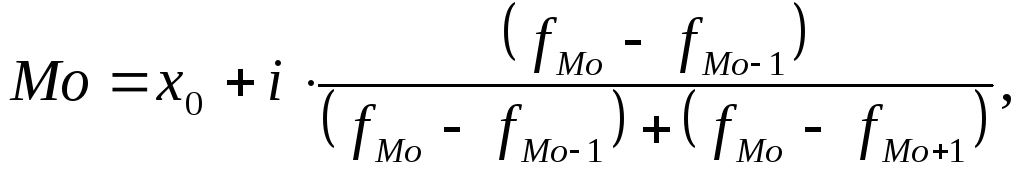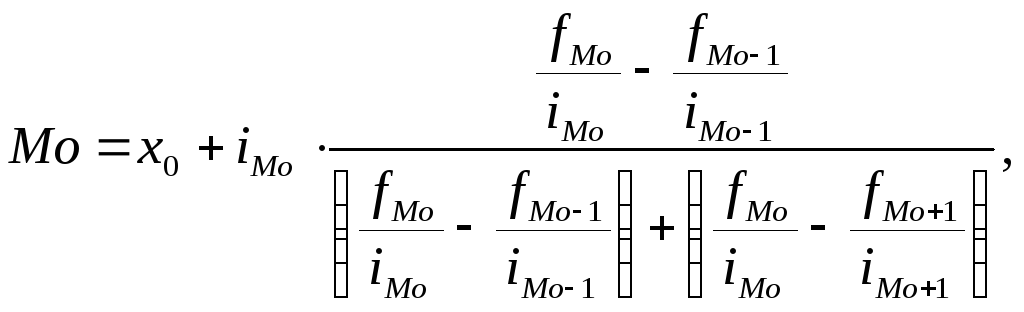Файл: Тема 7.doc

При изучении социально-экономических явлений и процессов статистика встречается с разнообразной вариацией признаков, характеризующих отдельные единицы совокупности. Величины признаков колеблются, варьируют под действием различных причин и условий, которые в статистике называются факторами. Нередко эти факторы действуют в противоположных направлениях и сами, в свою очередь, варьируют. Среди них есть существенные факторы, определяющие величину вариантов данного признака у всех единиц совокупности. Но есть и несущественные (чисто случайные), которые на одни единицы совокупности могут оказывать влияние, на другие нет. Например, вариация оценок студентов на экзамене в вузе вызывается, в частности, различными способностями студентов; временем, затраченным ими на самостоятельную работу; посещаемостью занятий; различием социально-бытовых условий и т.д. Но на оценку могут влиять и какие-либо привходящие, чисто случайные причины, например, временное недомогание. Вариация, порождаемая существенными факторами, носит систематический характер, т.е. наблюдается последовательное изменение вариантов признака в определенном направлении. Такая вариация называетсясистематической. В систематической вариации проявляются взаимосвязи между явлениями, их признаками, в такой связи - один как причина (фактор), другой как следствие (результат) его действия. Точнее говоря, проявляется зависимость вариации одного признака от вариации другого или от нескольких других.

Вариация, обусловленная случайными факторами, называется случайной вариацией. Здесь не наблюдается систематического изменения вариантов зависимого признака от случайных факторов; все изменения носят хаотический характер, поскольку нет устойчивой связи этих факторов с единицами изучаемой совокупности.

Вариация зависимого признака, образовавшаяся под действием всех без исключения влияющих на него факторов, называется общей вариацией. Следовательно, общая вариация слагается из систематической и случайной вариации. Но систематическая вариация, если между признаками имеется довольно существенная связь, в конце концов пробивает себе дорогу через хаос случайных колебаний вариантов зависимого признака и проявляет себя.

Наличие вариации признаков, изучаемых статистикой явлений, ставит задачу определить меру вариации, ее измерение, найти соответствующие измерители - показатели, характеризующие размеры этой вариации, а также выявить сущность и методы вычисления определяющих ее факторов.

По степени вариации изучаемые явления можно рассматривать с различных аспектов, в частности, судить об однородности совокупности, устойчивости индивидуальных значений признака, типичности средней, о взаимосвязи между признаками одного и того же явления и признаками разных явлений. Статистические показатели, характеризующие вариацию, широко применяются в практической деятельности, например для оценки ритмичности работы промышленных предприятий, используются как контроль над производственными процессами, а также для определения устойчивости урожайности сельскохозяйственных культур тех или иных сортов или одного и того же сорта в определенных климатических условиях. На основе вариации в статистике разрабатываются показатели, характеризующие социально-экономические явления и процессы, например показатели тесноты связи между явлениями и их признаками, показатели оценки точности выборочного наблюдения.

В данной теме в основном рассматриваются приемы изучения случайной вариации, т.е. вариации количественного признака в однородной совокупности. Совокупность значений изучаемого признака с указанием числа различных значений называетсяраспределением признака. Распределение представляют в видевариационного ряда.

Каким же образом статистика дает количественную оценку степени колеблемости признака в совокупности, измеряет вариацию?

Для характеристики закономерностей распределения изучаемого признака недостаточно пользоваться только вариационными рядами распределения и их графическим изображением. В процессе анализа требуется вычислить различные числовые характеристики (показатели), которые в обобщенном виде отразят особенности распределения изучаемых признаков. Наличие таких характеристик (показателей) существенно облегчаетсравнение различных распределений между собой.

Все показатели вариации в зависимости от характеризуемых ими особенностей можно разделить на три группы:

показатели центра распределения - средняя арифметическая, мода и медиана;
показатели степени вариации - вариационный размах, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение и коэффициент вариации;
показатели типа (формы) распределения - структурные характеристики, показатели асимметрии и эксцесса, кривые распределения.

7.2 Показатели центрараспределения

Важнейшей характеристикой центра распределения является средняя арифметическая (). Для вычисления по даннымпервичного ряда применяется формула простой средней арифметической.

(7.1)

При вычислении по данным ранжированного вариационного ряда применяется формула средней взвешенной:

(7.2)

В отличие от средней арифметической, рассчитываемой на основе использования всех вариантов значений признака, мода и медиана характеризуют величину варианта, занимающего определенное положение в ранжированном вариационном ряду.

Модой распределения () называется такая величина изучаемого признака, которая в данной совокупности встречается наиболее часто, т.е. один из вариантов признака повторяется чаще, чем все другие.

Для упорядоченного дискретного ряда распределения мода, являющаяся характеристикой вариационного ряда, определяется по частотам вариантов и соответствуетварианту с наибольшей частотой.

Модальный интервал (т.е. содержащий моду) в случае интервального распределения с равными интервалами определяется по наибольшей частоте; с неравными интервалами - по наибольшей плотности, а определение моды требует проведения расчетов на основе следующих формул:

(7.3)

где - нижняя граница модального интервала;

- величина модального интервала;

- частота модального интервала;

- частота интервала, предшествующего модальному;

- частота интервала, следующего за модальным;

(7.4)

где - начальная граница модального интервала, в котором достигает максимума величина- отношение частоты интервала к его величине;

,,- величина соответствующего модального, до- и послемодального интервалов;

,,- частота модального, до- и послемодального интервалов соответственно.

В качестве характеристик вариационного ряда также применяется медиана (), т.е. величина изучаемого признака, которая находится в середине упорядоченного вариационного ряда. Главное свойство медианы в том, чтосумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины:

(7.5)

Если в вариационном ряду случаев, то значение признака у случаябудет медианным. Если в ряду четное число случаев, то медиана равна средней арифметической из двух данных значений.