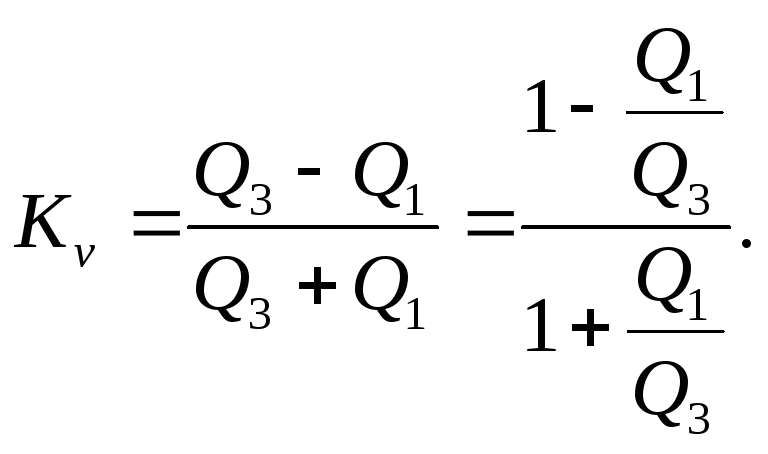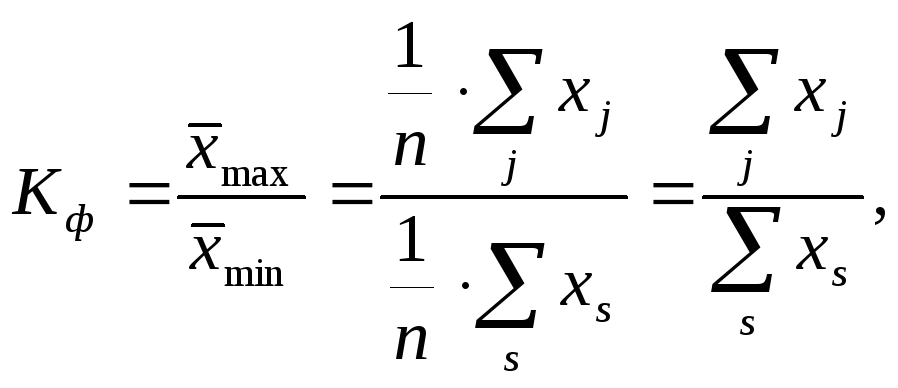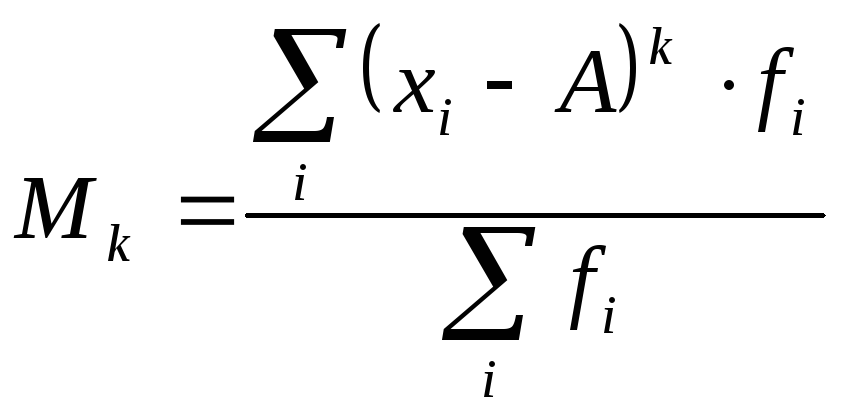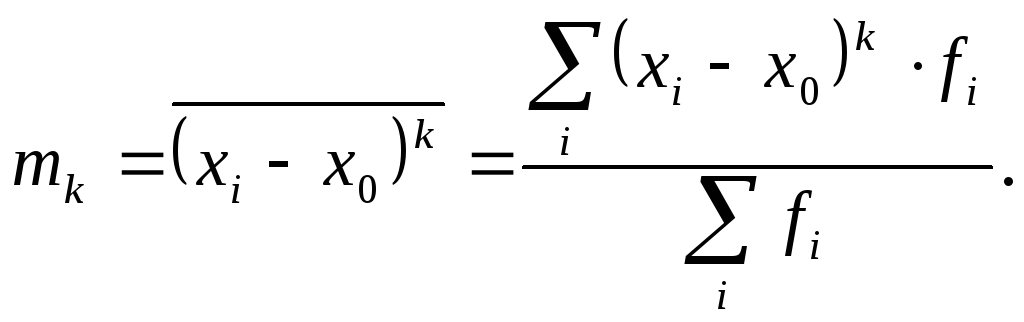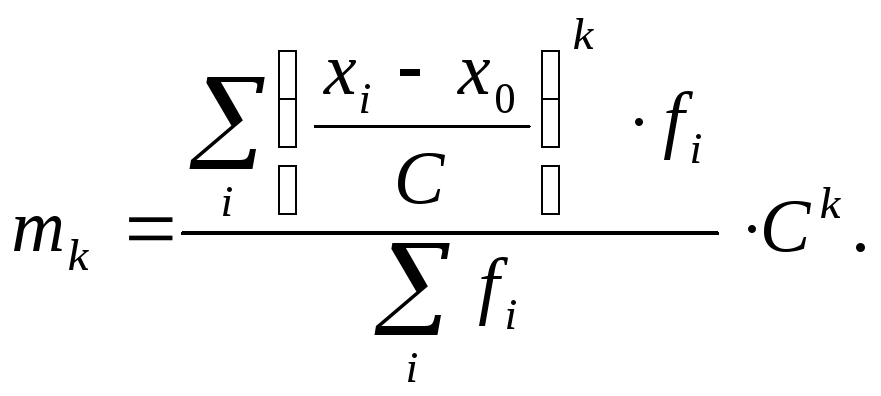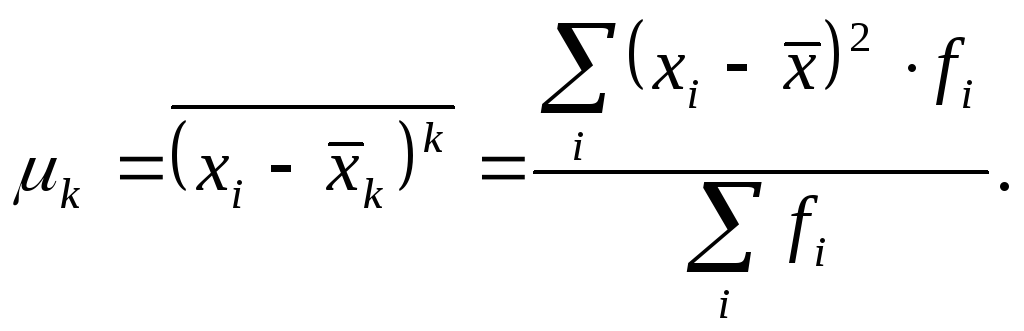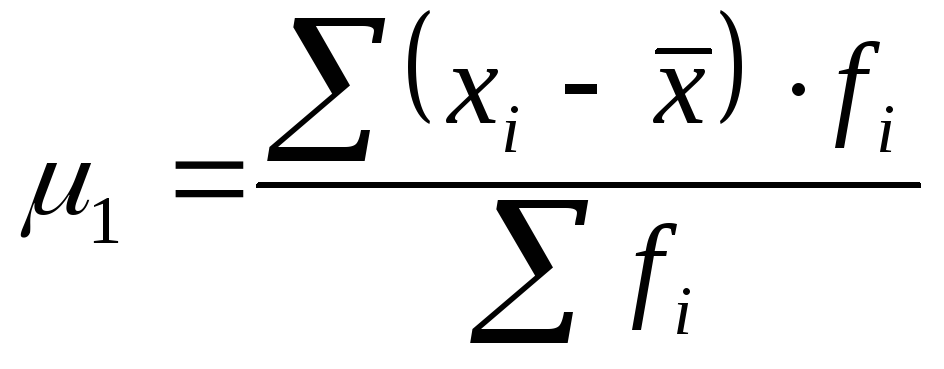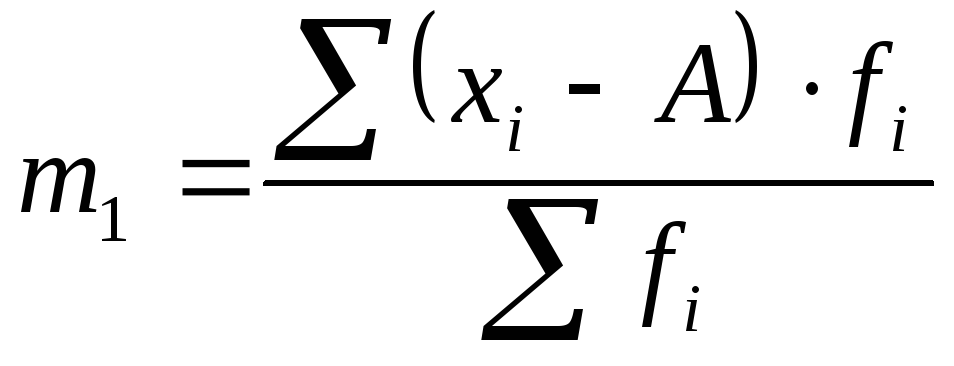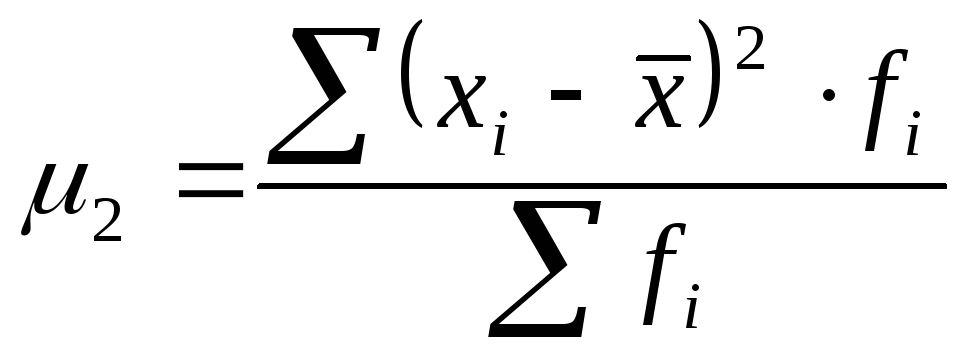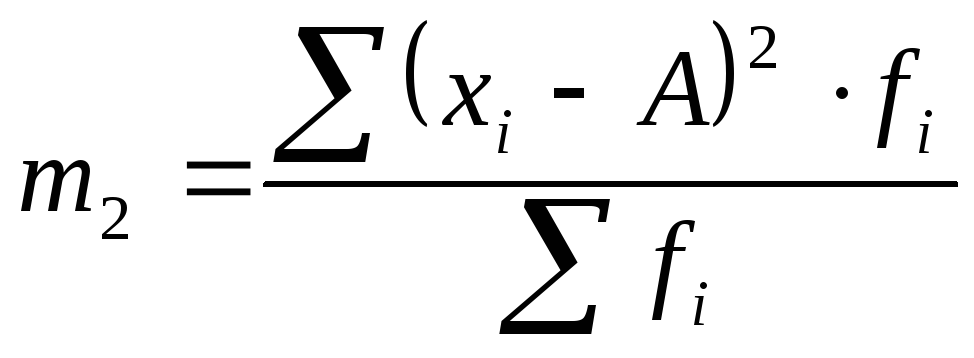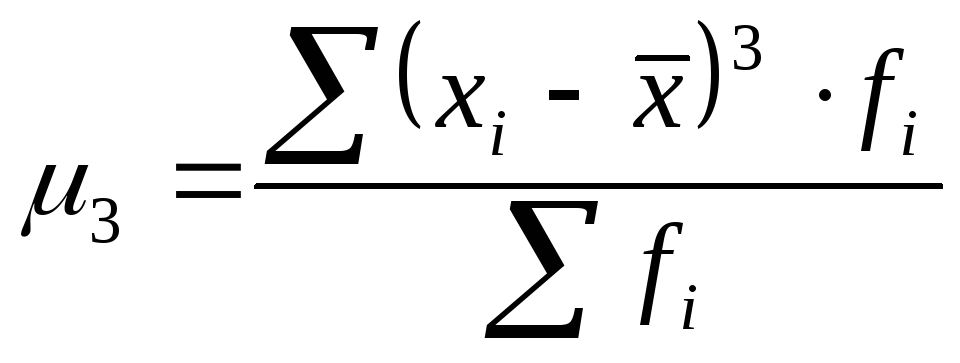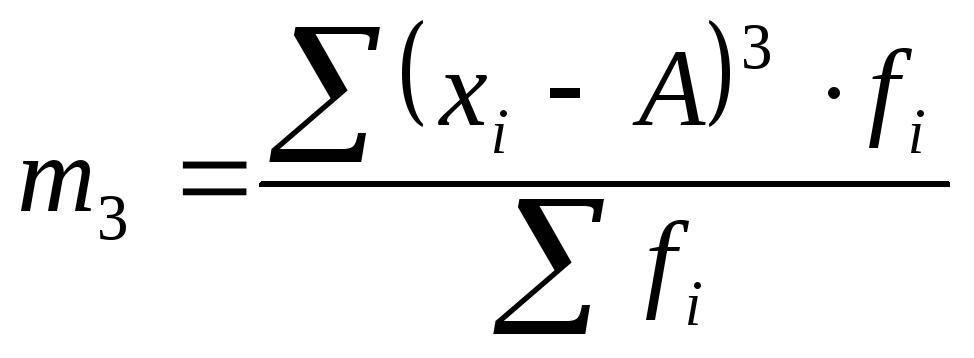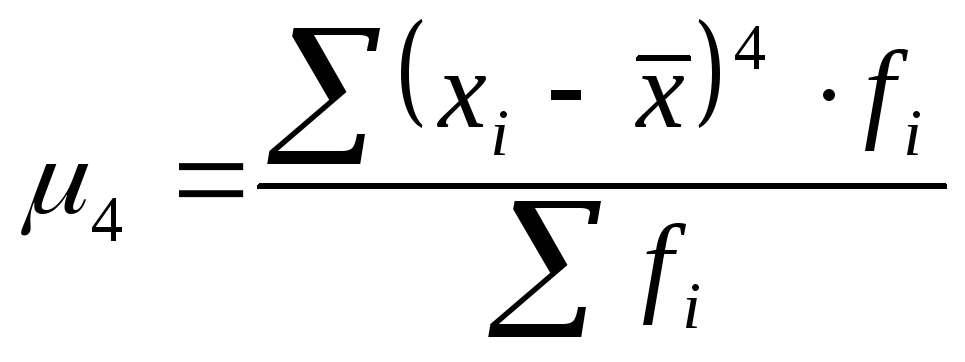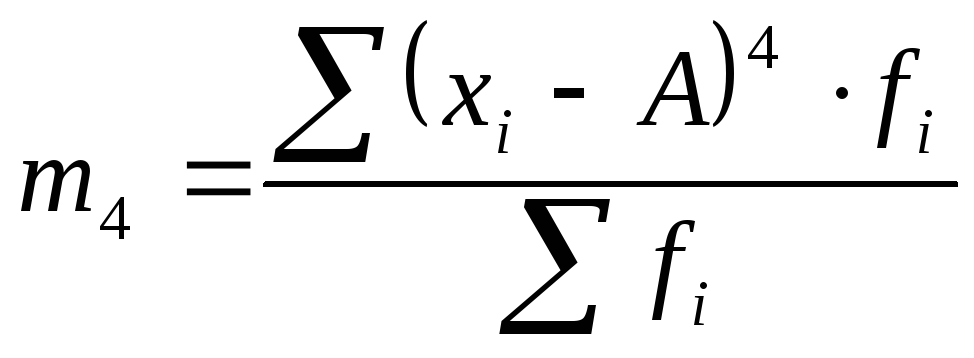ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.08.2024
Просмотров: 125
Скачиваний: 0
СОДЕРЖАНИЕ
Тема 7 показатели вариации и анализ частотных распределений
Вариация признака в совокупности и значение ее изучения
7.2 Показатели центрараспределения
7.3 Показатели вариации и способы их расчета
7.4 Вариации альтернативного признака. Энтропия распределения
7.5 Виды дисперсий в совокупности, разделенной на группы. Правило сложения дисперсий
7.6 Структурные характеристики вариационного ряда распределения. Показатели дифференциации
7.8 Изучение формы распределения
7.9 Теоретические распределения в анализе вариационных рядов
Значения признака, делящие ряд распределения на сто частей, называются перцентилями. Слово «перцентиль» относится непосредственно к элементу распределения или к значению, промежуточному между двумя элементами. Для того чтобы указать местоположение конкретного наблюдения, в распределении указывается так называемыйперцентильный ранг; он равен сумме процентов, приходящихся на наблюдения, которые в распределении стоят ниже его, и половине процентов, которые приходятся на него непосредственно.
Метод нахождения перцентилей можно представить с помощью следующей формулы:
|
|
(7.56) |
где
![]() - обозначение
- обозначение![]() -го
перцентиля;
-го
перцентиля;
![]() - нижняя граница интервала;
- нижняя граница интервала;
![]() - число оценок, необходимое попасть в
точку на горизонтальной оси, которая
соответствует данному перцентилю;
- число оценок, необходимое попасть в
точку на горизонтальной оси, которая
соответствует данному перцентилю;
![]() - расстояние от нижней границы
- расстояние от нижней границы![]() до верхней границы
до верхней границы![]() (шаг интервала);
(шаг интервала);
![]() - число оценок, расположенных в интервале
от
- число оценок, расположенных в интервале
от![]() до
до![]() .
.
Рассмотренные показатели можно представить в следующем соотношении (рис. 7.3).
Использование в анализе вариационных рядов распределения рассмотренных выше характеристик позволяет глубоко и детально охарактеризовать изучаемую совокупность.
Показатели дифференциации. В тех
случаях, когда при изучении вариационного
ряда возникает необходимость дать
относительную характеристику степени
вариации ряда и имеются уже предварительно
вычисленные квартили и децили, то можно
вычислить коэффициент дифференциации
(![]() ).
).
В зависимости от заданных ранговых показателей коэффициенты дифференциации рассчитываются по-разному.
Если заданы 3-я (
 )
и 1-я (
)
и 1-я ( )
квартили, то вместо коэффициента
вариации (
)
квартили, то вместо коэффициента
вариации ( )
можно вычислитькоэффициент
дифференциации по формуле
)
можно вычислитькоэффициент
дифференциации по формуле
|
|
(7.57) |
В большинстве случаев коэффициент
вариации (![]() )
составляет примерно 1,5 коэффициента
дифференциации (
)
составляет примерно 1,5 коэффициента
дифференциации (![]() ),
т.е.
),
т.е.
|
|
(7.58) |
Если сопоставляются 9-я (
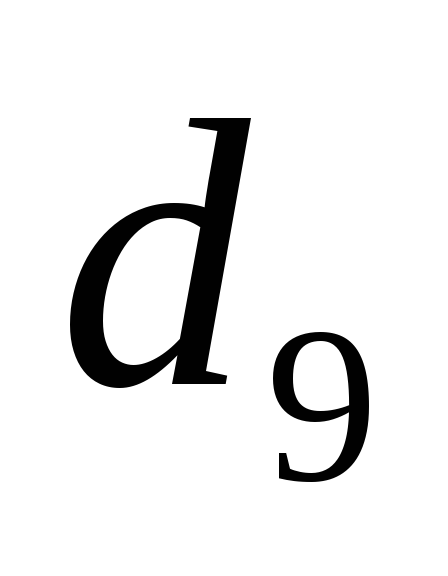 )
и 1-я (
)
и 1-я (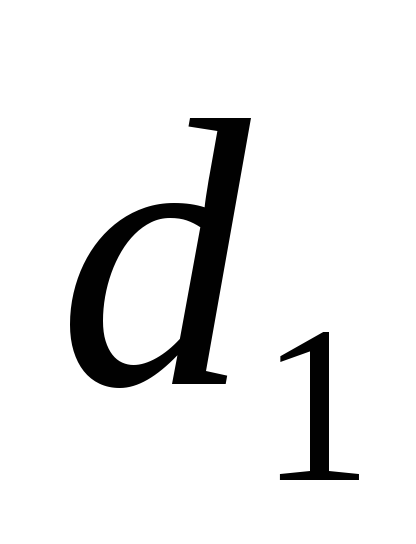 )
децили, тодецилъный коэффициент
дифференциации (
)
децили, тодецилъный коэффициент
дифференциации (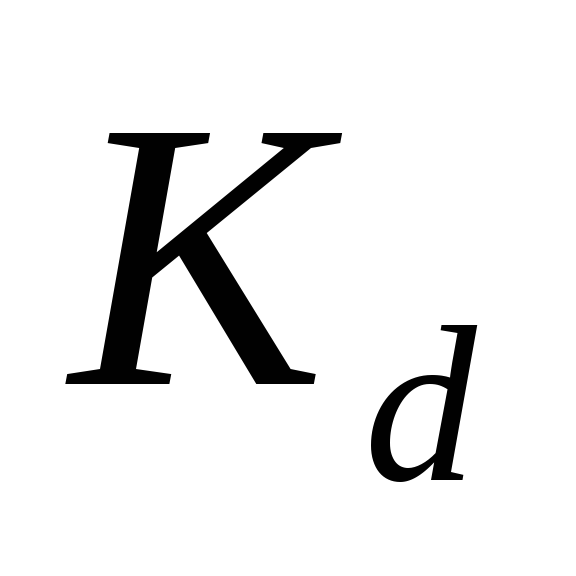 )
вычисляется по формуле:
)
вычисляется по формуле:
|
|
(7.59) |
Рассмотренный выше показатель дифференциации не совсем точно измеряет уровень дифференциации, так как сопоставляется минимальная величина признака (25% или 10% самых крупных единиц совокупности) с максимальной величиной признака (25% или 10% самых мелких единиц совокупности).
Более точно уровень дифференциации можно измерить, сопоставив средние уровни, полученные из 10% наибольших и наименьших значений признака в совокупности. Такой показатель называется коэффициентом фондовой дифференциации (
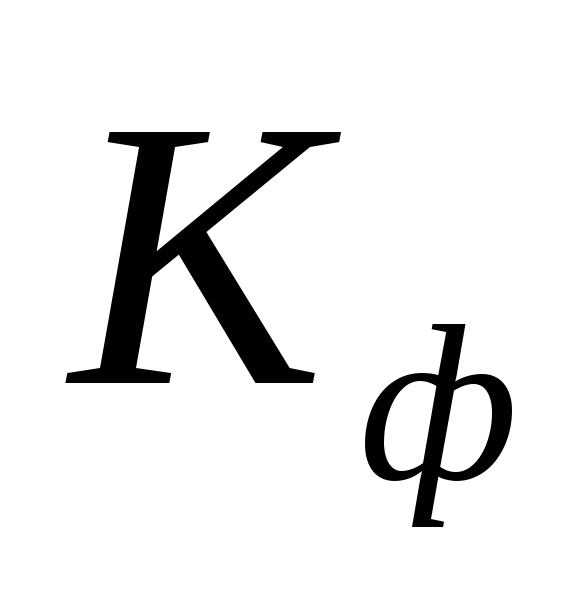 ).
).
|
|
(7.60) |
где
![]() - сумма значений признака 10% самых крупных
единиц в совокупности;
- сумма значений признака 10% самых крупных
единиц в совокупности;
![]() - число единиц совокупности самых крупных
и мелких;
- число единиц совокупности самых крупных
и мелких;
![]() - сумма значений признака 10% самых мелких
единиц в совокупности.
- сумма значений признака 10% самых мелких
единиц в совокупности.
7.7 Моменты распределения
Для подробного описания особенностей распределения используются дополнительные характеристики, в частности, определяются моменты распределения. Способ моментов был разработан русским математиком П.Л. Чебышевым и успешно применен А.А. Марковым для рассмотрения возможностей использования закона нормального распределения при изучении сумм большого, но конечного числа независимых случайных величин.
Моментом
![]() -го
порядканазывается средняя из
-го
порядканазывается средняя из![]() степеней отклонений вариантов
степеней отклонений вариантов![]() от некоторой постоянной величины
от некоторой постоянной величины![]() :
:
|
|
(7.61) |
При исчислении средней в качестве весов могут быть использованы частоты, частости или вероятности. При использовании в качестве весов частот или частостей моменты называются эмпирическими, а при использовании вероятностей -теоретическими.
Порядок момента определяется величиной
![]() .Эмпирический момент
.Эмпирический момент
![]() -гопорядка определяется как отношение
суммы произведений
-гопорядка определяется как отношение
суммы произведений![]() степеней отклонений вариантов от
постоянной величины
степеней отклонений вариантов от
постоянной величины![]() на частоты к сумме частот:
на частоты к сумме частот:
|
|
(7.62) |
В зависимости от выбора постоянной
величины
![]() различают три вида моментов:
различают три вида моментов:
-
Начальные моменты (
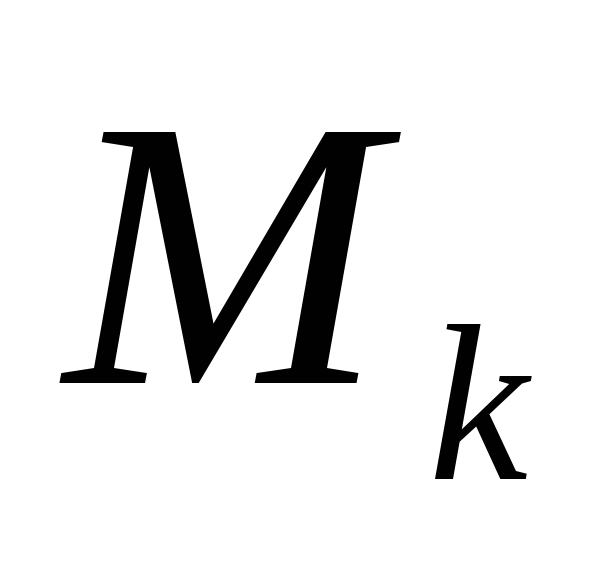 )
получаются, если постоянная величина
)
получаются, если постоянная величина равна нулю (
равна нулю (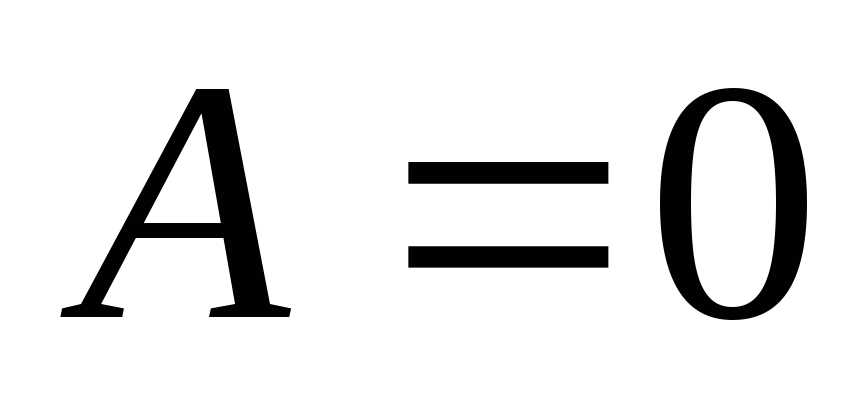 ):
):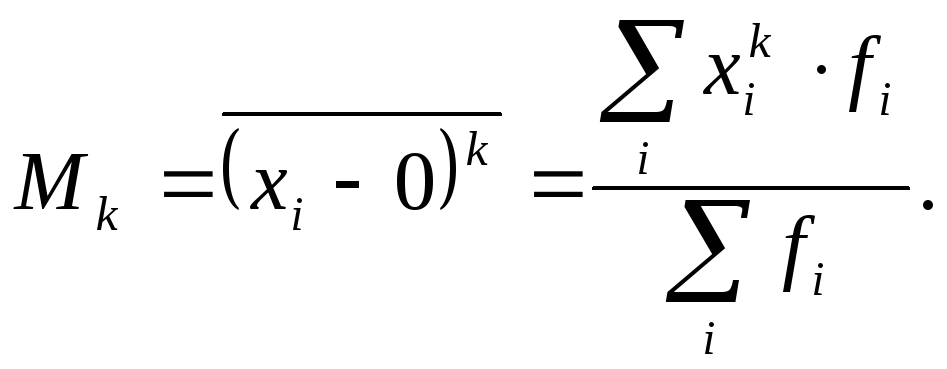
(7.63)
Условные и начальные относительно
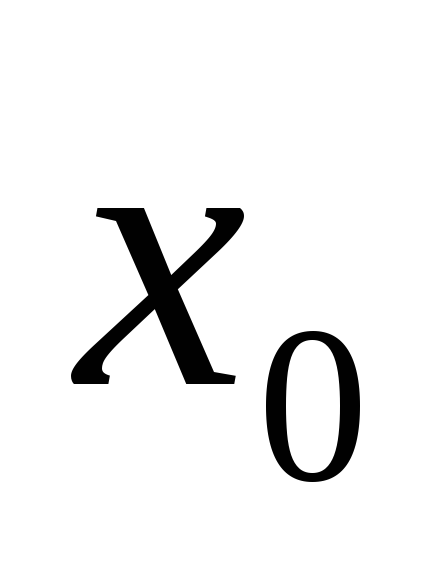 моменты (
моменты (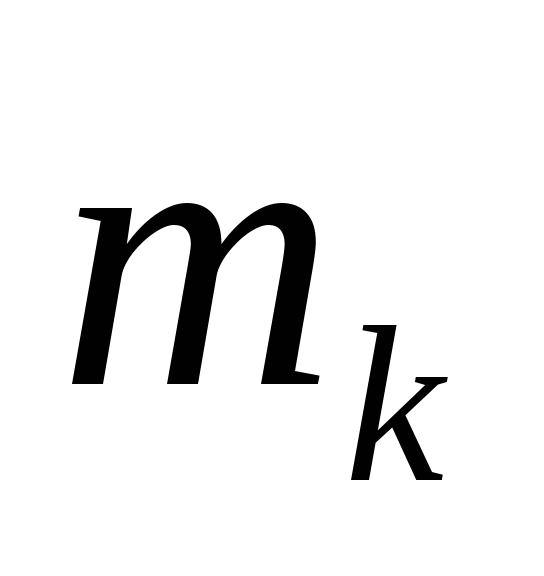 )получаются при
)получаются при равном не нулю, а некоторой производной
величине
равном не нулю, а некоторой производной
величине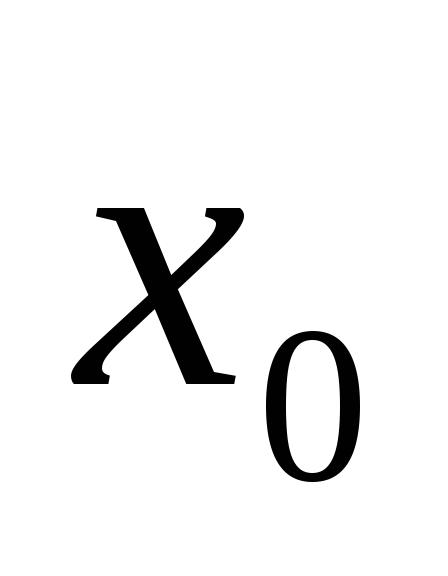 (начало отсчета):
(начало отсчета):
|
|
(7.64) |
С помощью условных моментов упрощается
расчет основных характеристик ряда
распределения. При подстановке различных
значений
![]() получаем начальные моменты относительно
получаем начальные моменты относительно![]() .
Так, например, если
.
Так, например, если
![]() ,
то:
,
то:
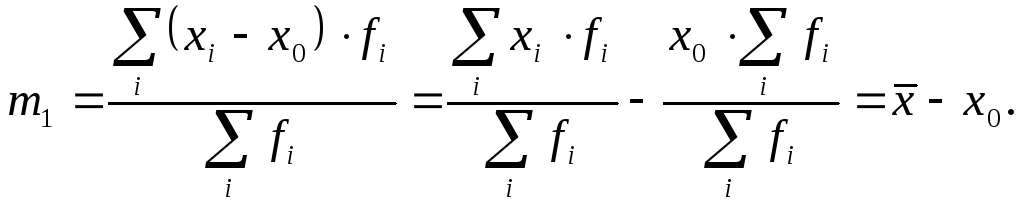
Из этой формулы вытекает, что
![]() ,
т.е. средняя арифметическая равна
началу отсчета плюс начальный момент
первого порядка. Если отклонения
,
т.е. средняя арифметическая равна
началу отсчета плюс начальный момент
первого порядка. Если отклонения![]() имеют общий множитель
имеют общий множитель![]() ,
то на него можно разделить отклонения,
а по окончании вычислить полученный
момент, умножив на этот множитель в
соответствующей степени, т.е.:
,
то на него можно разделить отклонения,
а по окончании вычислить полученный
момент, умножив на этот множитель в
соответствующей степени, т.е.:
|
|
(7.65) |
Отсюда следует, что при
![]()
![]() .
.
Центральные моменты (
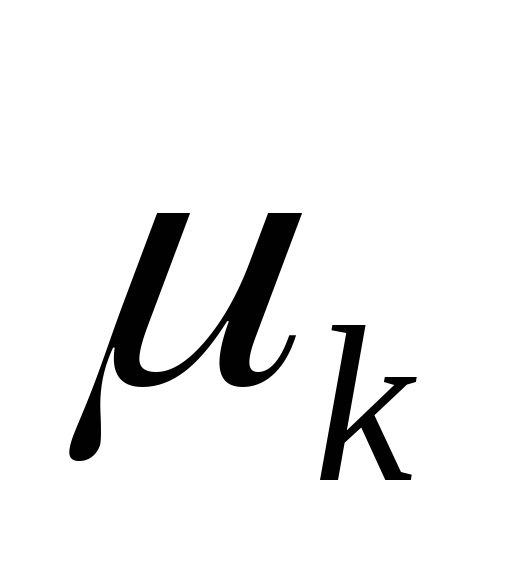 )
получаются, если за постоянную
величину
)
получаются, если за постоянную
величину взять среднюю арифметическую (
взять среднюю арифметическую (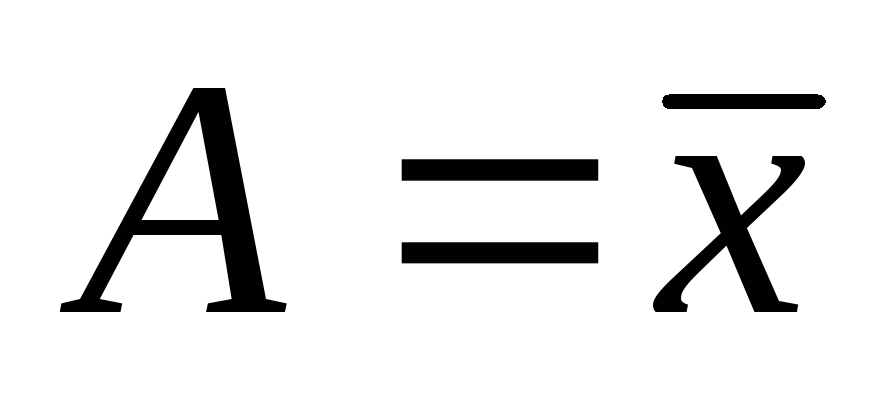 ):
):
|
|
(7.66) |
В статистической практике пользуются в основном моментами 1-го, 2-го, 3-го и 4-го порядков, которые представлены в табл. 7.1.
|
Таблица 7.1 |
|||
|
Виды моментов распределения четырех порядков |
|||
|
Виды моментов
Порядок |
Начальные |
Центральные |
Условные |
|
1-й |
|
|
|
|
2-й |
|
|
|
|
3-й |
|
|
|
|
4-й |
|
|
|