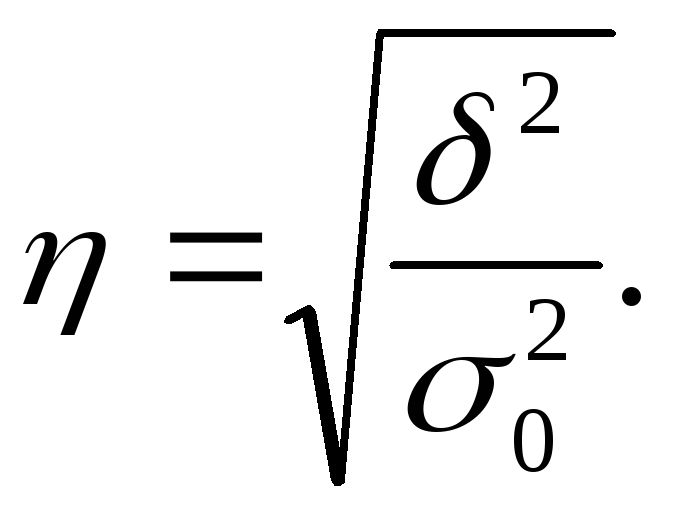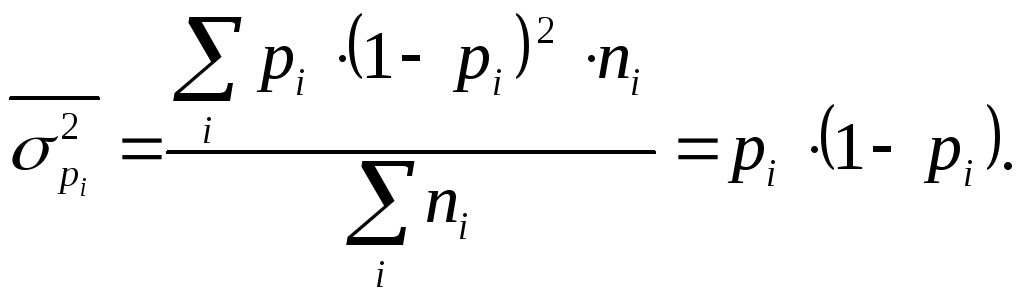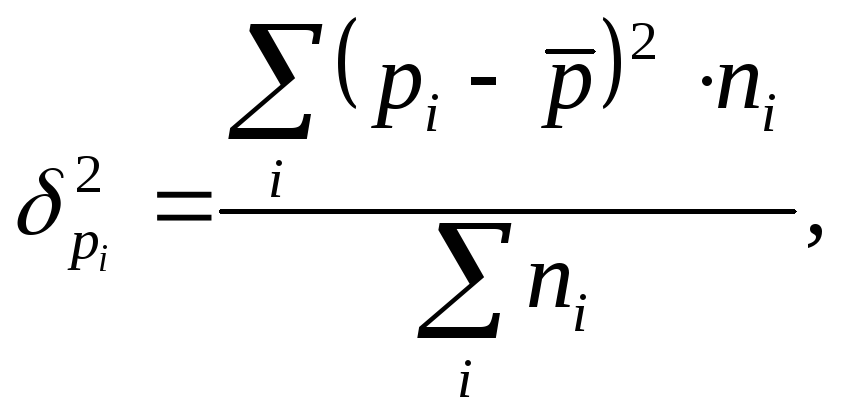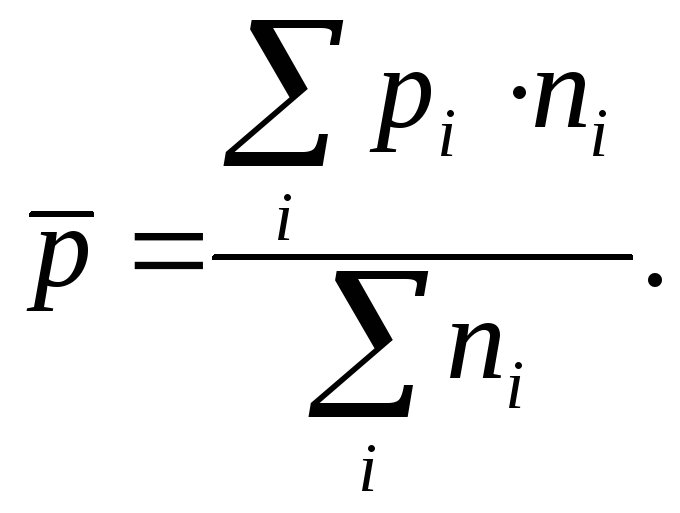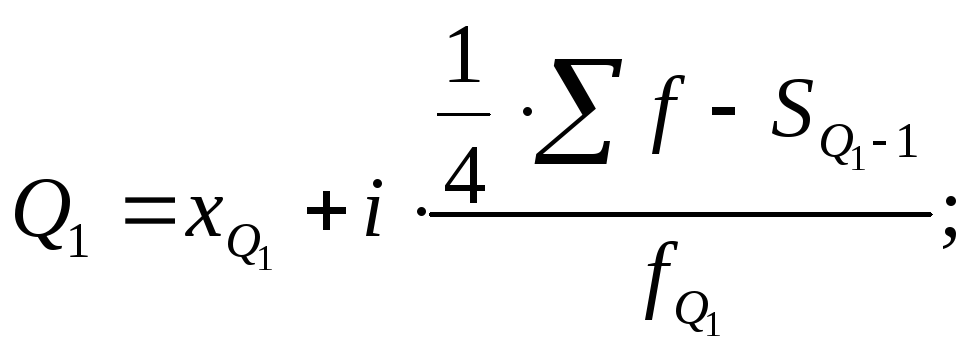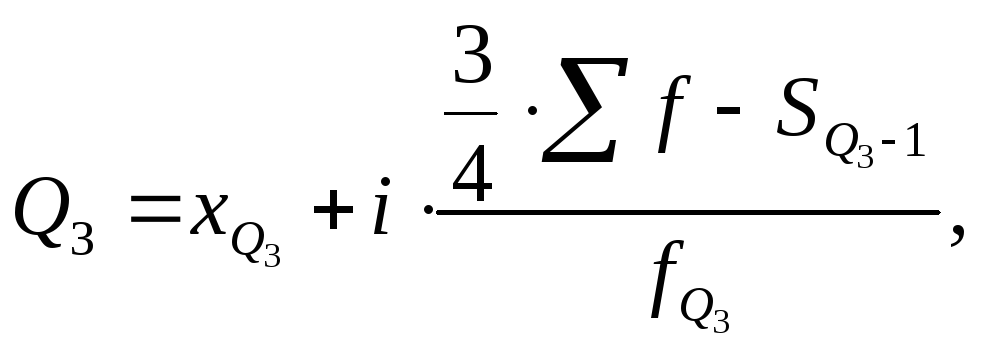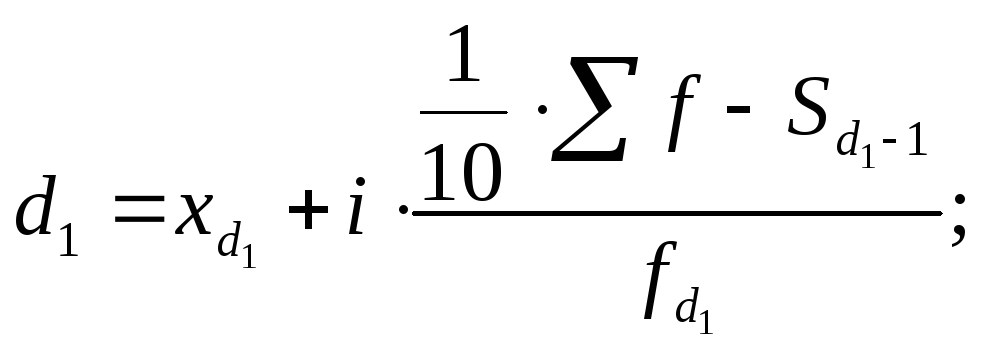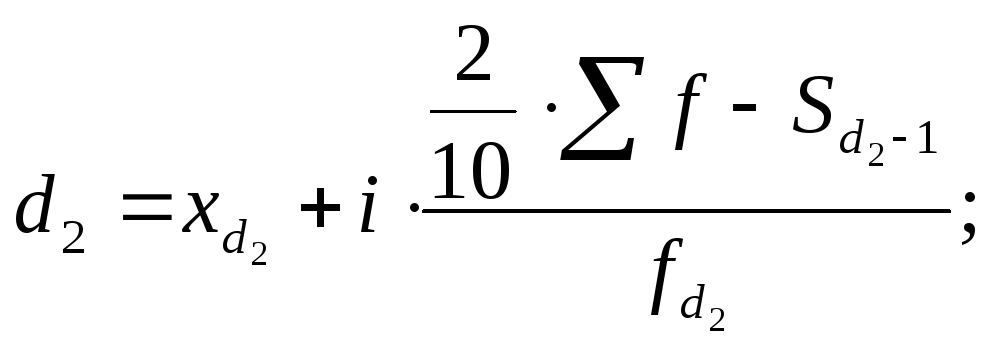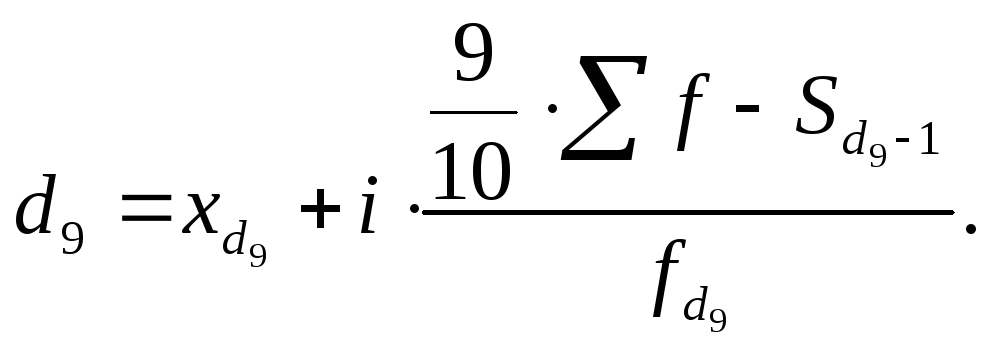Файл: Тема 7.doc

(7.43)

Это отношение характеризует влияние признака, положенного в основание группировки, на вариацию результативного признака. Эмпирическое корреляционное отношение изменяется в пределах от 0 до 1. Если , то группировочный признак не оказывает влияния на результативный. Если, то результативный признак изменяется только в зависимости от признака, положенного в основание группировки, а влияние прочих факторных признаков равно нулю. Промежуточные значения оцениваются в зависимости от их близости к предельным значениям.

Для проверки существенности связи между группировочным признаком и вариацией исследуемого признака часто используется дисперсионное отношение (критерий Фишера).

(7.44)

где и- число степеней свободы для сравниваемых дисперсий, при этом;;

- число групп;

- число наблюдений.

Расчетное значения критерия Фишера () сравнивается с критическим(), которое определяется по таблице приложения 4 в зависимости от числа степеней свободы и уровня значимости. Если, наличие связи доказано, так как проверяется нулевая гипотеза об отсутствии взаимосвязи признаков, т.е. об отсутствии влияния группировочного признака на исследуемый признак.

---

Правило сложения дисперсий для доли признака. Рассмотренное правило сложения дисперсий распространяется и на дисперсии доли признака, т.е. доли единиц с определенным признаком в совокупности, разбитой на группы. При этом изучение вариации происходит непосредственно при вычислении и анализе видов дисперсий для доли признака.

Внутригрупповая дисперсия доли определяется по формуле

(7.45)

где - доля изучаемого признака в отдельных группах.

Средняя из внутригрупповых дисперсий имеет следующий вид:

(7.46)

Формула межгрупповой дисперсии имеет следующий вид:

(7.47)

где - численность единиц в отдельных группах;

- доля изучаемого признака во всей совокупности.

Доля признака в совокупности определяется по формуле средней арифметической взвешенной:

(7.48)

Общая дисперсия определяется по формуле

(7.49)

Три вида рассмотренных дисперсий связаны между собой следующим образом:

(7.50)

Это соотношение дисперсий называется правилом сложения дисперсий доли признака.

---

Зная любые два вида дисперсий из трех, входящих в формулу (7.50), можно определить дисперсию третьего вида или проверить правильность ее расчета.

---

7.6 Структурные характеристики вариационного ряда распределения. Показатели дифференциации

Рассмотренные обобщающие показатели центра распределения и степени вариации не дают понятия о форме распределения, т.е. не вскрывают характера последовательного изменения частот. Для выражения особенностей формы распределения применяются показатели дифференциации, основанные на структурных (ранговых) показателях распределения.

Структурные показатели. В системе структурных показателей в качестве показателей особенностей формы распределения выступают варианты, занимающие определенное место (каждое четвертое, пятое, десятое, двадцать пятое и т.д.) в ранжированном вариационном ряду. Такие показатели носят общее названиеквантилей, илиградиентов.

Некоторые квантили имеют особые наименования: квартили, квинтили, децили и перцентили.

Квартили представляют собой значение признака, делящее ранжированную совокупность на четыре равновеликие части. Различают квартиль нижний (), отделяющийчасть совокупности с наименьшими значениями признака, и квартиль верхний (), отсекающийчасть с наибольшими значениями признака. Это означает, что 25% единиц совокупности будут меньше по величине; 25% единиц будут заключены междуи; 25% - междуии остальные 25% превзойдут. Вторая квартиль является медианой. Вычисление квартилей аналогично вычислению медианы.

Для расчета квартилей по интервальному вариационному ряду используются формулы

	(7.51)
	(7.52)

---

где - нижняя граница интервала, содержащего нижний квартиль (интервал определяется по накопленной частоте, первой превышающей 25%);

- нижняя граница интервала, содержащего верхний квартиль (интервал определяется по накопленной частоте, первой превышающей 75%);

- величина интервала;

- накопленная частота интервала, предшествующего интервалу, содер­жащему нижний квартиль;

- то же для верхнего квартиля;

- частота интервала, содержащего нижний квартиль;

- то же для верхнего квартиля.

Квинтили делят распределение на пять равных частей.

Децили () - это значения вариант, которые делят ранжированный ряд на десять равных частей: 1-й дециль () делит совокупность в соотношениик,2-й дециль () - в соотношениики т.д.

Вычисляются децили по той же схеме, что и медиана, и квартили:

	(7.53)
	(7.54)

и т.д.

(7.55)

---