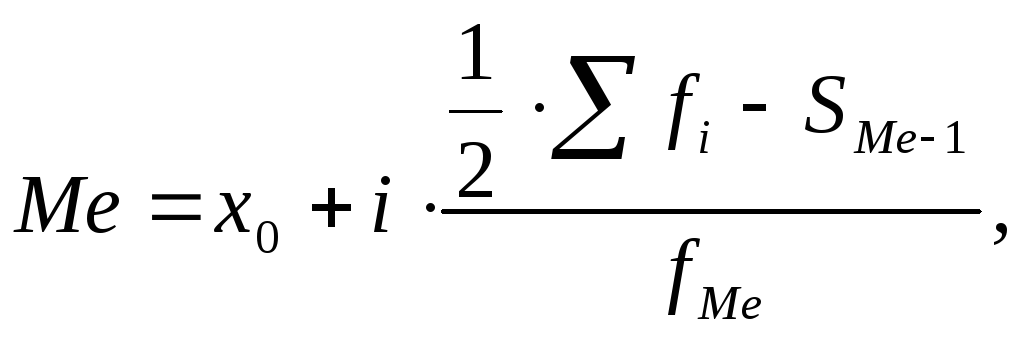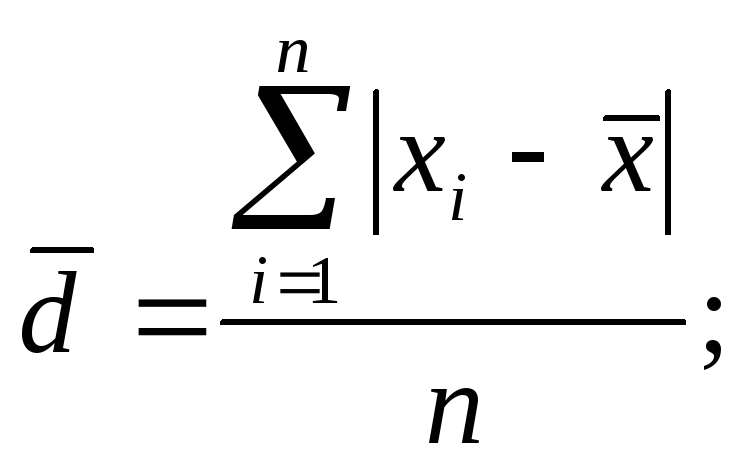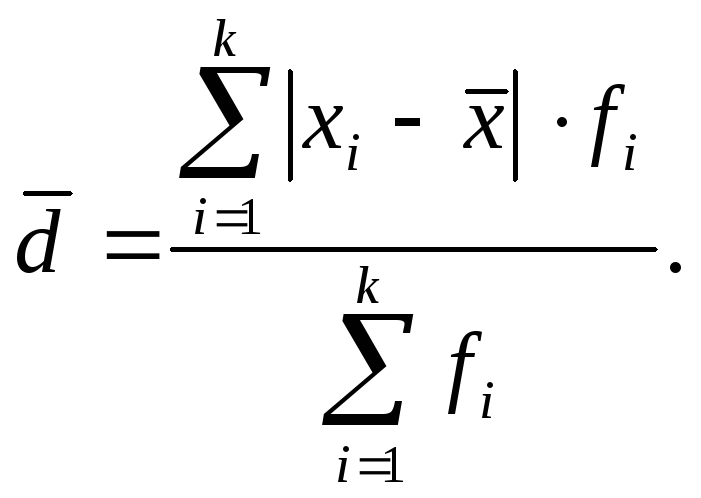ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.08.2024
Просмотров: 111
Скачиваний: 0
СОДЕРЖАНИЕ
Тема 7 показатели вариации и анализ частотных распределений
Вариация признака в совокупности и значение ее изучения
7.2 Показатели центрараспределения
7.3 Показатели вариации и способы их расчета
7.4 Вариации альтернативного признака. Энтропия распределения
7.5 Виды дисперсий в совокупности, разделенной на группы. Правило сложения дисперсий
7.6 Структурные характеристики вариационного ряда распределения. Показатели дифференциации
7.8 Изучение формы распределения
7.9 Теоретические распределения в анализе вариационных рядов
и при четном числе вариантов
|
|
(7.7) |
Если мода отражает типичный, наиболее распространенный вариант значения признака, то медиана практически выполняет функцию средней величины для неоднородной совокупности, не подчиняющейся нормальному закону распределения.
Рассмотрим определение медианы по сгруппированным данным (рядам распределения).
Положение медианы в ряду распределения определяется ее номером:
|
|
(7.8) |
где
![]() - число единиц совокупности.
- число единиц совокупности.
В интервальном ряду распределения сразу можно указать только интервал, в котором будет находиться медиана. Для определения ее величины используется специальная формула:
|
|
(7.9) |
где
![]() - нижняя граница медианного интервала;
- нижняя граница медианного интервала;
![]() - величина медианного интервала;
- величина медианного интервала;
![]() - накопленная частота интервала,
предшествующего медианному;
- накопленная частота интервала,
предшествующего медианному;
![]() - частота медианного интервала.
- частота медианного интервала.
Моду и медиану в интервальном ряду распределения можно определить графически. Мода определяется по гистограмме распределения. Для этого выбирается самый высокий прямоугольник, который в данном случае является модальным. Затем правую вершину модального прямоугольника соединяют с правым верхним углом предыдущего прямоугольника. А левую вершину модального прямоугольника - с левым верхним углом последующего прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось абсцисс.
Абсцисса точки пересечения этих прямых и будет модой распределения (рис. 7.1).

Медиана рассчитывается по кумуляте (рис.7.2). Для ее определения из точки на шкале накопленных частот (частостей), соответствующей 50%, проводится прямая, параллельная оси абсцисс, до пересечения с кумулятой. Затем из точки пересечения указанной прямой с кумулятой опускается перпендикуляр на ось абсцисс. Абсцисса точки пересечения является медианой.

Таким образом, в качестве обобщенной характеристики значений определенного признака у единиц ранжированной совокупности могут быть использованы средняя арифметическая, мода и медиана. Каждая из них имеет свои особенности.
Основной характеристикой центра распределения является средняя арифметическая, для которой характерно то, что все отклонения от нее (положительные или отрицательные) в сумме равняются нулю; для медианы характерно, что сумма отклонений от нее по модулю является минимальной, а мода представляет собой значение признака, которое наиболее часто встречается. Поэтому в зависимости от цели исследования распределения должна выбираться одна из упомянутых характеристик либо же для сравнения вычисляться все три.
Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию.
В симметричных распределениях все три характеристики совпадают. Чем больше расхождение между модой и средней арифметической, тем более асимметричен ряд. Для умеренноасимметричных рядов разность между модой и средней примерно в три раза превышает разность между медианой и средней, т.е.
|
|
(7.10) |
7.3 Показатели вариации и способы их расчета
Средняя величина дает обобщающую характеристику всей совокупности изучаемого явления. Однако, исчислив среднюю арифметическую по данным вариационного ряда, мы еще ничего не знаем о том, как отдельные значения изучаемого признака группируются вокруг средней. В этом отношении наблюдаются существенные различия. В одних случаях отдельные значения признака весьма близки к средней арифметической и мало чем от нее отличаются. В этом случае средняя хорошо представляет всю совокупность. В другом случае, наоборот, отдельные значения далеки от средней, и тогда средняя не будет представлять всю совокупность. Возьмем, например, средний уровень доходов населения. Он может быть исчислен как средняя арифметическая из доходов граждан какой-либо страны. Однако значение средней величины для стран, в которых нет резких различий в уровне доходов, будет гораздо выше, чем для стран, в которых наблюдаются резкие различия.
Поэтому нельзя ограничиться вычислением одной средней величины. Надо изучать не только среднюю, но и отклонения от нее, потому что именно в отклонениях виден весь процесс явления в его диалектическом развитии. Отклонение в одну сторону от средней для некоторых показателей следует рассматривать как ростки нового, отклонения в противоположную сторону - как пережитки старого. Для вариационного ряда важно изучать степень сплоченности всех отдельных значений признака вокруг его среднего значения, степень разбросанности этих значений, степень колеблемости их. Для этого в теории статистики используются показатели вариации.
Показатели вариации делятся на две группы: абсолютные и относительные. К абсолютным показателям относятся: размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение. Котносительным показателям вариации относятся: коэффициенты осцилляции, вариации, относительное линейное отклонение и др. Относительные показатели вычисляются как отношение абсолютных показателей вариации к средней арифметической (или медиане).
Вариационный размах. Вариационный
размах (![]() )
(или, как еще говорят, амплитуда
колебаний) показывает, насколько велико
различие между единицами совокупности,
имеющими самое маленькое и самое большое
значение признака.
)
(или, как еще говорят, амплитуда
колебаний) показывает, насколько велико
различие между единицами совокупности,
имеющими самое маленькое и самое большое
значение признака.
Размах рассчитывают как разность между
наибольшим (![]() )
и-наименьшим (
)
и-наименьшим (![]() )
значениями варьирующего признака, т.е.:
)
значениями варьирующего признака, т.е.:
|
|
(7.11) |
Значение подобного рода величины необходимо в практической и хозяйственной деятельности, а также в научных исследованиях. Например, размах вариации применяется для контроля качества продукции при определении влияния систематически действующих причин на производственный процесс. Для этого через определенные промежутки времени отбирают несколько деталей и проводят их измерение. Рассчитав по данным этих выборок показатели размаха вариации и сопоставив результаты вычислений, судят об устойчивости режима производственного процесса.
В учебной литературе по статистике обычно указывается, что размах имеет существенный недостаток. Его величина всецело зависит от крайних значений признака, и он не учитывает всех изменений варьирующего признака в пределах совокупности. Этот упрек в адрес размаха является не совсем верным. Какой же это недостаток, когда именно в этом заключается суть показателя.
Размах вариации для того и существует, чтобы измерять расстояние между крайними точками. Другое дело, что в изучении вариации нельзя ограничиться определением одного лишь ее размаха. Но это не исключает необходимости определения величины этого показателя, не умаляет его значения.
К действительным недостаткам размаха вариации можно отнести следующее: очень низкое и очень высокое значения признака по сравнению с основной массой его значений в совокупности могут быть обусловлены какими-либо сугубо случайными обстоятельствами, т.е. эти значения являются аномальными в совокупности. В этих случаях размах вариации даст искаженную амплитуду колебания признака против, так сказать, нормальных его размеров, так как в данную совокупность включены единицы другой совокупности с аналогичным признаком. Поэтому прежде чем определить величину размаха вариации, следует очистить совокупность от аномальных наблюдений. Например, нельзя вычислять размах вариации заработков работников какого-либо частного предприятия, если наряду с заработками наемных работников в совокупность включен «заработок» владельца.
Итак, размах вариации - важный показатель колеблемости признака, но он не исчерпывает характеристику вариации.
Среднее линейное отклонение.Для анализа вариации необходим показатель, который бы отражал все колебания варьирующего признака и давал обобщенную его характеристику. Для многих варьирующих признаков возможно допущение, что при прочих равных условиях все единицы совокупности в соответствии с основными законами своего развития имеют одинаковую и при том вполне определенную величину в данных условиях места и времени. Вполне логично в качестве такой величины условно принятьсреднюю величину из всех значений признака, поскольку в ней более или менее погашаются случайные отклонения от закономерного развития явления, и средняя тем самым отражает типичный размер признака у данной однородной совокупности единиц. Но условия существования и развития отдельных единиц совокупности в определенной степени различны, что сказывается на различии значений признака. Средняя величина отражает эти средние условия.
Следовательно, средняя применяется в качестве своего рода центра тяжести, вокруг которого происходит колебание, рассеяние значений признака. При обобщении этих колебаний необходимо прибегать к методу средних величин - искать среднюю величину этих отклонений.
Такая средняя называется средним
линейным отклонением (![]() ).
Эта величина вычисляется как средняя
арифметическая из абсолютных значений
отклонений вариант
).
Эта величина вычисляется как средняя
арифметическая из абсолютных значений
отклонений вариант![]() и
и![]() (простая (формула 7.12) или взвешенная
(формула 7.13), в зависимости от исходных
условий):
(простая (формула 7.12) или взвешенная
(формула 7.13), в зависимости от исходных
условий):
|
|
(7.12) |
|
|
(7.13) |
Поскольку сумма отклонений значений признака от средней величины равна нулю, приходится все отклонения брать по модулю, на что указывают прямые скобки в числителе формул.
Таким образом, среднее линейное отклонение
дает обобщенную характеристику степени
колеблемости признака в совокупности.
Однако при его исчислении приходится
допускать некорректные с точки зрения
математики действия, нарушать законы
алгебры. Математики и статистики искали
иной способ оценки вариации для того,
чтобы иметь дело только с положительными
величинами. Был найден очень простой
выход - возвести все отклонения во вторую
степень. Это столь простое решение
привело в последующем к большим научным
результатам. Оказалось, что обобщающие
показатели вариации, найденные с
использованием вторых степеней
отклонений, обладают замечательными
свойствами; позднее на их основе были
разработаны новые методы исследования,
а также новые показатели количественной
характеристики большого класса явлений.
Полученную меру вариации назвали
дисперсией и обозначили![]() или
или![]() .
.