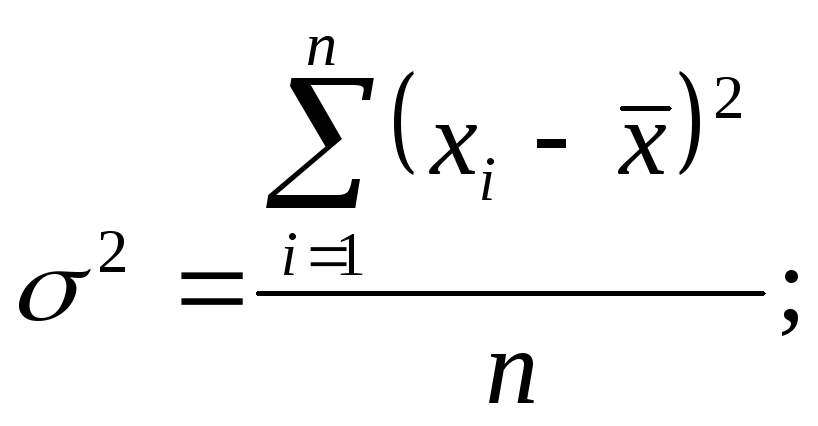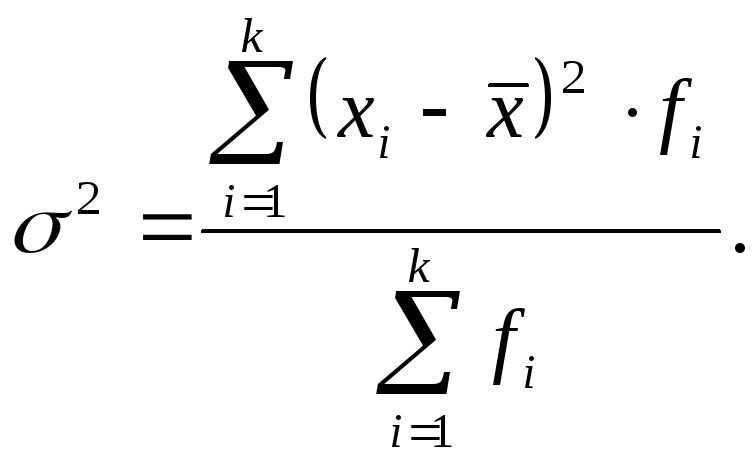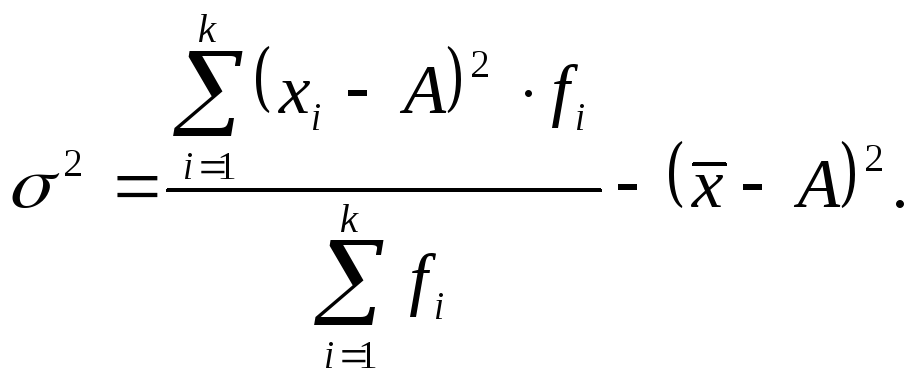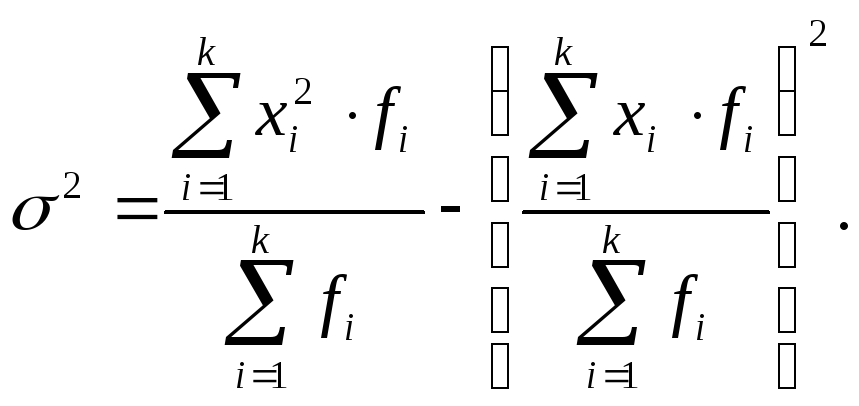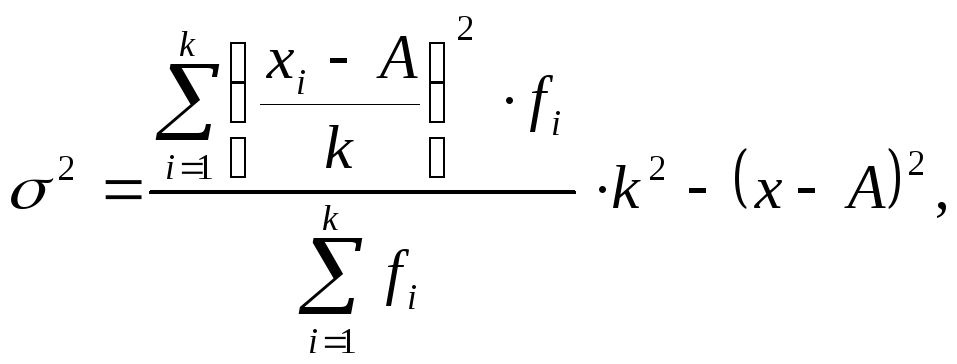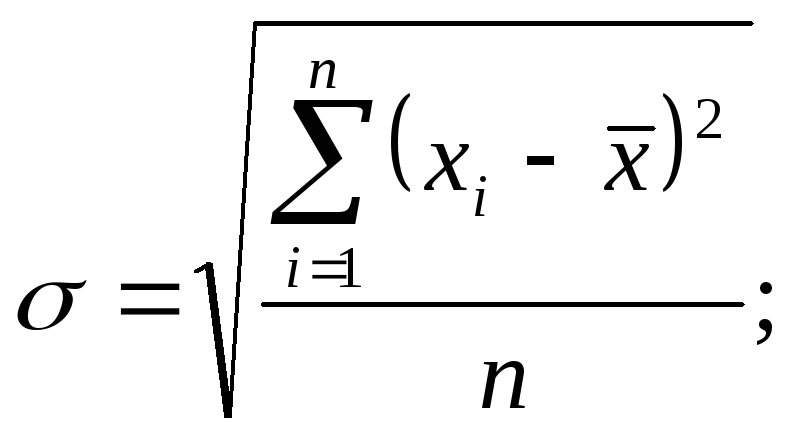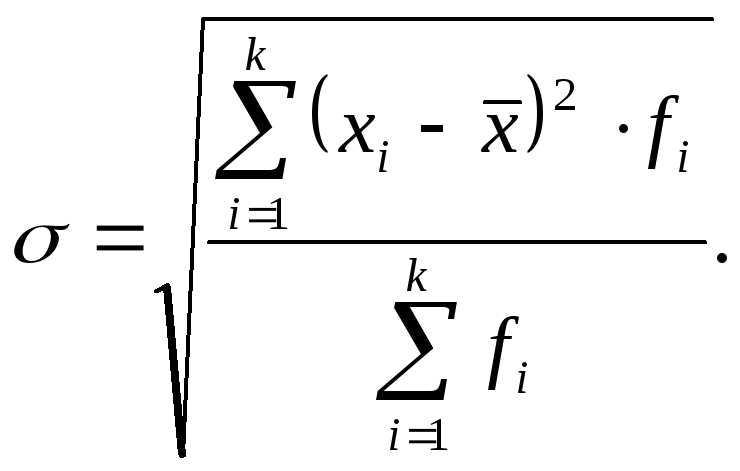ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.08.2024
Просмотров: 123
Скачиваний: 0
СОДЕРЖАНИЕ
Тема 7 показатели вариации и анализ частотных распределений
Вариация признака в совокупности и значение ее изучения
7.2 Показатели центрараспределения
7.3 Показатели вариации и способы их расчета
7.4 Вариации альтернативного признака. Энтропия распределения
7.5 Виды дисперсий в совокупности, разделенной на группы. Правило сложения дисперсий
7.6 Структурные характеристики вариационного ряда распределения. Показатели дифференциации
7.8 Изучение формы распределения
7.9 Теоретические распределения в анализе вариационных рядов
Дисперсия.Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины и в зависимости от исходных данных вычисляется по формулам простой дисперсии (формула 7.14) и взвешенной дисперсии (формула 7.15):
|
|
(7.14) |
|
|
(7.15) |
Расчет дисперсии может быть упрощен. В случае равных интервалов в вариационном ряду распределения используется способ отсчета от условного нуля (способ моментов). Для его понимания необходимо знать математические свойства дисперсии:
Дисперсия постоянной величины равна нулю.
Уменьшение всех значений признака на одну и ту же величину
 не меняет величины дисперсии:
не меняет величины дисперсии:
|
|
(7.16) |
Значит, средний квадрат отклонений можно вычислить не по заданным значениям признака, а по их отклонениям от какого-то постоянного числа.
Уменьшение всех значений признака в
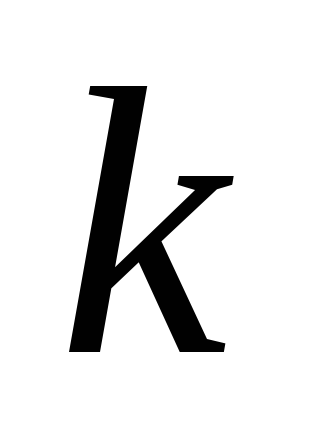 раз уменьшает дисперсию в
раз уменьшает дисперсию в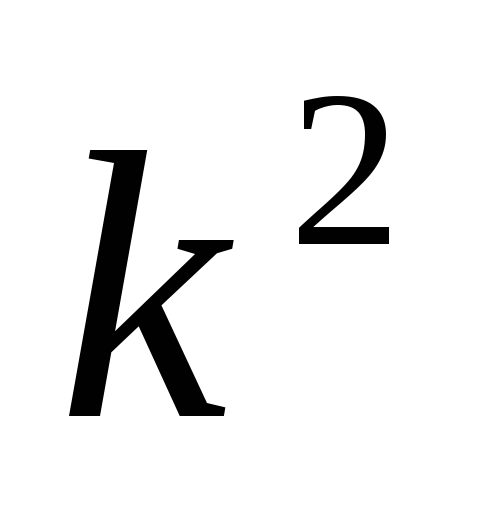 раз, а среднее квадратическое
отклонение - в
раз, а среднее квадратическое
отклонение - в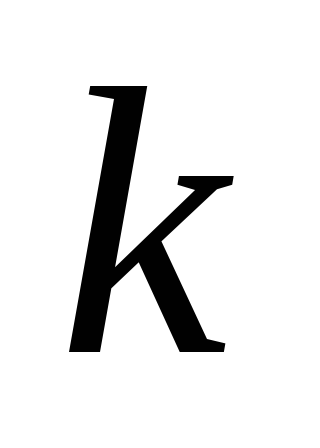 раз:
раз:
|
|
(7.17) |
Значит, все значения признака можно разделить на какое-то постоянное число (скажем, на величину интервала ряда), исчислить среднее квадратическое отклонение, а затем умножить его на, постоянное число:
|
|
(7.18) |
Если исчислить средний квадрат отклонений от любой величины
 ,
в той или иной степени отличающейся
от средней арифметической (
,
в той или иной степени отличающейся
от средней арифметической (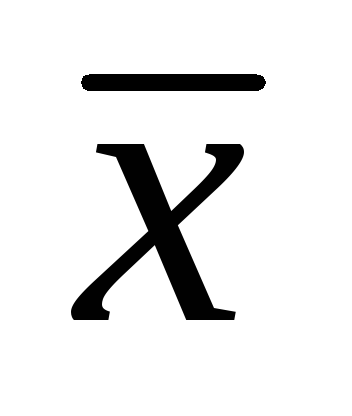 ),
то он всегда будет больше среднего
квадрата отклонений, исчисленного от
средней арифметической:
),
то он всегда будет больше среднего
квадрата отклонений, исчисленного от
средней арифметической:
|
|
(7.19) |
Средний квадрат отклонений при этом
будет больше на вполне определенную
величину - на квадрат разности средней
и этой условно взятой величины, т.е. на
![]() :
:
![]()
или
|
|
(7.20) |
Значит, дисперсия от средней всегда меньше дисперсий, исчисленных от любых других величин, т.е. она имеет свойство минимальности.
В случае когда
![]() приравнивается нулю и, следовательно,
отклонения не вычисляются, формула
принимает такой вид:
приравнивается нулю и, следовательно,
отклонения не вычисляются, формула
принимает такой вид:
![]()
или
|
|
(7.21) |
Значит, средний квадрат отклонений равен среднему квадрату значений признака минус квадрат среднего значения признака.
На приведенных математических свойствах дисперсии основан метод расчета дисперсии по способу моментов, илиспособу отсчета от условного нуля, который применялся при исчислении средней величины. Расчет производится по формуле
|
|
(7.22) |
Где
![]() - ширина интервала;
- ширина интервала;
![]() - условный нуль, в качестве которого
удобно использовать середину интервала,
обладающего наибольшей частотой;
- условный нуль, в качестве которого
удобно использовать середину интервала,
обладающего наибольшей частотой;
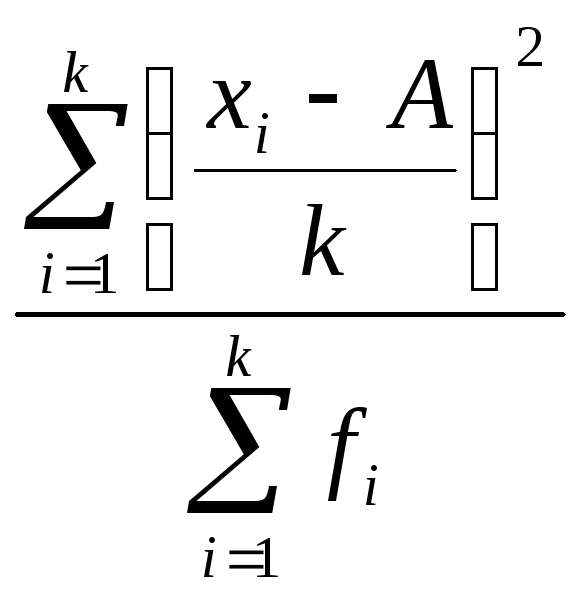 - момент второго порядка.
- момент второго порядка.
Дисперсия есть средняя величина квадратов отклонений, а варианты признака выражены в первой степени.
Среднее квадратическое отклонение (![]() ).
Среднее квадратическое отклонение
равно корню квадратному из дисперсии.
Оно может быть простым (формула 7.23) или
взвешенным (формула 7.24).
).
Среднее квадратическое отклонение
равно корню квадратному из дисперсии.
Оно может быть простым (формула 7.23) или
взвешенным (формула 7.24).
|
|
(7.23) |
или
|
|
(7.24) |
Среднее квадратическое отклонение, как и среднее линейное отклонение, показывает, на сколько в среднем отклоняются конкретные варианты признака от среднего значения. Они выражаются в тех же единицах измерения, что и признак (в метрах, тоннах, рублях и т.д.).
Среднее квадратическое отклонение часто используется в качестве единицы измерения отклонений от средней арифметической. В зарубежной литературе этот показатель называется нормированным, илистандартизованным, отклонением.
По свойству мажорантности средних
величин среднее квадратическое отклонение
всегда больше среднего линейного
отклонения. Если распределение признака
близко к нормальному или симметричному
распределению, то между
![]() и
и![]() существует взаимосвязь:
существует взаимосвязь:![]() или
или![]() .
.
Среднее квадратическое отклонение играет важную роль в анализе вариационных рядов распределения. В условиях нормального распределения существует следующая взаимосвязь между величиной среднего квадратического отклонения и количеством наблюдений:
в пределах
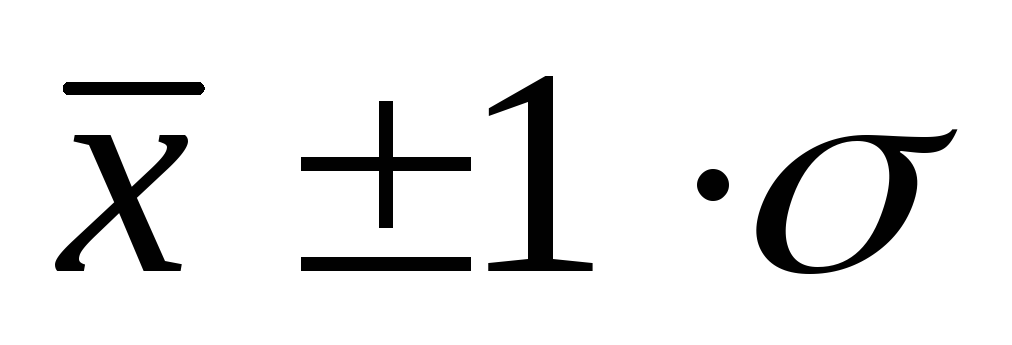 располагается 0,683, или 68,3% количества
наблюдений;
располагается 0,683, или 68,3% количества
наблюдений;в пределах
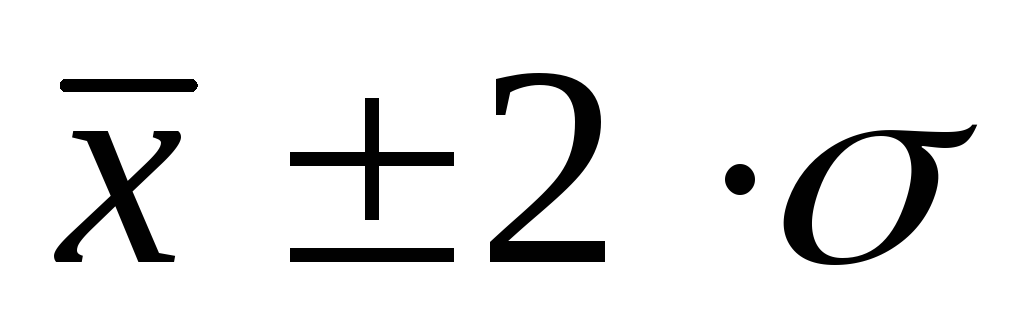 - 0,954, или 95,4%;
- 0,954, или 95,4%;в пределах
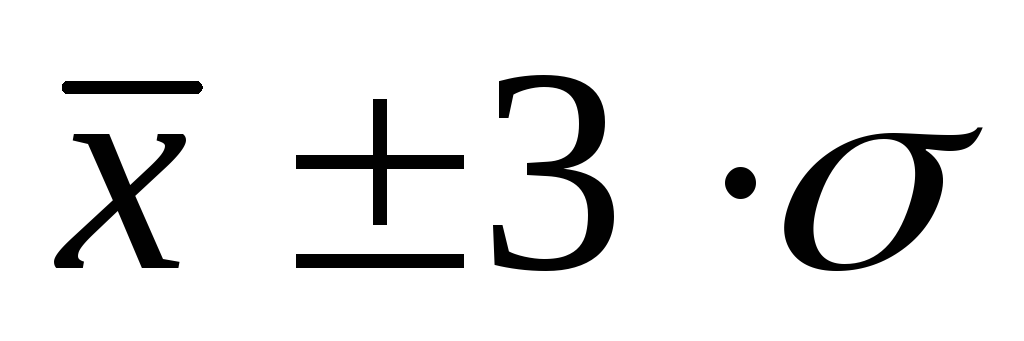 - 0,997, или 99,7% количества наблюдений.
- 0,997, или 99,7% количества наблюдений.
В действительности на практике почти
не встречаются отклонения, которые
превышают
![]() .
Отклонение
.
Отклонение![]() может считаться максимально возможным.
Это положение называютправилом трех
сигм.
может считаться максимально возможным.
Это положение называютправилом трех
сигм.
Для целей сравнения колеблемости различных признаков в одной и той же совокупности или же при сравнении колеблемости одного и того же признака в нескольких совокупностях представляют интерес показатели вариации, приведенные в относительных величинах. Базой для сравнения должна служить средняя арифметическая. Эти показатели вычисляются как отношение размаха вариации, среднего линейного отклонения или среднего квадратического отклонения к средней арифметической или медиане. Чаще всего они выражаются в процентах и определяют не только сравнительную оценку вариации, но и дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному). Различают следующие относительные показатели вариации(V).
Коэффициент осцилляции (![]() ):
):
|
|
(7.25) |
Линейный коэффициент вариации (![]() ):
):
|
|
(7.26) |
или
![]()
Наиболее часто в практических расчетах применяется показатель относительной вариации - коэффициент вариации.
Коэффициент вариации (![]() ):
):
|
|
(7.27) |
Характеристика степени вариации ряда
может быть определена также по формуле
квартильного отклонения (![]() ),
предложенной английским биологом и
антропологом Ф. Гальтоном:
),
предложенной английским биологом и
антропологом Ф. Гальтоном:
|
|
(7.28) |
где
![]() и
и![]() - соответственно 1 -я и 3-я квартили
распределения.
- соответственно 1 -я и 3-я квартили
распределения.
Эта формула дает абсолютный квартильный
показатель вариации. В симметричных
или умеренно асимметричных распределениях![]() .
Так как на квартальное отклонение не
влияют отклонения всех значений признака,
то его использование следует ограничить
случаями, когда определение среднего
квадратического отклонения затруднено
или невозможно. В частности, этот
показатель может быть рекомендован для
рядов распределения с открытыми
интервалами.
.
Так как на квартальное отклонение не
влияют отклонения всех значений признака,
то его использование следует ограничить
случаями, когда определение среднего
квадратического отклонения затруднено
или невозможно. В частности, этот
показатель может быть рекомендован для
рядов распределения с открытыми
интервалами.
В целях сравнения вариации в различных рядах вычисляется относительный квартильный показатель вариации по формуле
|
|
(7.29) |
или
![]()
где
![]() - медиана ряда распределения.
- медиана ряда распределения.