ВУЗ: Смоленский областной казачий институт промышленных технологий и бизнеса
Категория: Методичка
Дисциплина: Методы обработки экспериментальных данных
Добавлен: 29.10.2018
Просмотров: 392
Скачиваний: 10
Пример 1:
Найти графически корни уравнения:
![]() ,
где
,
где
![]()
Решение:
Первый способ:
так как
![]() всегда
положительно, а
всегда
положительно, а
![]() тоже положительно при х>0, то данное
уравнение не имеет положительных корней.
тоже положительно при х>0, то данное
уравнение не имеет положительных корней.
Вычислим значение
функции
![]() для нескольких отрицательных значений
х:
для нескольких отрицательных значений
х:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
То есть при х<х4 разность остается отрицательной, следовательно, ось ОХ мы не пересекаем, и наш искомый корень принадлежит интервалу (0;-1,18), так как в этом интервале функция меняет знак.
![]()
![]()
Точка пересечения графика с осью абсцисс определяет приближенное значение корня
![]()
В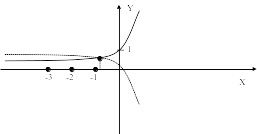 торой
способ:
уравнение записываем в виде
торой
способ:
уравнение записываем в виде
![]() .
Как и ранее, графики функций в левой и
правой части строим по точкам. Построение
следует вести более точно около точки
пересечения:
.
Как и ранее, графики функций в левой и
правой части строим по точкам. Построение
следует вести более точно около точки
пересечения:
Пример 2:
Вычислить с точностью до 0,01 корень
уравнения
![]() =x3-2x2-4x-7=0
на промежутке (3,4)
=x3-2x2-4x-7=0
на промежутке (3,4)
Решение:
1)Используем метод касательных:
Так как
![]() =
-10 ,
=
-10 ,
![]() =
9 (то есть знаки на концах промежутка
различные), то на этом промежутке наша
функция пересекает ось ОХ.
=
9 (то есть знаки на концах промежутка
различные), то на этом промежутке наша
функция пересекает ось ОХ.
Вычислим первую и вторую производные функции:
![]() =3x2-4x-4;
=3x2-4x-4;
![]() =6x-4,
=6x-4,
так как значение обеих производных на (3,4) положительно, то касательную проводим в точке b=4.
Так как
![]() >0,
то
>0,
то
![]() .
.
![]() =1,03;
=1,03;
![]() =21,9;
=21,9;
х2=![]()
Очевидно, что
дальнейшие вычисления не повлияют на
цифру сотен:
![]()
Итак, с точностью большей заданной, х=3,63.
2) Используем метод хорд:
Так как
![]() =
-10 ,
=
-10 ,
![]() =
9 (то есть знаки на концах промежутка
различные), то на этом промежутке наша
функция пересекает ось ОХ.
=
9 (то есть знаки на концах промежутка
различные), то на этом промежутке наша
функция пересекает ось ОХ.
![]() >0
на (3,4), следовательно:
>0
на (3,4), следовательно:
![]() ;
;
![]() Следовательно,
х2(3,53;4)
Следовательно,
х2(3,53;4)
![]() <0
<0
х3(3,62;4)
![]() .
.
Так как х4 отличается от х3 меньше чем на 0,01, значит х3 и есть искомое приближение.
Для проверки:
![]() =0,17>0
=0,17>0 ![]() =-0,04<0.
=-0,04<0.
Задачи
Пользуясь любым из известных методов, определить с точностью до 0,001 корни следующих уравнений:
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
Приложения теории рядов.
Понятие о целях представления сложных для вычислений функций, о точном вычислении «неберущихся» интегралов, о раскрытии неопределенностей, о вычислениях высокоточных значений сложных функций с помощью «карандаша, бумаги и головы», о составлении высокоточных таблиц логарифмов и тригонометрических функций.
Пример:
Разложить в ряд Маклорена функцию
![]() .
.
Решение:
Для нахождения ряда Маклорена вычисляем
значения функции
![]() ,
где n-натуральное
число) и ее производные при х=0:
,
где n-натуральное
число) и ее производные при х=0:
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
Отсюда видно, что:
![]()
![]()
![]()
Подставляем эти значения в ряд Маклорена:
![]()
Получаем:![]()
Найдем радиус сходимости этого ряда:
![]() ;
;
![]()
![]() .
Следовательно, ряд сходится в интервале
(-1,1).
.
Следовательно, ряд сходится в интервале
(-1,1).
Пример 2:
Вычислить
![]() с точностью до 0,01.
с точностью до 0,01.
Решение:
Данный интеграл не выражается в конечном
виде через элементарные функции. Разложим
его подинтегральную функцию в степенной
ряд по формуле:
![]()
Заменим х на (–х)2:
![]()
Отсюда:
![]()
=![]()
Вычисляя члены
этого ряда с точностью до 0,001, замечаем,
что уже шестой член по абсолютной
величине <0,001, значит, надо взять сумму
первых пяти членов, что обеспечивает
требуемую точность:
![]()
Задачи
1. Разложить в ряд
Маклорена
![]()
2. Почленным
интегрированием ряда функции
![]() написать ряд Маклорена для
написать ряд Маклорена для
![]()
![]()
3. Вычислить
![]() с точностью до 0,001
с точностью до 0,001
4. Вычислить
![]() с точностью до 0,0001
с точностью до 0,0001
5. Пользуясь рядами,
вычислить с точностью до 0,0001 интеграл:
![]()
6. Пользуясь рядами,
вычислить с точностью до 0,001 интеграл:
![]()
7. Вычислить sin 10º с точностью до 0,0001
8. Пользуясь рядами,
вычислить с точностью до 0,01 интеграл:
![]()
Найти разложения в ряд Маклорена следующих основных элементарных функций
9.
![]()
10.
![]()
Приближенное вычисление интегралов. 4 часа
Раздел «приближенное вычисление интегралов», а многие студенты, особенно заочного отделения, лишены возможности закрепить полученный ранее на занятиях материал, следует начинать с полуочевидных и легко запоминающихся формул прямоугольников, трапеции, формул Симпсона, затем перейти к интерполяционным полиномам. Заканчивать занятие желательно примерами вычисления центров тяжести или моментов инерции плоских конструкций усложненной геометрии.
Пример 1:
по формулам Симпсона и трапеций вычислить
![]() и сравнить результаты с точным значением
(0,785398).
и сравнить результаты с точным значением
(0,785398).
Решение: Разбиваем сегмент [a,b] на 10 равных частей:
x0 = 0,0 y0=1,0000
x1 =0,1 y1=0,9901
x2 =0,2 y2=0,9615
x3 =0,3 y3=0,9174
x4 =0,4 y4=0,8621
x5 =0,5 y5=0,8000
x6 =0,6 y6=0,7353
x7 =0,7 y7=0,6711
x8 =0,8 y8=0,6098
x9 =0,9 y9=0,5525
x10 =1,0 y10=0,5000
По формуле трапеций:
![]()
По формуле Симпсона:
берем 5 ординат: n=2,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
т.е.
,
т.е.
![]() в 40 раз меньше, чем
в 40 раз меньше, чем
![]() ,
полученное по формуле трапеций.
,
полученное по формуле трапеций.
Задачи
Вычислить интегралы по формуле Ньютона-Лейбница и по приближенным формулам прямоугольников и трапеций и сравнить результаты, если:
1.
![]() ,
при n=6
,
при n=6
2.
![]() ,
при n=8
,
при n=8
3.
![]() ,
при n=8
,
при n=8
4.
![]() ,
при n=4
,
при n=4
5. Выписать формулы для интерполяционного многочлена первой степени.
С помощью формулы Симпсона вычислить следующие интегралы:
6.
![]() ,
при n=4
,
при n=4
7.
![]() ,
при n=6
,
при n=6
8.
![]() ,
при n=6
,
при n=6
9.
![]() ,
при n=8
,
при n=8
10.
![]() ,
при n=4
,
при n=4
Численное дифференцирование.
В теме «численное интегрирование» желательно выделить приложения к «грубым» оценкам, которые необходимы при приближенных инженерных оценках или вычислениях на стадии эскизного проектирования.
Пример 1:
Вычислить приближенно
![]() при
помощи формул численного дифференцирования.
при
помощи формул численного дифференцирования.
Решение:
Воспользуемся формулой
![]() .
.
Получим:
![]() .
.
Пусть х0 = 27, тогда h = -1:
![]()
Пример 2: Вычислить ln1,05
Решение: возьмем х0 = 1, h=0,05, тогда:
![]()
![]()
Задачи
Вычислить при помощи формул численного дифференцирования приближенное значение:
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6. cos 606
7.
![]()
8.
![]()
9.
![]()
10. cos 596.