Добавлен: 19.10.2018
Просмотров: 7805
Скачиваний: 114
СОДЕРЖАНИЕ
Форматирование деловых документов
Лабораторная работа №3 Шаблоны писем, рассылки
«Почтовая рассылка и распечатка бланков Word с данными из Excel»
Выпадающий список с наполнением в электронных таблицах Excel
Веб-опрос с помощью Excel и SkyDrive
Шаг 1. Создаем опрос в SkyDrive
Шаг 3. Публикация опроса и сбор данных
Проектная диаграмма Ганта с помощью условного форматирования
Лабораторная работа №7. Деловая графика Интерактивная диаграмма
Шаг 1. Создаем дополнительную таблицу для диаграммы
Шаг 2. Добавляем флажки (checkboxes) для валют
Шаг 3. Транслируем данные в дополнительную таблицу
Шаг 4. Создаем полосы прокрутки для оси времени и масштабирования
Шаг 5. Создаем динамический именованный диапазон
Анализ детализации мобильной связи (Билайн)
Постановка задачи для принятия решения.
Создание инфологической и логической моделей базы данных.
Создание реляционной базы данных.
Создание форм для ввода данных в таблицы.
Лабораторная работа №11. Формирование сложных запросов
Лабораторная работа № 12. Создание сложных форм и отчетов
Лабораторная работа № 13 Заполнение бланков данными из таблицы
Шаг 2. Подготовка таблицы платежей
Шаг 3. Связываем таблицу и бланк
Шаг 4. Чтобы не было двух "х"...
Лабораторная работа № 16 Защита данных в Microsoft Excel
Уровень 0. Защита от ввода некорректных данных в ячейку
Уровень 1. Защита ячеек листа от изменений
Уровень 2. Выборочная защита диапазонов для разных пользователей
Лабораторная работа № 9. Оптимизация бизнес-модели
-
Работа с дополнением Пакет анализа Подбор параметра.
Цель занятия: изучение технологии подбора параметра при обратных расчетах.
Подбор параметра — это способ прогнозирования значения с помощью анализа «что – если»
Когда желаемый результат одиночной формулы известен, но неизвестны значения, которые требуется ввести для получения этого результата, можно воспользоваться средством Подбор параметра.
С помощью этого средства Microsoft Excel изменяет значение в одной конкретной ячейке до тех пор, пока формула, зависимая от этой ячейки не возвращает нужный результат
Такая задача встречается довольно часто. Есть некоторый расчет. Нужно получить конкретную конечную цифру, изменяя одну из величин, которая участвует в расчетах.
Если требуется найти значение ячейки путем изменения значения только одной другой ячейки, используется команда Подбор параметра (меню Сервис).
Использование операции Подбор параметра в MS Excel позволяет производить обратный расчет. Задается конкретное значение рассчитываемого параметра. По этому значению подбирается некоторое, удовлетворяющее заданным условиям, значение исходного параметра расчета. Изменение исходных данных приводит к изменению результатов расчетов.
Задание 1. Используя режим подбора параметра, определить штатное расписания фирмы. Исходные данные приведены на рис. 1
Известно, что в штате фирмы состоит:
-
6 курьеров;
-
8 младших менеджеров;
-
10 менеджеров;
-
3 заведующих отделами;
-
1 главный бухгалтер;
-
1 программист;
-
1 системный аналитик;
-
1 генеральный директор фирмы.
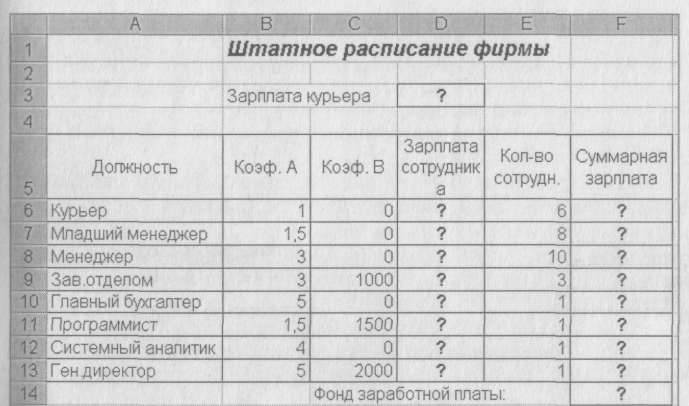
Рис. 1. Исходные данные для Задания
Общий месячный фонд зарплаты составляет 100000 р. Необходимо определить, какими должны быть оклады сотрудников фирмы.
Каждый оклад является линейной функцией от оклада :
зарплатаi = Аi*х + Вi
где х — оклад курьера; Аi и Вi, -коэффициенты, показывающие:
Аi — во сколько раз превышается значение х;
Вi — на сколько превышается значение х.
Действия:
-
Запустить редактор электронных таблиц Microsoft Excel.
-
Открыть файл штатного расписания (штатное_расп.xls).
-
Присвоить имя рабочему листу Подбор параметра
-
Ввести в исходную таблицу данные и формулы.
-
Выделить отдельную ячейку D3 для зарплаты курьера (переменная х).
Все расчеты задать с учетом оплаты курьера. В ячейку D3 временно ввести произвольное число (например, 900 р.).
-
В столбце D ввести формулу для расчета заработной платы по каждой должности. Для ячейки D6 формула расчета имеет вид: = В6 * $D$3 + С6 (ячейка D3 задана в виде абсолютной адресации).
-
Скопировать формулу по столбцу D автокопированием.
-
В столбце F рассчитать заработную плату всех работающих в данной должности. и скопировать формулу по столбцу F автокопированием.
-
В ячейке F14 автосуммированием вычислить фонд заработной платы фирмы.
-
Произвести подбор зарплат сотрудников фирмы для фонда для фонда заработной платы, равной 100000 р.
-
Установить курсор в ячейку F14
-
Активизировать команду пункта меню СервисПодбор параметра.
-
В окне Подбор параметра выполнить:
-
в поле Установить в ячейке окна введите ссылку на ячейку F14 (с формулой расчета фонда заработной платы);
-
в поле Значение набрать искомый результат 100000;
-
в поле Изменяя значение ячейки ввести ссылку на изменяемую ячейку D3 (с значением зарплаты курьера);
-
ОК.
-
Сохранить изменения в электронной книге в своей папке.
-
Записать подобранное значение заработной платы курьера.
-
Распечатать результат в режиме отображения формул.
Анализ задач по заданию 2, 3 показывает, что с помощью MS Excel можно решать линейные уравнения.
Поиск значения параметра формулы — это не что иное, как численное решение уравнений. Другими словами, используя возможности программы MS Excel, можно решать любые уравнения с одной переменной.
Работа с дополнением Пакет анализа. Поиск решения
Цель занятия. Изучение технологии поиска решения для задач оптимизации (минимизации, максимизации).
Задание 2. Выполнить минимизацию фонда заработной платы фирмы.
Известно, что для нормальной работы фирмы требуется от 5 до 7 курьеров, от 8 до 10 младших менеджеров, 10 менеджеров, 3 заведующих отделами, 1 главный бухгалтер, 1 программист, 1 системный аналитик, генеральный директор фирмы.
Общий месячный фонд зарплаты должен быть минимален. Необходимо определить, какими должны быть оклады сотрудников фирмы, при условии, что оклад курьера не должен быть меньше 1400 р.
В качестве модели решения этой задачи применима линейная модель. Условие задачи имеет вид:
N1*А1*х + N2 * (А2*х + В2) + . . . + N8*(А8*х + В8) = Минимум фонда зарплаты,
Где: Ni — количество работников данной специальности;
х — зарплата курьера;
А, и В, — коэффициенты заработной платы сотрудников фирмы.
Действия:
-
Запустить ЭТ MS Excel.
-
Открыть, сохраненный в задании 3, файл штатное_расп.xls
-
Выполнить копию листа Подбор параметра
-
Присвоить копии листа имя Поиск решения
-
Установить курсор в ячейку F14
-
Активизировать команду Поиск решения пункта меню Сервис
-
В окне Поиск решения(рис. 2) выполнить:
-
в поле Установить целевую ячейку указать ячейку F14, (содержащую модель — суммарный фонд заработной платы)
-
активизировать переключатель равной — Минимальному значению (необходимо минимизировать общий месячный фонд зарплаты)
-
в поле Изменяя ячейки указать адреса ячеек, в которых будет отражено количество курьеров и младших менеджеров, а также зарплата курьера — $E$6;$E$7;$D$3 (при задании ячеек Е6, Е7 и D3 следует удерживать клавишу Ctrl).
-
в поле Ограничения, используя кнопку Добавить (открывается окно Добавление ограничений – см. рис. 6.6) описать все ограничения:
|
(зарплата курьера не менее 1400) |
|
|
|
(количество курьеров изменяется от 5 до 7); |
|
||
|
|
(количество младших менеджеров от 8 до 10); |
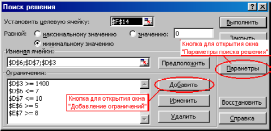
Рис. 2 Окно Поиск решения с заданными условиями для минимизации фонда заработной платы
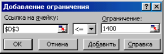
Рис. 3 Окно Добавление ограничений для описания условия: зарплата курьера не менее 1400 р.
После ввода одного условия в окне Добавление ограничений следует активизировать кнопку Добавить.
Завершение ввода условий ограничений и переход в окно Поиск решения осуществляется нажатием кнопки ОК.
8. Ввести параметры поиска, активизировав кнопку Параметры. Параметры установить согласно рис. 4.
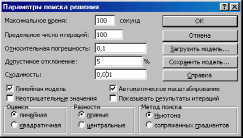
Рис. 4 Задание параметров поиска решения по минимизации фонда зарплаты.
-
Запустить процесс поиска решения нажатием кнопки Выполнить.
-
В открывшемся диалоговом окне Результаты поиска решения установить переключатель Сохранить найденное решение (рис. 5).
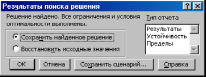
Рис. 5. Сохранение найденного при поиске решения
Решение задачи приведено на рис. 6.. Оно тривиально: чем меньше сотрудников и чем меньше их оклад, тем меньше месячный фонд заработной платы.

Рис. 6. Минимизация
-
Оптимизационные задачи
Предположим, что компания, где вы работаете, имеет два складских помещения, откуда товар поступает в пять ваших магазинов, разбросанных по всей Москве.
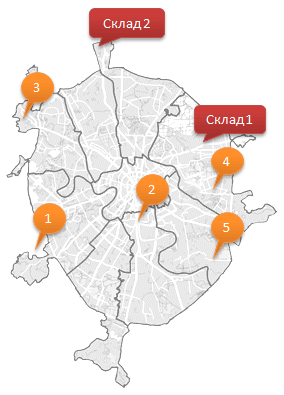
Каждый магазин в состоянии реализовать определенное, известное нам количество товара. Каждый из складов имеет ограниченную вместимость. Задача состоит в том, чтобы рационально выбрать – с какого склада в какие магазины нужно доставлять товар, чтобы минимизировать общие транспортные расходы.
Перед началом оптимизации необходимо будет составить несложную таблицу на листе Excel – нашу математическую модель, описывающую ситуацию:

Подразумевается, что:
-
Серая таблица (B3:G5) описывает стоимость доставки единицы от каждого склада до каждого магазина.
-
Лиловые ячейки (C14:G14) описывают необходимое для каждого магазина количество товаров на реализацию.
-
Красные ячейки (J10:J11) отображают емкость каждого склада – предельное количество товара, которое склад может вместить.
-
Желтые (C12:G12) и синие (H10:H11) ячейки – соответственно, суммы по строке и столбцу для зеленых ячеек.
-
Общая стоимость доставки (E17) вычисляется как сумма произведений количества товаров на соответствующие им стоимости доставки.
Таким образом, наша задача сводится к подбору оптимальных значений зеленых ячеек. Причем так, чтобы общая сумма по строке (синие ячейки) не превышала вместимости склада (красные ячейки), и при этом каждый магазин получил необходимое ему количество товаров на реализацию (сумма по каждому магазину в желтых ячейках должна быть как можно ближе к требованиям – лиловым ячейкам).
Решение
В математике подобные задачи выбора оптимального распределения ресурсов сформулированы и описаны уже давно. И, конечно же, давно разработаны способы их решения. Excel предоставляет пользователю один из них – с помощью мощной надстройки Поиск решения (Solver) , доступной в Excel 2003 через в меню Сервис (Tools) или с вкладки Данные (Data) в новых версиях Excel.
Если в меню Сервис или на вкладке Данные вашего Excel такой команды нет – ничего страшного - значит надстройка просто еще не подключена. Для ее подключения:
-
в Excel 2003 и старше - откройте меню Сервис – Надстройки (Tools – Add-Ins), в появившемся окне установите флажок Поиск решения (Solver) и нажмите ОК. Excel активирует выбранную надстройку и в меню Сервис (Tools) появится новая команда – Поиск решения (Solver).
-
в Excel 2007 и новее - нажать кнопку Офис, далее выбрать Параметры Excel – Надстройки – Перейти (Excel Options - Add-Ins - Go To).
Запустим надстройку. Откроется вот такое окно:
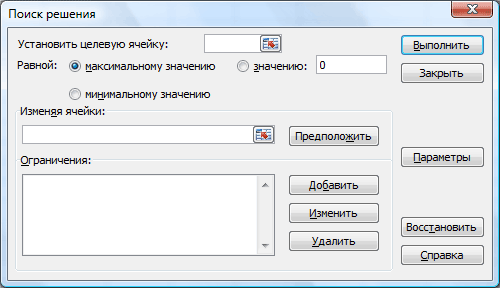
В этом окне нужно задать следующие настройки:
-
Целевая ячейка (Target cell) – тут необходимо указать конечную главную цель нашей оптимизации, т.е. розовую ячейку с общей стоимостью доставки (E17). Целевую ячейку можно минимизировать (если это расходы, как в нашем случае), максимизировать (если это, например, прибыль) или попытаться привести к заданной константе.
-
Изменяемые ячейки (By changing cells) – здесь укажем зеленые ячейки (C10:G11), варьируя значения которых мы хотим добиться нашего результата – минимальных затрат на доставку.
-
Ограничения (Subject to the Constraints) – список ограничений, которые надо учитывать при проведении оптимизации. В нашем случае это ограничения на вместимость складов и потребности магазинов. Для добавления ограничений в список нужно нажать кнопку Добавить (Add) и ввести условие в появившееся окно:
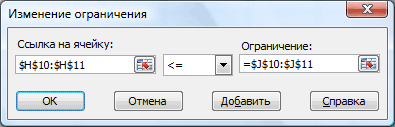
Кроме очевидных ограничений, связанных с физическими факторами (вместимость складов и средств перевозки, ограничения бюджета и сроков и т.д.) иногда приходится добавлять ограничения «специально для Excel». В нашем случае, например, нужно будет добавить вот такое ограничение:

Оно дополнительно уточнит, что объем перевозимого товара (зеленые ячейки) не может быть отрицательным – для человека такое само собой очевидно, но для компьютера это надо прописать явно.
После настройки всех необходимых параметров окно должно выглядеть следующим образом:
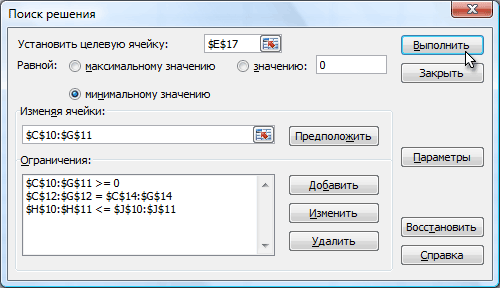
Теперь, когда данные для расчета введены, нажмем кнопку Выполнить (Solve), чтобы начать оптимизацию. В тяжелых случаях с большим количеством изменяемых ячеек и ограничений нахождение решения может занять продолжительное время, но наша задача для Excel проблемы не составит – через пару мгновений мы получим следующие результаты:
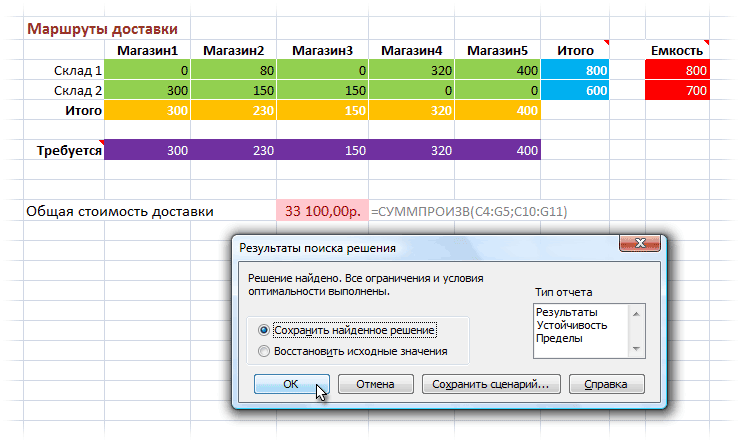
Обратите внимание на то, как интересно распределились объемы поставок по магазинам, не превысив при этом емкости наших складов и удовлетворив все запросы по требуемому количеству товаров для каждого магазина.
Если найденное решение нам подходит, то можно его сохранить, либо откатиться назад к исходным значениям и попробовать еще раз с другими параметрами. Также можно сохранить подобранную комбинацию параметров как Сценарий. По желанию пользователя Excel может построить три типаОтчетов по решаемой задаче на отдельных листах: отчет по результатам, отчет по математической устойчивости решения и отчет по пределам (ограничениям) решения, однако они, в большинстве случаев, интересны только специалистам.
Бывают, однако, ситуации, когда Excel не может найти подходящего решения. Имитировать такой случай можно, если указать в нашем примере требования магазинов в сумме большие, чем общая вместимость складов. Тогда при выполнении оптимизации Excel попытается приблизиться к решению, насколько это возможно, а затем выдаст сообщение о невозможности найти решение. Тем не менее, даже в этом случае мы имеем массу полезной информации – в частности можем видеть «слабые звенья» наших бизнес-процессов и понять направления совершенствования.
Рассмотренный пример, конечно, является относительно простым, но легко масштабируется под решение гораздо более сложных нелинейных задач. Например:
-
Оптимизация распределения финансовых средств по статьям расходов в бизнес-плане или бюджете проекта. Ограничениями, в данном случае, будут являться объемы финансирования и сроки выполнения проекта, а целью оптимизирования – максимизация прибыли и минимизация расходов на проект.
-
Оптимизация расписания сотрудников с целью минимизации фонда заработной платы предприятия. Ограничениями, в этом случае, будут пожелания каждого сотрудника по графику занятости и требования штатного расписания.
-
Оптимизация инвестиционных вложений – необходимость грамотно распределить средства между несколькими банками, ценными бумагами или акциями предприятий с целью, опять же, максимизации прибыли или (если это более важно) минимизации рисков.
В любом случае, надстройка Поиск решения (Solver) является весьма мощным и красивым инструментом Excel и достойна того, чтобы вы обратили на нее свое внимание, поскольку может выручить во многих сложных ситуациях, с которыми приходится сталкиваться в современном бизнесе.